Лекція № 7 Програмовані логічні матриці 1.1 Матрична схема Матрична схема або логічна матриця являє собою сітку ортогональ презентация
Содержание
- 2. З матричної структури шляхом її програмування одержують заданий комбінаційний пристрій. Тому
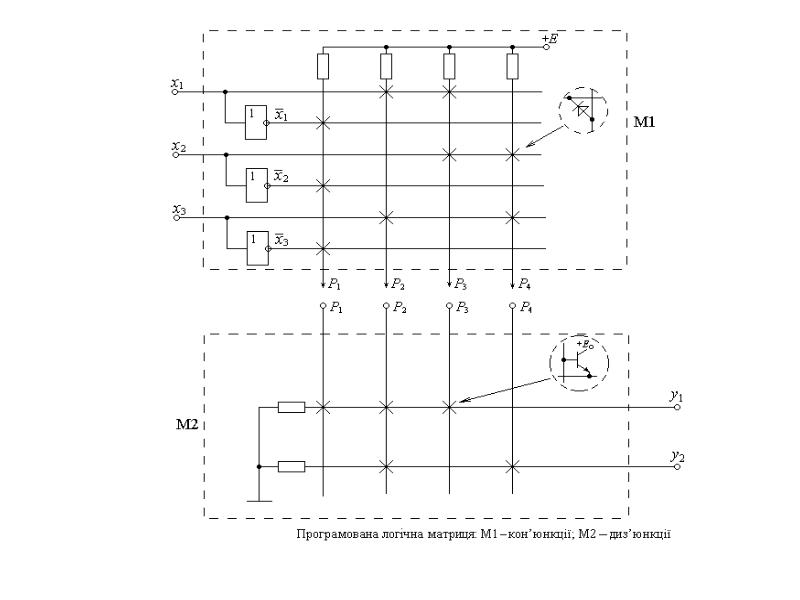
- 4. Таким чином, на вертикальній лінії PN реалізується кон’юнкція змінних. Матриця кон’юнкцій
- 5. Матриця М2 має чотири вертикальні P1 – Р4 шини і дві
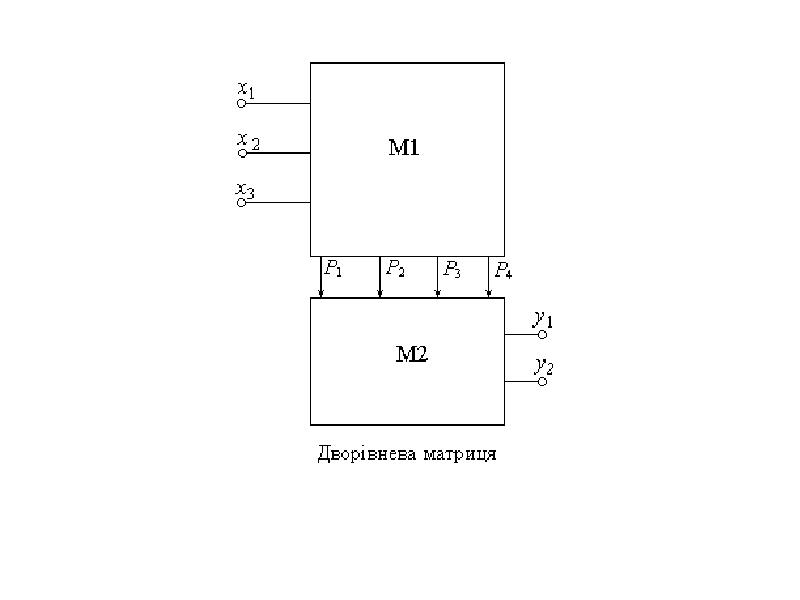
- 6. Якщо з’єднати обидві матриці М1 та М2, то одержана схема буде
- 8. Реалізації системи функцій матрицями М1 та М2 можна зобразити у вигляді
- 9. На перетині j-го рядка і стовпця На перетині
- 10. Складність матричної реалізації оцінюється сумарною ємністю (площею) матриць. У загальному випадку
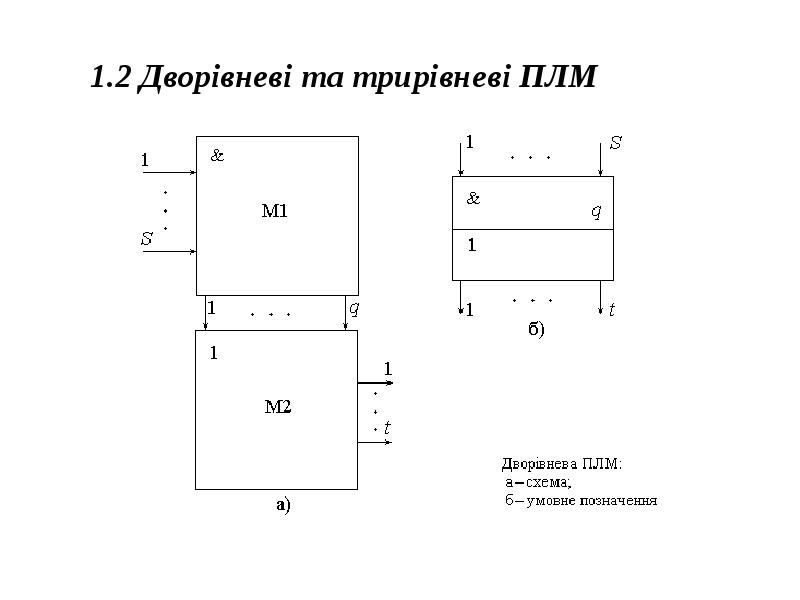
- 11. 1.2 Дворівневі та трирівневі ПЛМ 1.2 Дворівневі та трирівневі ПЛМ
- 12. Матриця М1 має S входів і q виходів. Вона дозволяє реалізувати
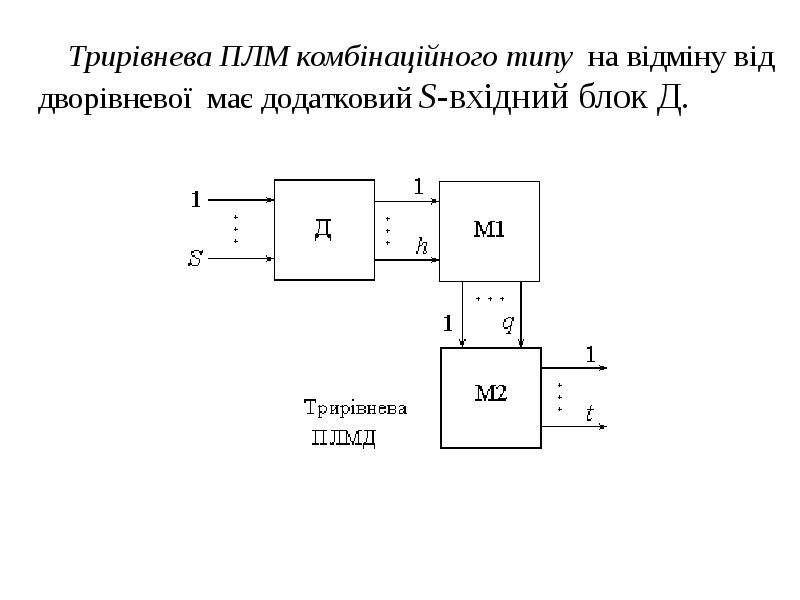
- 13. Трирівнева ПЛМ комбінаційного типу на відміну від дворівневої має додатковий S-вхідний
- 14. Число виходів блока Д дорівнює числу h горизонтальних шин у матриці
- 15. Входи кожного дешифратора – це входи блока Д , а чотири
- 16. Збільшення ефективності використання площі матриць ПЛМ привело до створювання структури, яка
- 17. – на кристалі ВІС ПЛМ передбачена спеціальна система шин, яка дозволяє
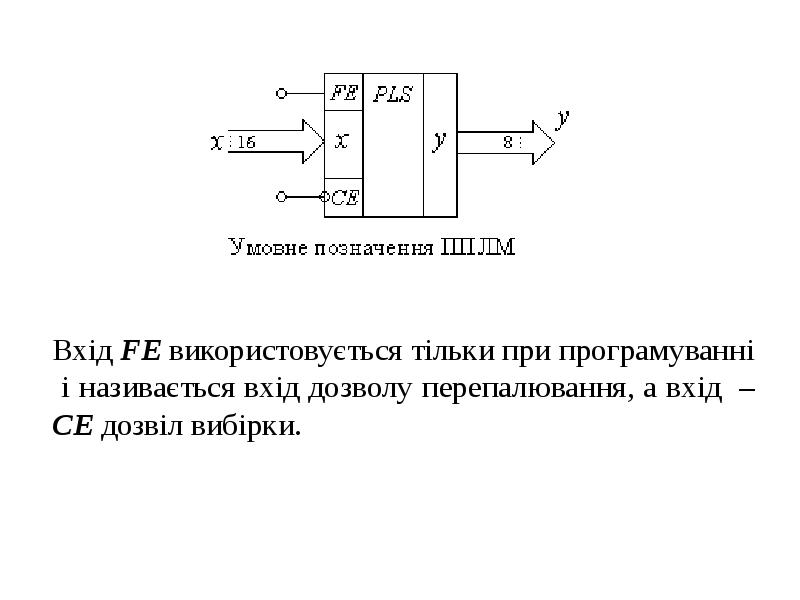
- 18. Перші з них – це мікросхеми, які називають незавершеними логічними матрицями.
- 19. Більш зручними є перепрограмовані ЛМ (ППЛМ). Це стандартні готові мікросхеми –
- 22. Скачать презентацию
















Слайды и текст этой презентации
Скачать презентацию на тему Лекція № 7 Програмовані логічні матриці 1.1 Матрична схема Матрична схема або логічна матриця являє собою сітку ортогональ можно ниже:
Похожие презентации





























