მენეჯერული სტატისტიკა. შერჩევა და შერჩევის განაწილება. თავი 7 презентация
Содержание
- 2. თავის მიზნები თავის შესწავლის შემდეგ თქვენ შეძლებთ: აღწეროთ მარტივი შემთხვევითი
- 3. ბიზნეს სტატისტიკის ინსტრუმენტები აღწერითი სტატისტიკა მონაცემების შეგროვება, წარდგენა და აღწერა დასკვნითი
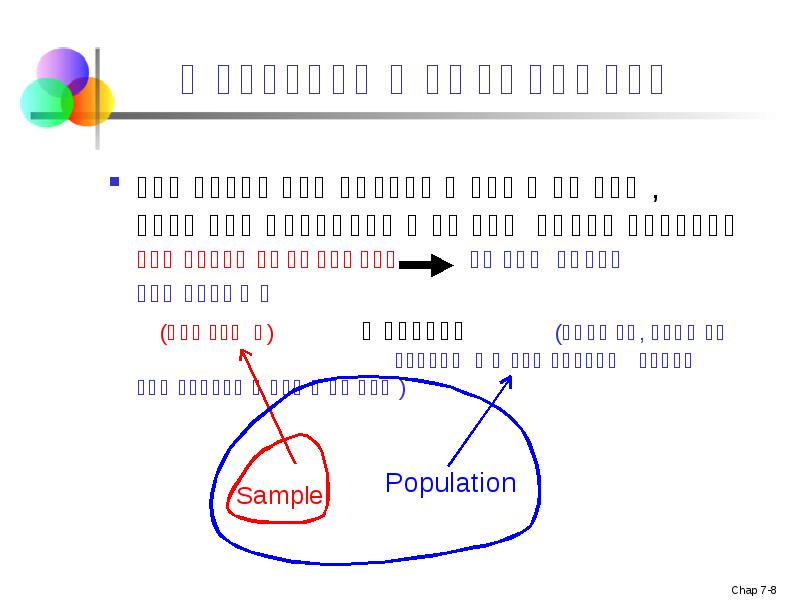
- 4. შერჩევა და პოპულაცია პოპულაცია (Population) არის შესასწავლი ობიექტების (ერთეულების) ყველა შესაძლო
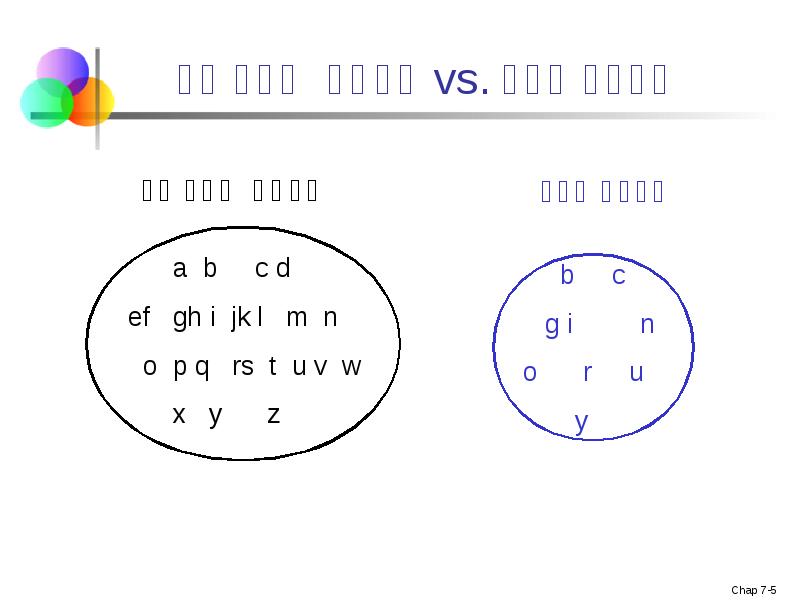
- 5. პოპულაცია vs. შერჩევა
- 6. რატომ შერჩევა? საჭიროებს ნაკლებ დროს ვიდრე პოპულაციის აღწერა საჭიროებს ნაკლებ ხარჯებს
- 7. მარტივი შემთხვევითი შერჩევა პოპულაციის ყველა ობიექტს აქვს შერჩევაში მოხვედრის თანაბარი შანსი
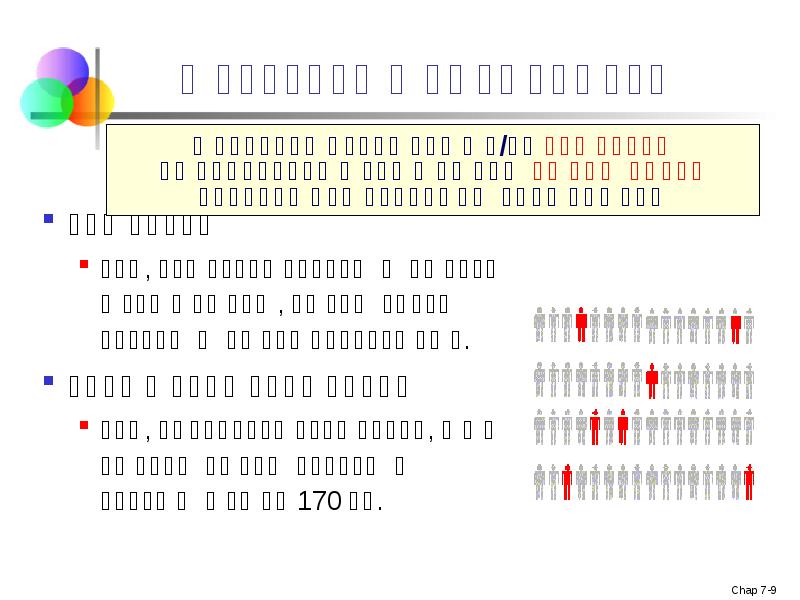
- 8. დასკვნითი სტატისტიკა შერჩევის შედეგებზე დაყრდნობით, აკეთებს განაცხადს პოპულაციის შესახებ შერჩევის სტატისტიკა
- 9. დასკვნითი სტატისტიკა შეფასება მაგ, შერჩევის საშუალო წონაზე დაყრდნობით, პოპულაციის საშუალო წონის
- 10. შერჩევის განაწილება შერჩევის განაწილება არის პოპულაციიდან მიღებული გარკვეული ზომის შერჩევის სტატისტიკის
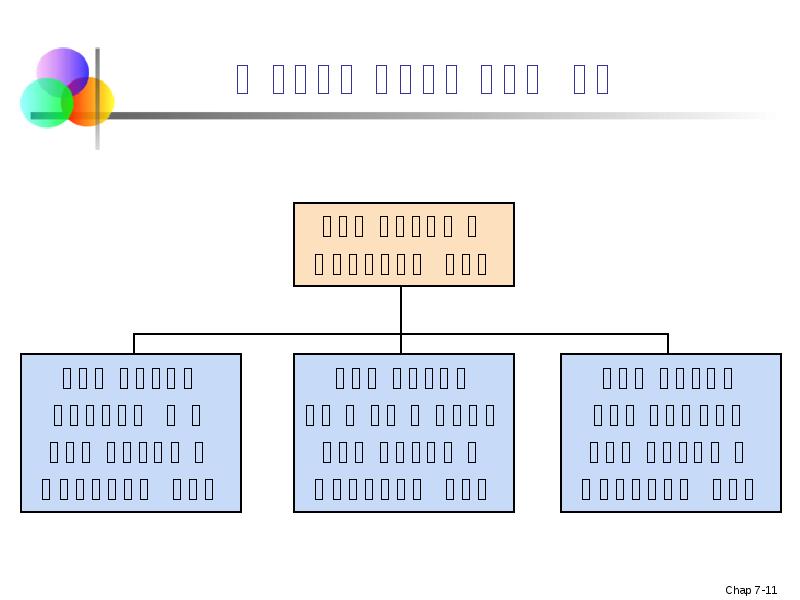
- 11. თავის მიმოხილვა
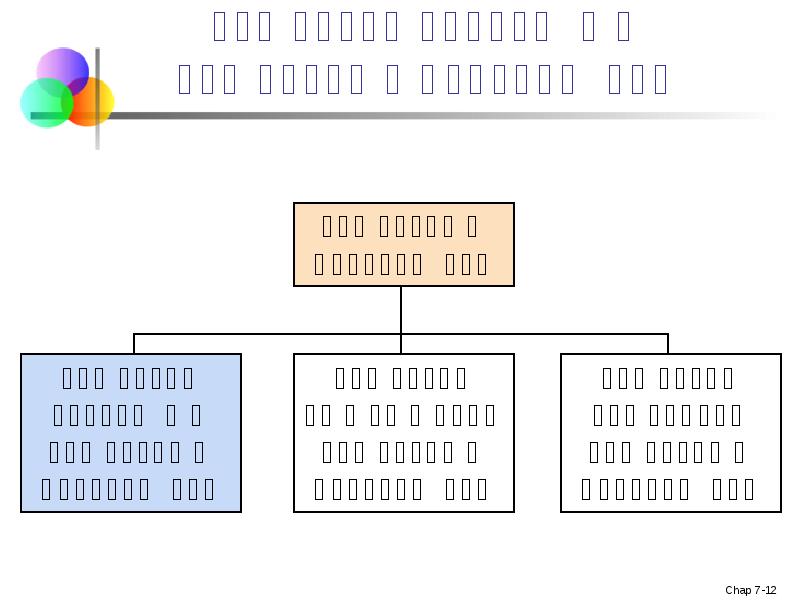
- 12. შერჩევის საშუალოს შერჩევითი განაწილება
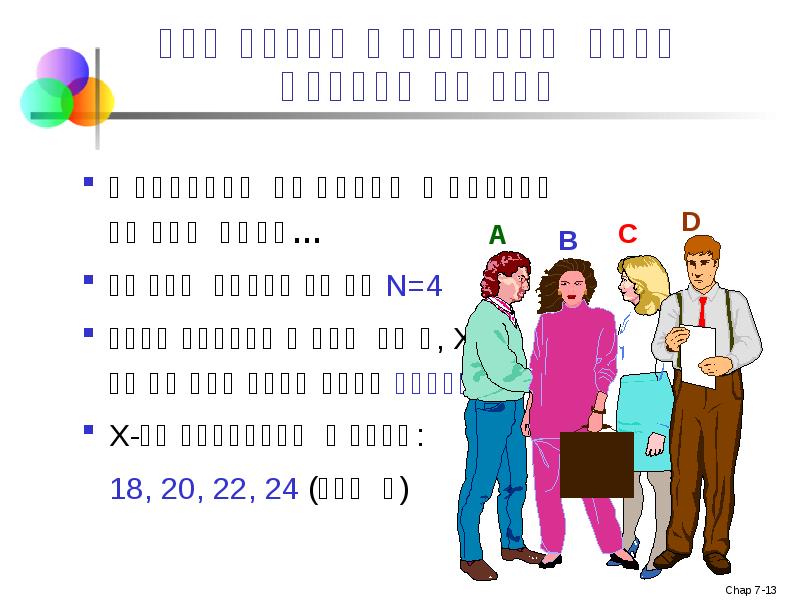
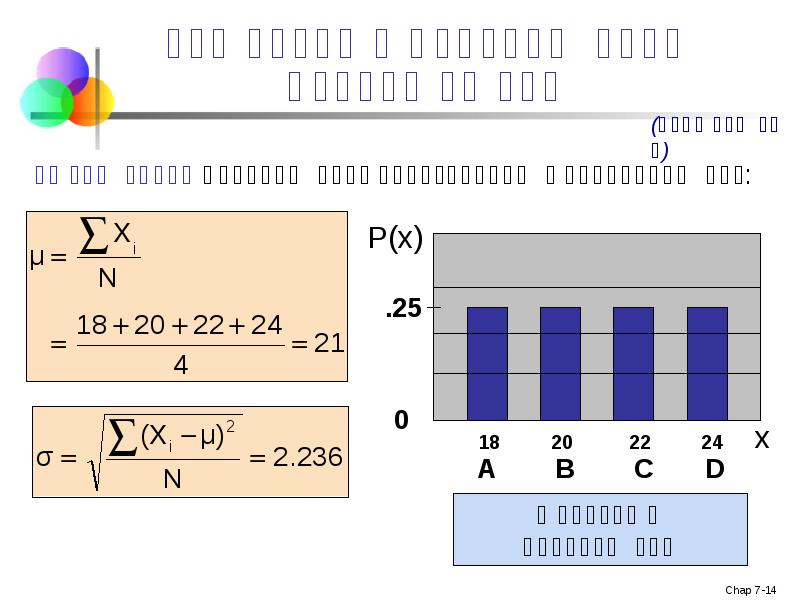
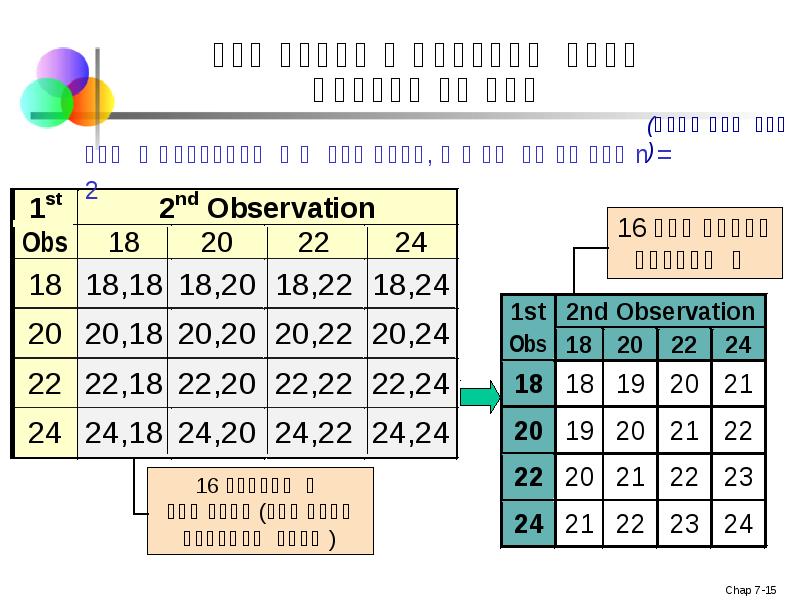
- 13. შერჩევითი განაწილების განვითარება დავუშვათ მოცემული გვაქვს პოპულაცია… პოპულაციის ზომა N=4 შემთხვევითი
- 14. შერჩევითი განაწილების განვითარება
- 15. ახლა განვიხილოთ შერჩევა, რომლის ზომაა n = 2
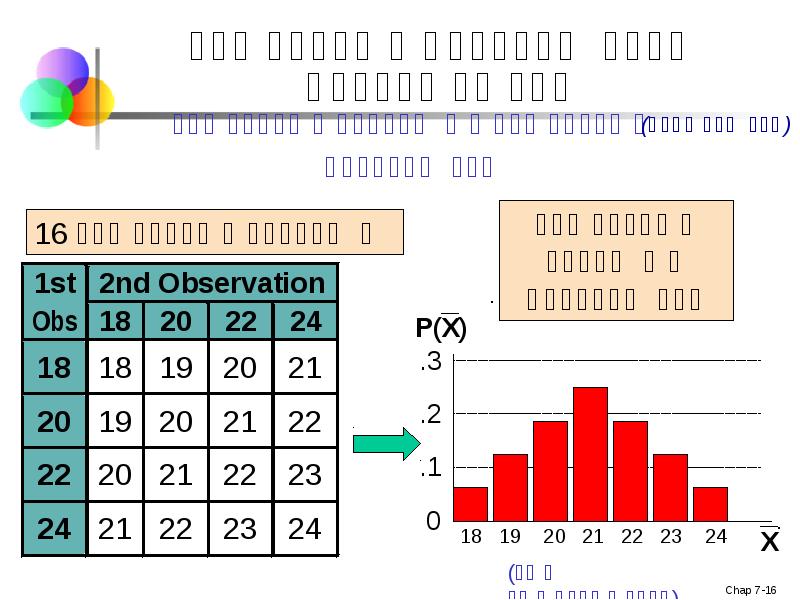
- 16. შერჩევითი საშუალოს შერჩევითი განაწილება
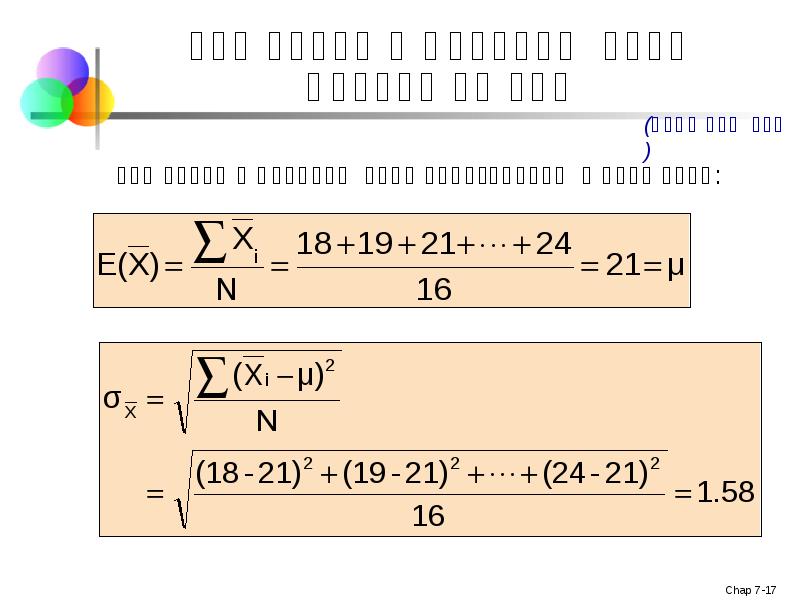
- 17. შერჩევითი განაწილების შემაჯამებელი საზომები:
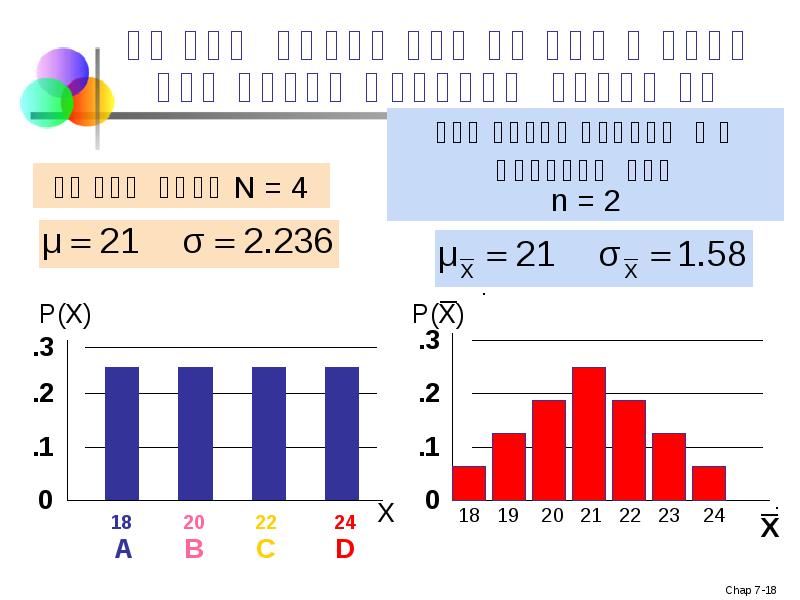
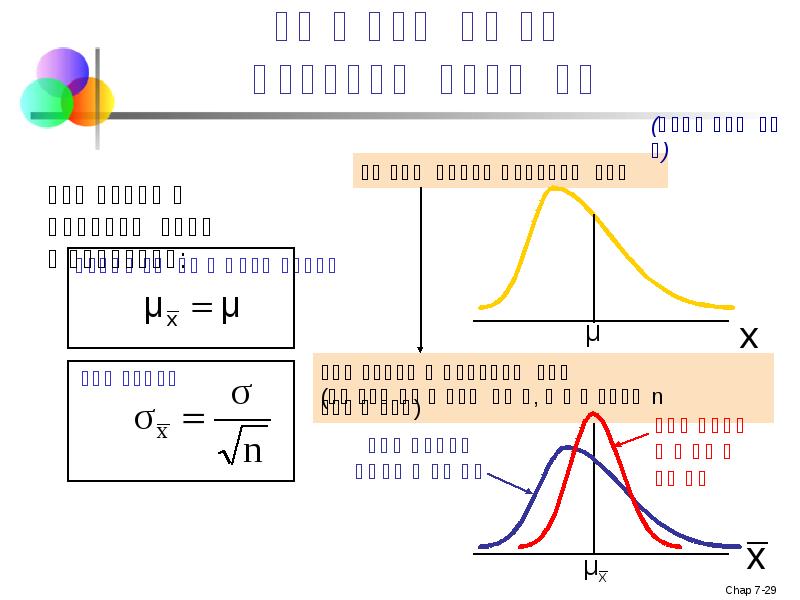
- 18. პოპულაციის შედარება თავის შერჩევის განაწილებასთან
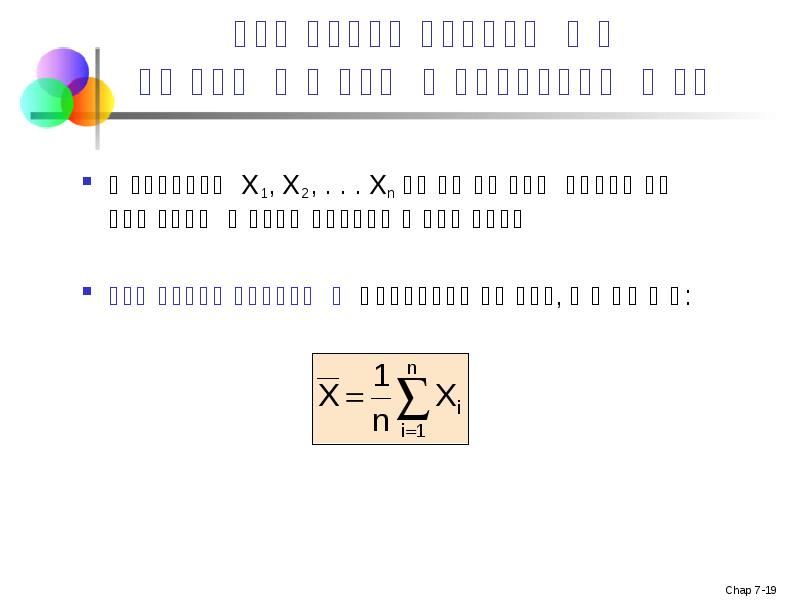
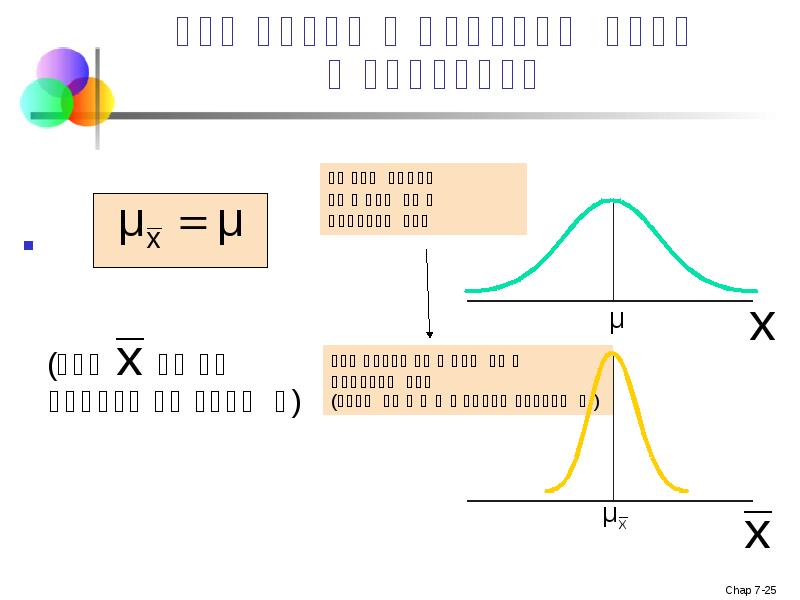
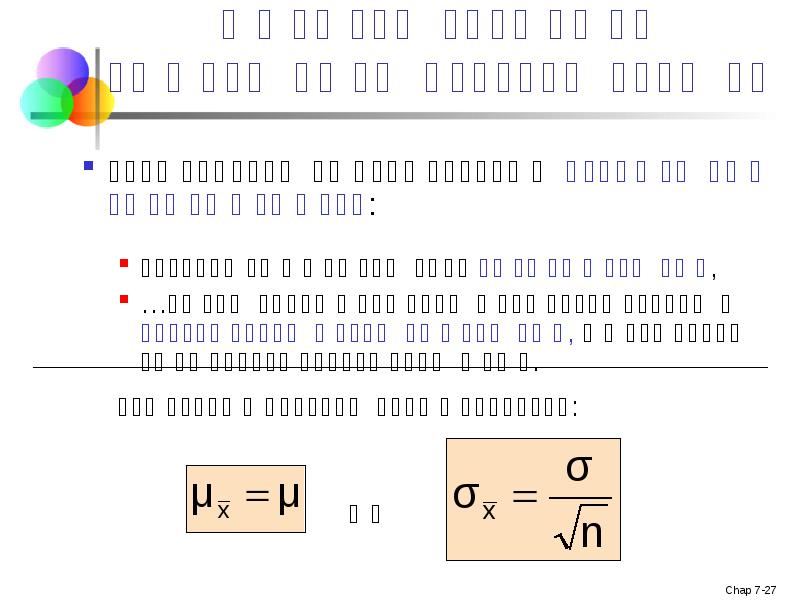
- 19. შერჩევის საშუალოს მოსალოდნელი მნიშვნელობა დავუშვათ X1, X2, . . . Xn
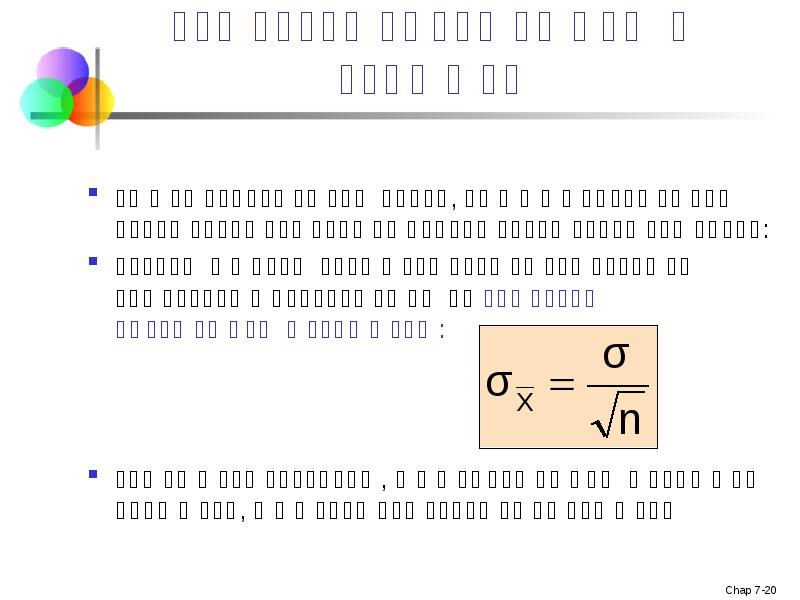
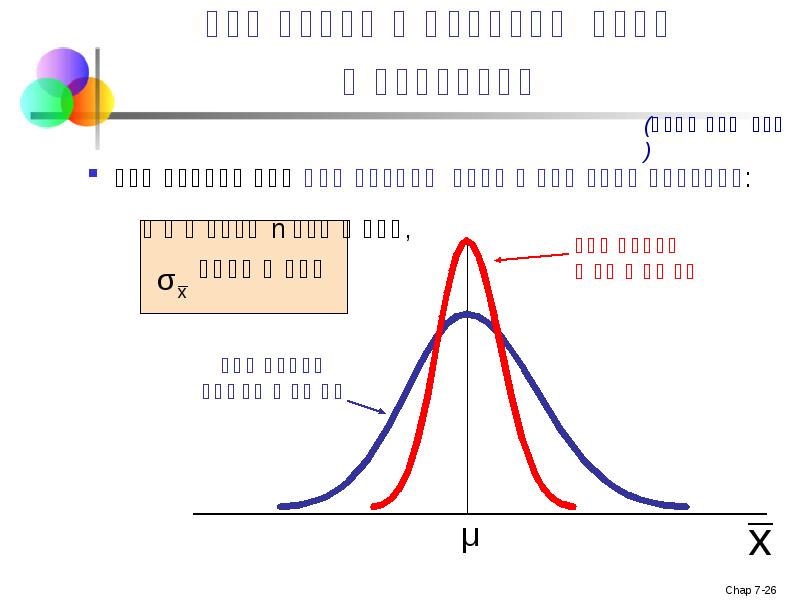
- 20. შერჩევის სტანდარტული შეცდომა ერთიდაიგივე პოპულაციის, ერთი და იგივე ზომის სხვადასხვა შერჩევა
- 21. თუ პოპულაცია ნორმალურია თუ მოპულაცია ნორმალურია საშუალო μ-თი და სტანდარტული გადახრა
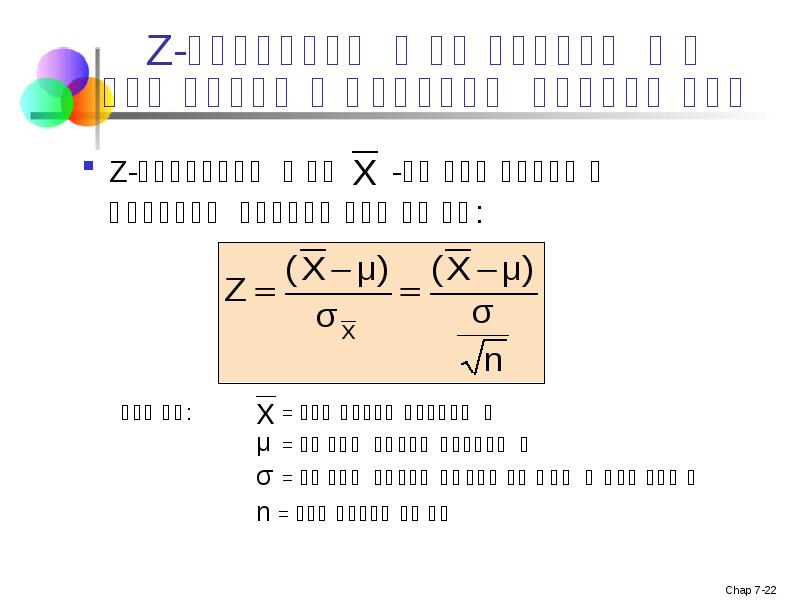
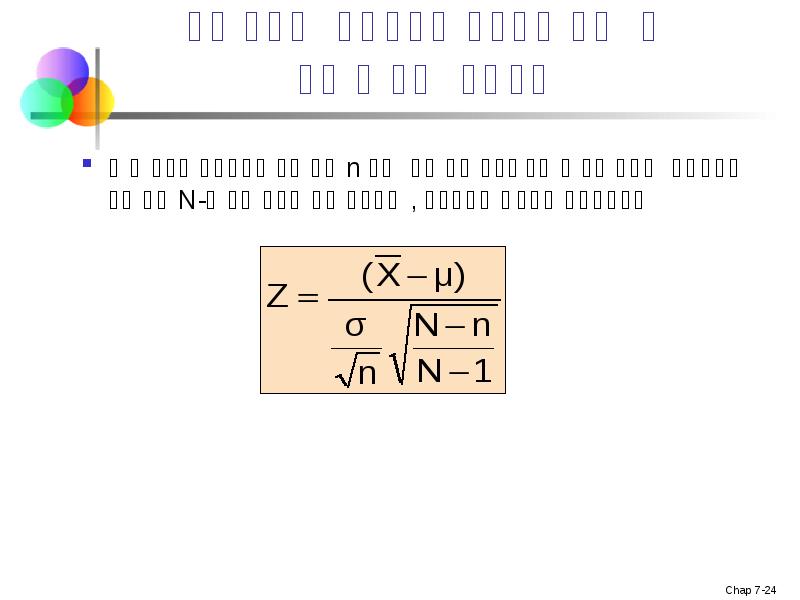
- 22. Z-მნიშვნელობა საშუალოს შერჩევითი განაწილებისათვის Z-მნიშვნელობა -ის შერჩევითი განაწილებისათვის არის:
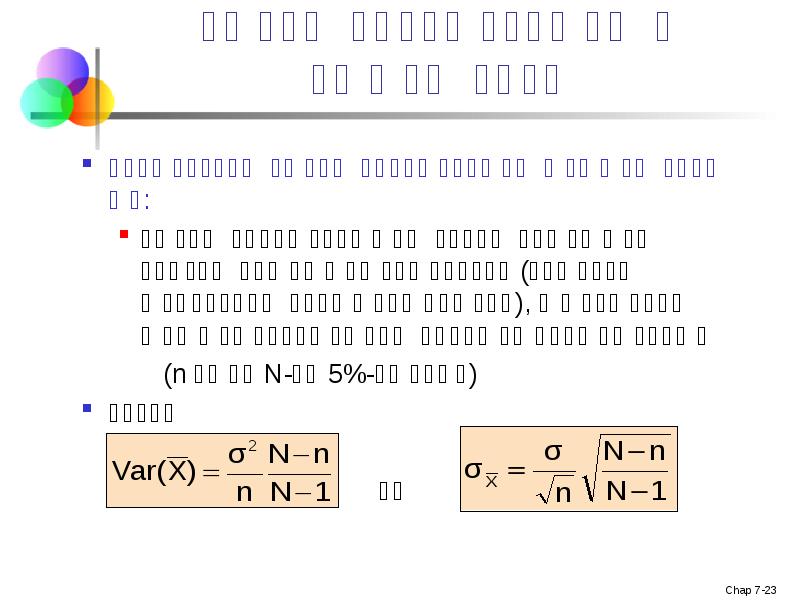
- 23. პოპულაციის სასრული კორელაცია გამოიყენეთ პოპულაციის სასრული კორელაცია თუ: პოპულაციის წევრი არ
- 24. პოპულაციის სასრული კორელაცია თუ შერჩევის ზომა n არ არის პატარა პოპულაციის
- 25. შერჩევითი განაწილების თვისებები (ანუ არის მიუკერძოებელი)
- 26. შერჩევითი განაწილების თვისებები შერჩევისთვის გადანაცვლებადობის შემთხვევაში: როდესაც n იზრდება,
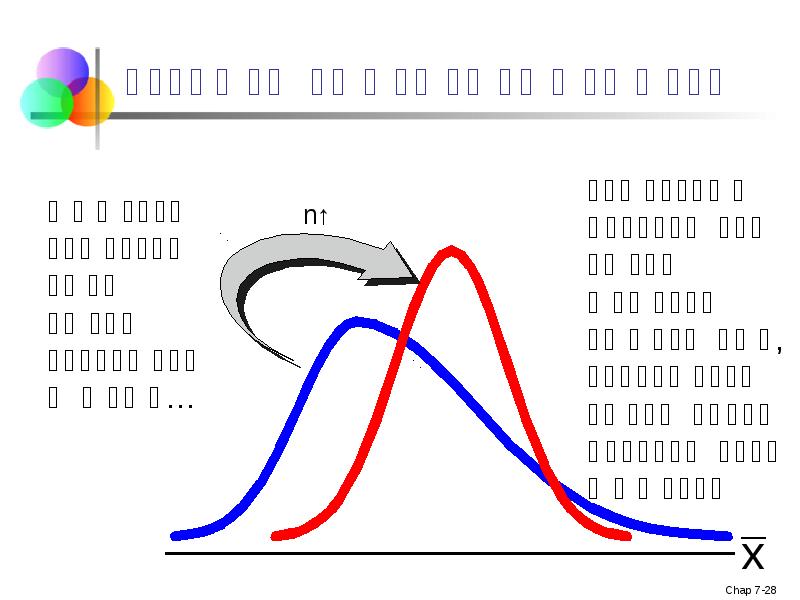
- 27. თუ პოპულაცია არაა ნორმალურად განაწილებულია ჩვენ შეგვიძლია გამოვიყენოთ ცენტრალური ზღვრის თეორემა:
- 28. ცენტრალური ზღვრის თეორემა
- 29. თუ პოპულაცია არაა ნორმალურად განაწილებულია
- 30. რამდენია საკმაოდ დიდი? უმრავლესობა განაწილებისათვის, n > 25 მოგვცემს შეეჩევით განაწილებას,
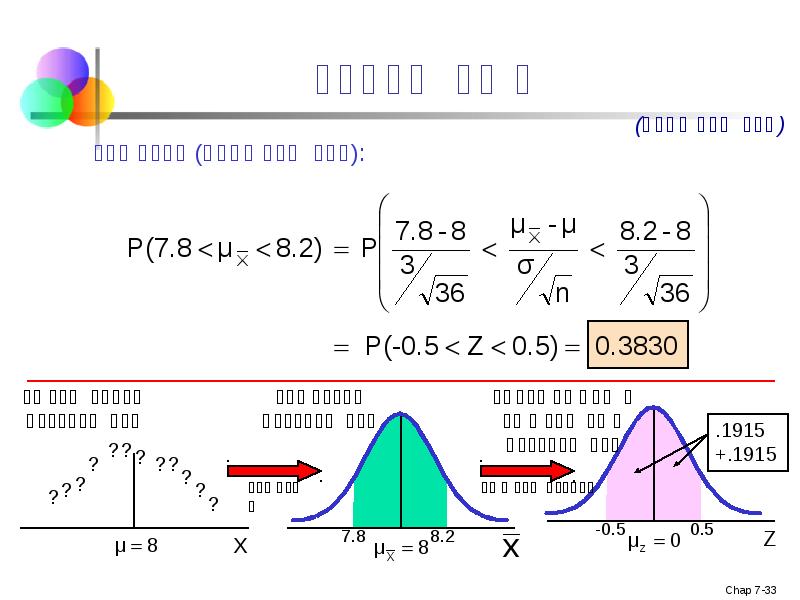
- 31. მაგალითი დავუშვათ პოპულაციის საშუალოა μ = 8 და სტანდარტული გადახრაა σ
- 32. მაგალითი ამოხსნა: მაშინაც კი თუ პოპულაცია ნომრალურად არაა განაწილებული, ცენტრალური ზღვრის
- 33. მაგალითი ამოხსნა (გაგრძელება):
- 34. მისაღები ინტერვალი მიზანი: პოპულაციის საშუალოსა და ვაციაციაზე დაყდრნობით, იმ დიაპაზონის განსაზღვრა,
- 35. Скачать презентацию






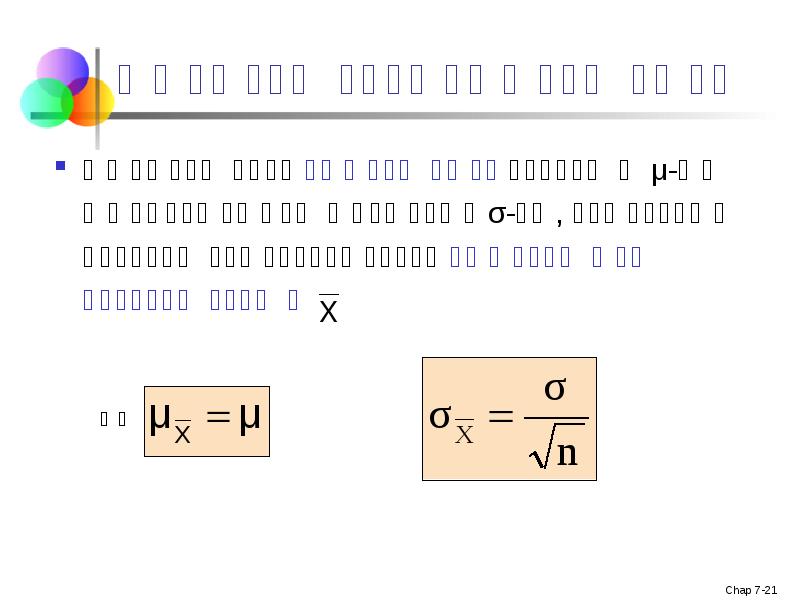




Слайды и текст этой презентации
Скачать презентацию на тему მენეჯერული სტატისტიკა. შერჩევა და შერჩევის განაწილება. თავი 7 можно ниже:
Похожие презентации





























