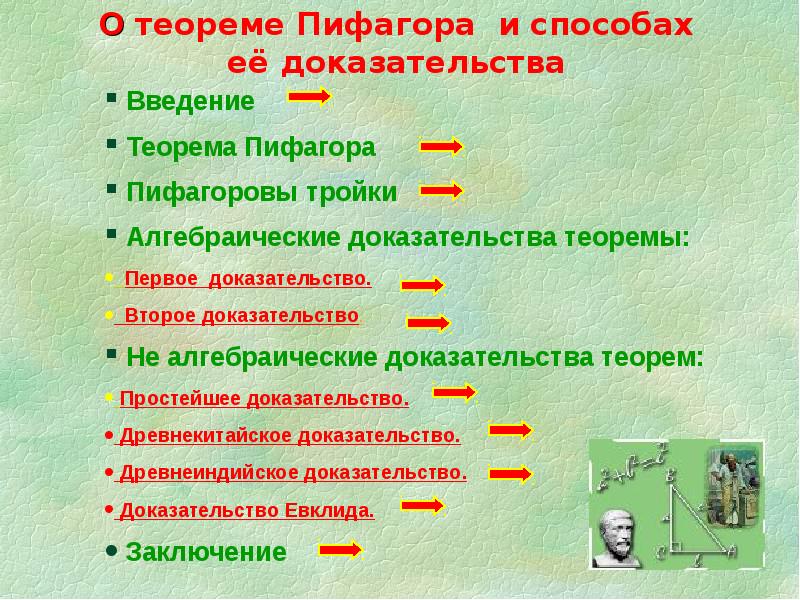
О теореме Пифагора и способах её доказательства

Далеко-далеко. Куда не летают даже самолёты, находится страна Геометрия. Далеко-далеко. Куда не летают даже самолёты, находится страна Геометрия. В этой необычной стране был удивительный город-город Теорем.Однажды в этот город пришла красивая девочка по имени Гипотенуза.Она попробовала снять комнату, но куда бы она не обращалась, ей всюду отказывали.Наконец она подошла к покосившемуся домику и постучала.Ей открыл мужчина, назвавший себя Прямым Углом, и он предложил Гипотенузе поселиться у него.Гипотенуза осталась в доме , в котором жили Прямой Угол и два его маленьких сына по имени Катеты. С тех пор жизнь в доме Прямого Угла пошла по- новому.На окошке Гипотенуза посадила цветы. А в палисаднике развела розы. Дом принял форму прямоугольного треугольника.Обоим Катетам, Гипотенуза очень понравилась и они попросили её остаться навсегда в их доме.По вечерам эта дружная семья собирается за семейным столом.Иногда Прямой Угол играет со своими детишками в прятки.Чаще всего искать приходиться ему, а Гипотенуза прячется так искусно, что найти её бывает очень трудно. Однажды во время игры Прямой угол заметил интересное свойство: если ему удается найти катеты, то отыскать Гипотенузу не составляет труда.Так Прямой Угол пользуется этой закономерностью, надо сказать, очень успешно.На свойстве этого прямоугольного треугольника и основана теорема

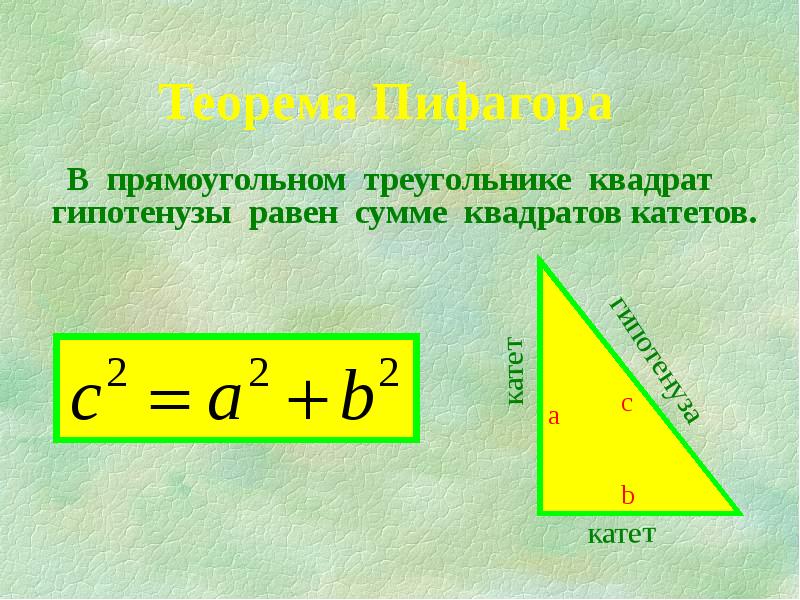
Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Египетский треугольник. Треугольник Пифагора. Прямоугольный треугольник со сторонами 3,4 и 5 имел когда-то большое практическое применение.В частности с помощью его строили прямые углы.Треугольник со сторонами 3, 4 и 5 назвали египетским. Треугольники со сторонами, выраженными целыми числами, называют пифагоровыми. Пр. 5, 12 и 13.Таких треугольников множество, их стороны находят по формулам: m2+n2, m2-n2, 2mn, причем m n.

Пифагоровы числа или пифагоровы тройки. Это великое открытие пифагорейских математиков. Тройки чисел таких, что a2+b2=c2. Интересные особенности этих чисел: Один из «катетов» должен быть кратным трём. Один из «катетов» должен быть кратным четырём. Одно из Пифагоровых чисел должно быть кратно пяти.

Алгебраические доказательства теоремы Предисловие. Еще давно была изобретена головоломка, называемая сегодня “Пифагор”. Нетрудно убедиться в том, что в основе семи частей головоломки лежат равнобедренный прямоугольный треугольник и квадраты, построенные на его катетах, или, иначе, фигуры, составленные из 16 одинаковых равнобедренных прямоугольных треугольников и потому укладывающиеся в квадрат. Такова лишь малая толика богатств, скрытых в жемчужине античной математики — теореме Пифагора. Далее рассмотрим несколько алгебраических доказательств теоремы.

Первое доказательство. (алгебраическое) Пусть Т—прямоугольный треугольник с катетами а, b и гипотенузой с(рис. 6, а). Докажем, что с2=а2+Ь2. Построим квадрат Q со стороной а+Ь (рис. 6, б). На сторонах квадрата Q возьмем точки А, В, С, D так, чтобы отрезки АВ, ВС, CD, DA отсекали от квадрата Q прямоугольные треугольники Т1, Т2, Т3, Т4 с катетами а и b. Четырехугольник ABCD обозначим буквой Р. Покажем, что Р — квадрат со стороной с. Все треугольники Т1, Т2, Т3, Т4 равны треугольнику Т (по двум катетам). Поэтому их гипотенузы равны гипотенузе треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырехугольника прямые. Пусть  и — величины острых углов треугольника Т. Тогда, как вам известно, += 90°. Угол у при вершине А четырехугольника Р вместе с углами, равными  и , составляет развернутый угол. Поэтому +=180°. И так как += 90°, то =90°. Точно так же доказывается, что и остальные углы четырехугольника Р прямые. Следовательно, четырехугольник Р — квадрат со стороной с. Квадрат Q со стороной а+Ь слагается из квадрата Р со стороной с и четырех треугольников, равных треугольнику Т. Поэтому для их площадей выполняется равенство S(Q)=S(P)+4S(T) . Так как S(Q)=(a+b) 2 ; S(P)=c2 и S(T)=1/2(ab), то, подставляя эти выражения в S(Q)=S(P)+4S(T), получаем равенство (a+b) 2=c2+4*(1/2)ab . Поскольку (a+b)2=a2+b2+2ab, то равенство (a+b)2=c2+4*(1/2)ab можно записать так: a2+b2+2ab=c2+2ab. Из равенства a2+b2+2ab=c2+2ab следует, что с2=а2+Ь2. Ч.Т.Д.

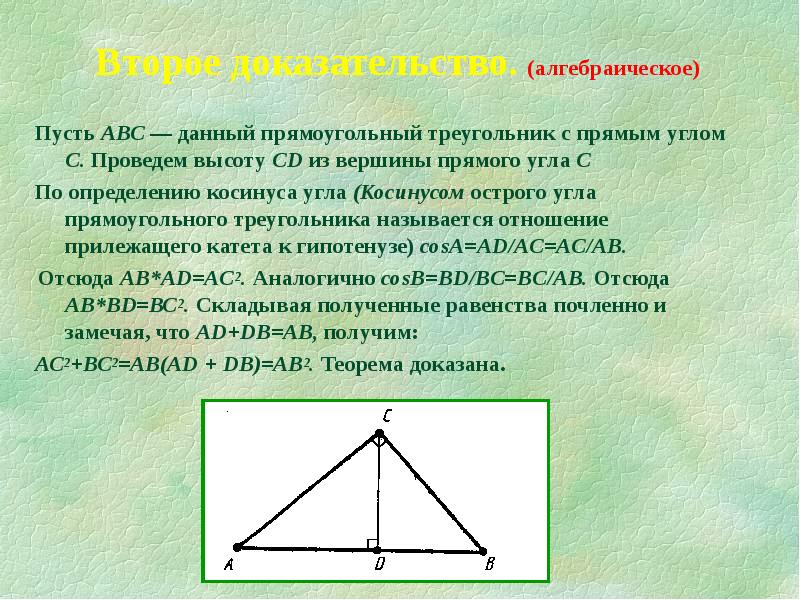
Второе доказательство. (алгебраическое) Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) соsА=AD/AC=AC/AB. Отсюда AB*AD=AC2. Аналогично соsВ=BD/BC=BC/AB. Отсюда AB*BD=ВС2. Складывая полученные равенства почленно и замечая, что AD+DB=AB, получим: АС2+ВС2=АВ(AD + DB)=АВ2. Теорема доказана.

Не алгебраические доказательства теоремы. Простейшее доказательство. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах." Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например, для ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.

Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла тематика в девяти книгах” — главное из сохранившихся математик - астрономических сочинений в книге “Математики” помещен чертеж ,доказывающий теорему Пифагора. Ключ к этому доказательству подобрать нетрудно. Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла тематика в девяти книгах” — главное из сохранившихся математик - астрономических сочинений в книге “Математики” помещен чертеж ,доказывающий теорему Пифагора. Ключ к этому доказательству подобрать нетрудно.

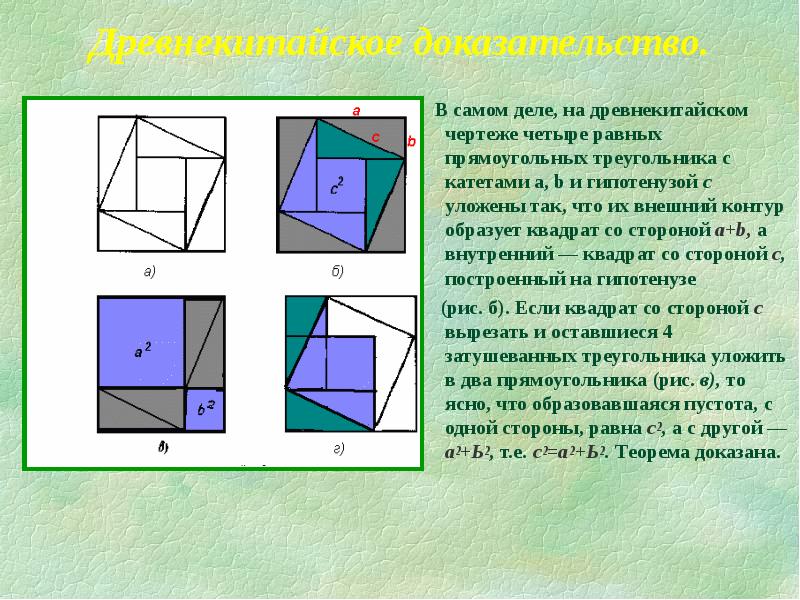
Древнекитайское доказательство. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний — квадрат со стороной с, построенный на гипотенузе (рис. б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана.

Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате “Сиддханта широмани” (“Венец знания”) крупнейшего характерным для индийских доказательств словом “Смотри!”. Как видим, в квадрате индийского математика XII в. Бхаскары помещен чертеж с со стороной а+b изображали четыре прямоугольньных треугольника с катетами длин a и b (рис.1и2).После чего писали одно слово “Смотри!”. И действительно, взглянув на эти рисунки, видим, что слева свободна от треугольников фигура, состоящая из двух квадратов со сторонами a и b,соответственно её площадь равна a²+b², а справа- квадрат со стороной c -его площадь равна c² . Значит, a²+b²=c², что и составляет утверждение теоремы Пифагора.

Доказательство Евклида. Доказательство Евклида приведено в предложении 47 первой книги “Начал”. На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL — квадрату АС КС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе. В самом деле, затушеванные на рисунке треугольники ABD и BFC равны по двум сторонам и углу между ними: FB=AB, BC==BD и FBC=d+ABC=ABD. Но SABD=1/2 SBJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=1\2 SABFH (BF—общее основание, АВ—общая высота). Отсюда, учитывая, что SABD=SFBC , имеем SBJLD= SABFH.Аналогично, используя равенство треугольников ВСК и АСЕ,доказывается, что SJCEL=SACKG. Итак, SABFH+SACKG=SBJLD+SJCEL= SBCED , что и требовалось доказать.

О доказательстве Евклида Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой причине его нередко называли “ходульным” и “надуманным”. Но такое мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном в цепи предложений 1-й книги “Начал”. Для того чтобы логически безупречно построить эту цепь, чтобы каждый шаг доказательства был основан на ранее доказанных предложениях, Евклиду нужен был именно выбранный им путь.

Заключение В заключении еще раз хочется сказать о важности теоремы. Значение ее состоит прежде всего в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. К сожалению, невозможно здесь привести все или даже самые красивые доказательства теоремы, однако хочется надеется, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней.