Пределы. Непрерывность функций

Пределы. Непрерывность функций Автор: Королёв Иван, 11 «А» класс Руководитель: Степанищева Зоя Григорьевна

Введение Цель работы: 1. Совершенствовать уровень своей математической подготовки. 2. Овладеть некоторыми вопросами математического анализа. Задачи исследования: 1. Изучить определения и свойства предела, непрерывность функции. 2. Выработать навыки нахождения пределов, построения графи-ков разрывных функций. Актуальность темы: Изучение данной темы предусматривает межпредметную связь математики и физики. Понятие предела непосредственно связано с ос-новными понятиями математического анализа – производная, инте-грал и др.

Предел переменной величины Пределом переменной величины х называется постоянное число а, если для каждого наперед заданного произвольно малого положи-тельного числа ε можно указать такое значение переменной х, что все последующие значения будут удовлетворять неравенству |х–а|<ε. Если число а есть предел переменной величины х, то пишут: lim x=a. В терминах геометрических определение предела может быть сформулировано следующим образом: постоянное число а есть пре-дел переменной х, если для любой наперед заданной как угодно малой окрестности с центром в точке а и радиусом ε найдется такое значе-ние х, что все точки, соответствующие последующим значениям пере-менной, будут находиться в этой окрестности:

Предел переменной величины Рассмотрим несколько примеров переменных, стремящихся к пределу. Пример 1. Доказать, что переменная хn=1+ имеет предел, равный единице. Составим разность между переменной и ее пределом: |хn–1|=|(1+ )–1|= . Для любого ε все последующие значения перемен-ной, начиная с номера n, где n > , будут удовлетворять условию |хn–1|<ε, что и требовалось доказать. Пример 2. Доказать, что переменная wn=(-1)n при неогра-ниченном возрастании n не имеет предела. Действительно, при возрастании n, переменная wn не стремится ни к какому числу, попеременно принимая значения 1 и –1, т. е. не имеет предела.

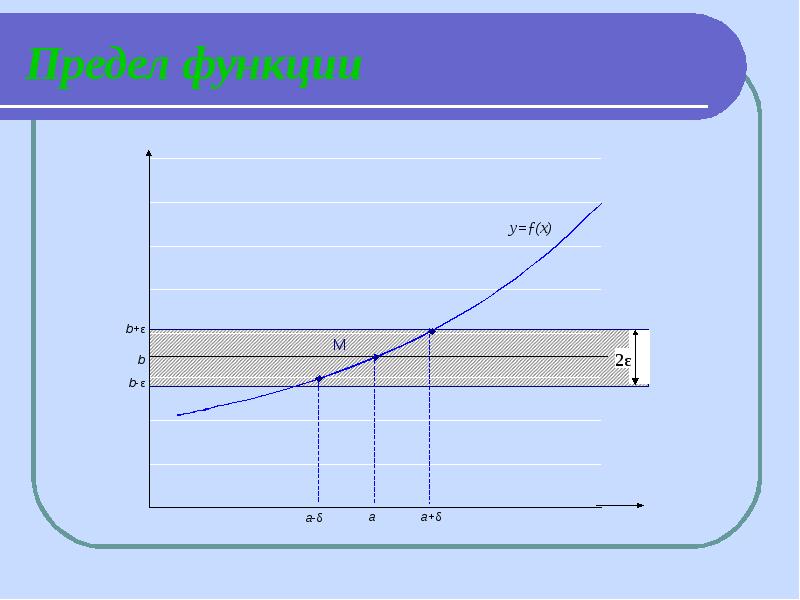
Предел функции Пределом функции ƒ(х) при х→а называется число b, если для любого положительного ε можно указать такое положительное число δ, что для любого х, удовлетворяющего неравенству |х–а|<δ, выполняется неравенство|f(x)–b|<ε. В этом случае пишут: ƒ(х)= b. Если х→а и х<а, то употребляют запись ƒ(х)=b1; если же х→а, но х>а, то пишут ƒ(х)=b2. Числа b1 и b2 называются соот-ветственно левым и правым пределом функции у=ƒ(х).

Предел функции

Основные свойства пределов Свойство 1. Предел суммы нескольких переменных равен сумме пределов этих переменных: lim(a1+a2+…+an)= lim a1+lim a2+…+lim an. Свойство 2. Предел произведения нескольких переменных равен произведению пределов этих переменных: lim(a1∙a2∙…∙an)= lim a1∙lim a2∙…∙lim an. Свойство 3. Предел частного двух переменных равен част-ному пределов этих переменных, если предел знаменателя отли-чен от нуля: lim = , если lim b≠0. Свойство 4. Предел степени равен пределу основания, воз-веденного в степень предела показателя: lim ab=(lim a)lim b.

Основные свойства пределов Первый замечательный предел: Второй замечательный предел: Далее я решил привести некоторые часто встречающиеся типы примеров, рассмотренных мной в ходе работы: 1. 2.

Основные свойства пределов 3. 4.

Основные свойства пределов 5. 6. Пусть и=2+а, а→0.

Непрерывность функций Функция называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и существует предел функции при х→х0, равный значению самой функции в этой точке. Функция на-зывается непрерывной в некоторой области, если она непрерывна в каждой точке этой области. Точка х0, принадлежащая области опреде-ления функции, называется точкой разрыва, если в этой точки нару-шается условие непрерывности. Если существуют конечные левый и правый пределы функции в точке х0, а функции определена в этой точке, но эти три числа не равны между собой, то точка х0 называется точкой разрыва I рода. Точки разрыва, не являющиеся точками разры-ва I рода, называются точками разрыва II рода.

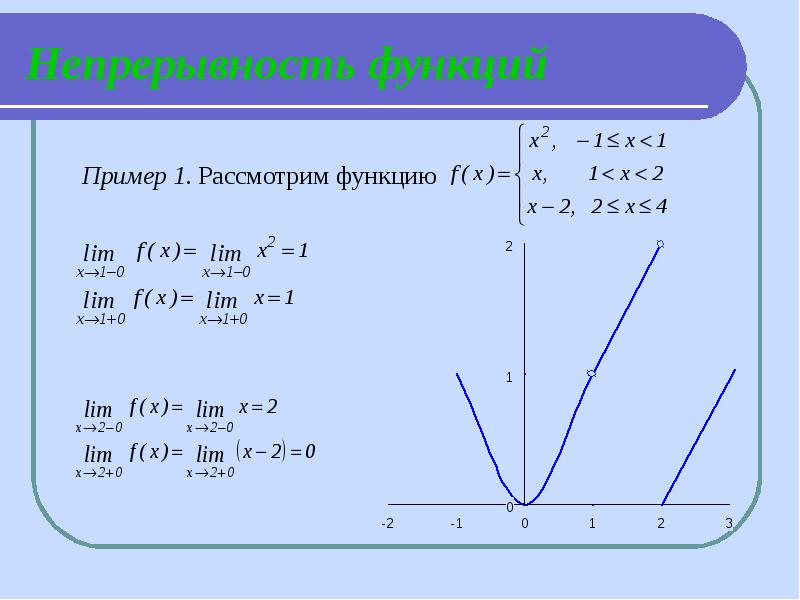
Непрерывность функций Пример 1. Рассмотрим функцию

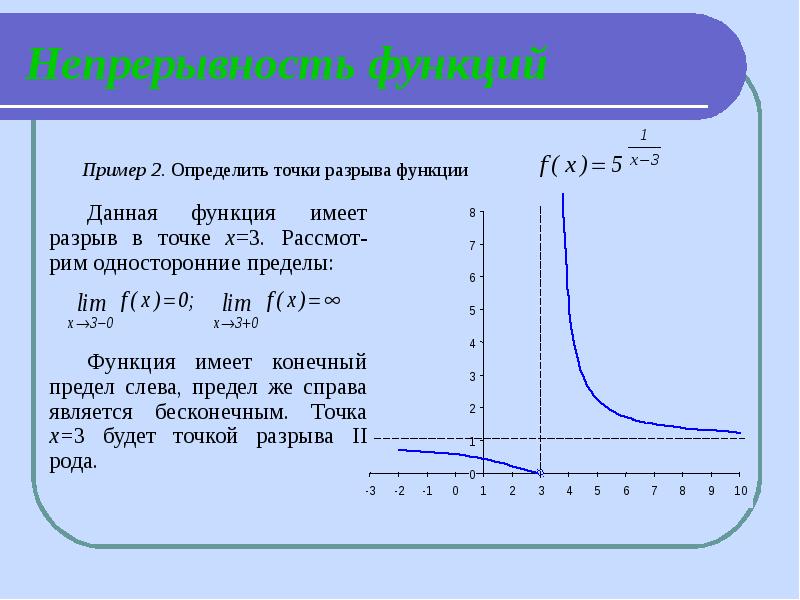
Непрерывность функций Данная функция имеет разрыв в точке х=3. Рассмот-рим односторонние пределы: Функция имеет конечный предел слева, предел же справа является бесконечным. Точка х=3 будет точкой разрыва II рода.