Презентация по геометрии на темы "Касательная к окружности" и "Вписанные, центральные углы." презентация
Содержание
- 2. Если расстояние от центра окружности до прямой равно радиусу , то
- 3. Касательная к окружности Прямая, имеющая с окружностью только одну общую точку,
- 4. Касательная к окружности. Теорема: касательная окружности перпендикулярна к радиусу,проведенному в точку
- 5. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют
- 6. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна
- 7. Угол с вершиной в центре окружности называется ее центральным углом .
- 8. Если АОВ (центральный) неразвернутый, то говорят, что АВ, расположенная
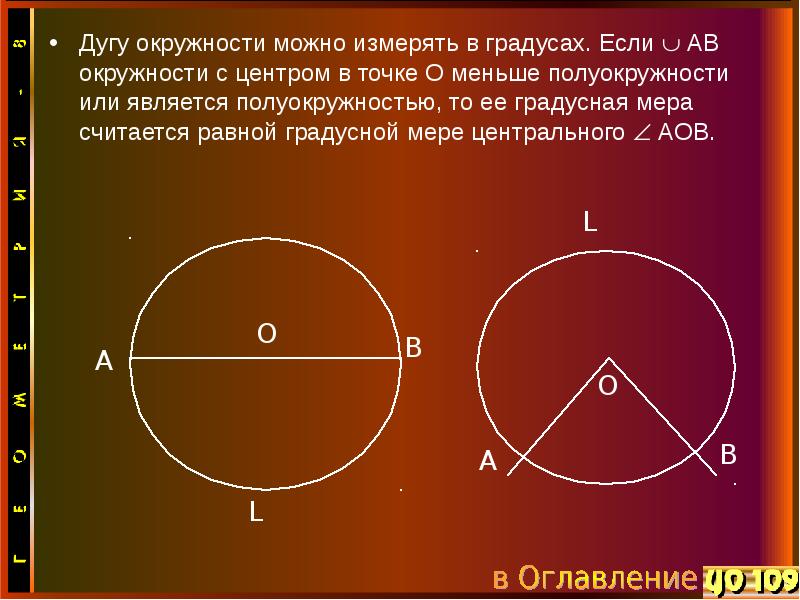
- 9. Дугу окружности можно измерять в градусах. Если АВ окружности с
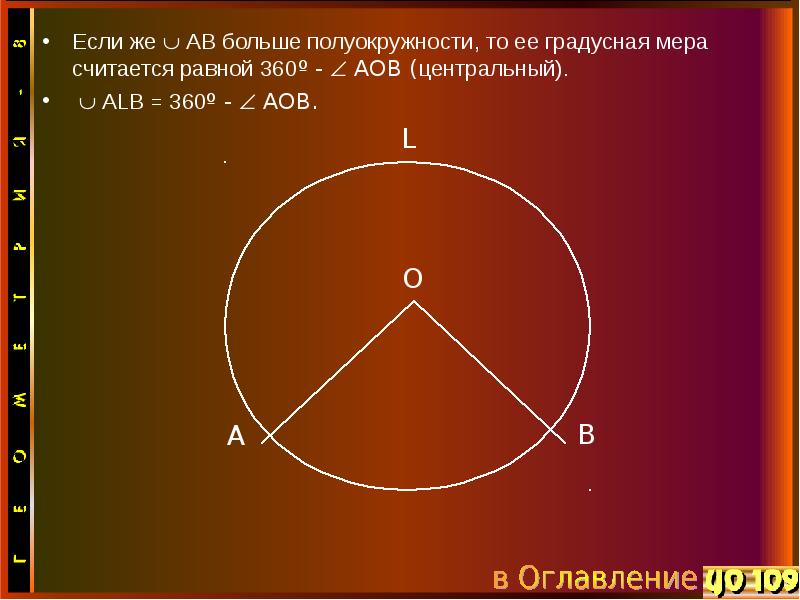
- 10. Если же АВ больше полуокружности, то ее градусная мера считается
- 11. Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется
- 12. Вписанный угол измеряется половиной дуги на которую он опирается Пусть
- 13. Рассмотрим 1 случай расположения луча ВО относительно АВС. Например луч
- 14. Рассмотрим 2 случай, когда луч ВО делит АВС на два
- 15. Рассмотрим 3 случай расположения луча ВО относительно АВС АВD
- 16. РАССМОТРИМ 1 СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ Вписанные углы , опирающиеся на одну
- 17. Рассмотрим 2 следствие из теоремы Вписанный угол, опирающийся на полуокружность
- 18. Скачать презентацию















Слайды и текст этой презентации
Скачать презентацию на тему Презентация по геометрии на темы "Касательная к окружности" и "Вписанные, центральные углы." можно ниже:
Похожие презентации





























