Propositional logic презентация
Содержание
- 2. Propositions Our discussion begins with an introduction to the basic building
- 3. Propositions Example 1 All the following declarative sentences are propositions.
- 4. Propositions Example 2 Consider the following sentences. 1. What time is
- 5. Propositions We use letters to denote propositional variables (or statement variables),
- 6. Propositions The area of logic that deals with propositions is called
- 7. Compound propositions We now turn our attention to methods for producing
- 8. Compound propositions Many mathematical statements are constructed by combining one or
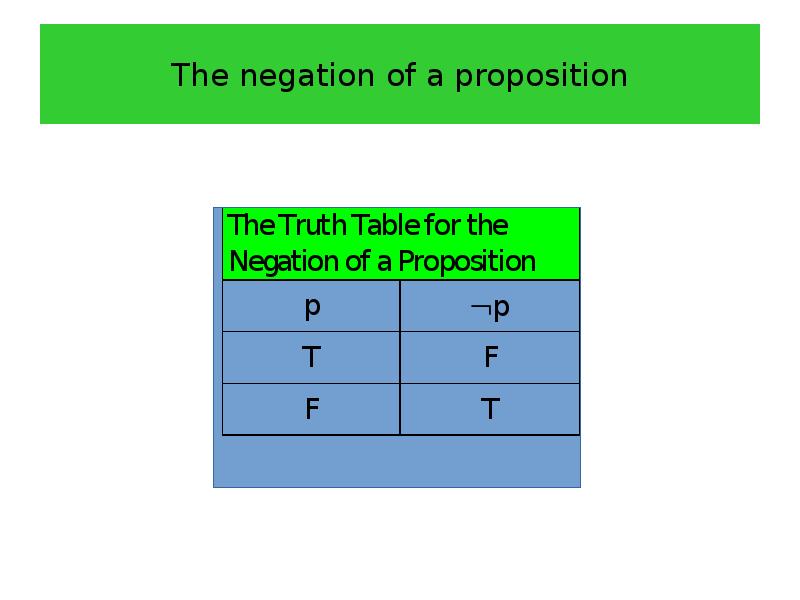
- 9. The negation of a proposition Definition 2 Let p be
- 10. The negation of a proposition
- 11. The negation of a proposition Example 3 Find the negation of
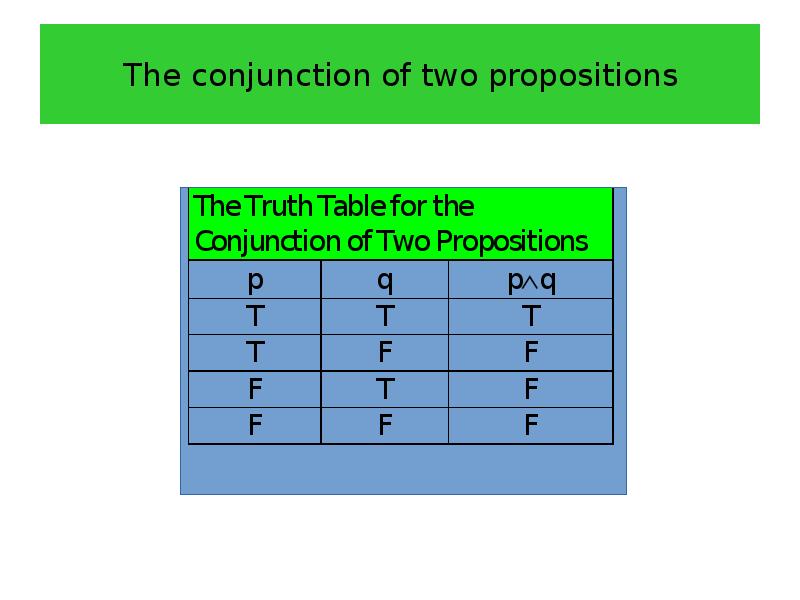
- 12. The conjunction of two propositions Definition 3 Let p and
- 13. The conjunction of two propositions
- 14. The conjunction of two propositions Example 4 Find the conjunction of
- 15. The conjunction of two propositions Solution The conjunction
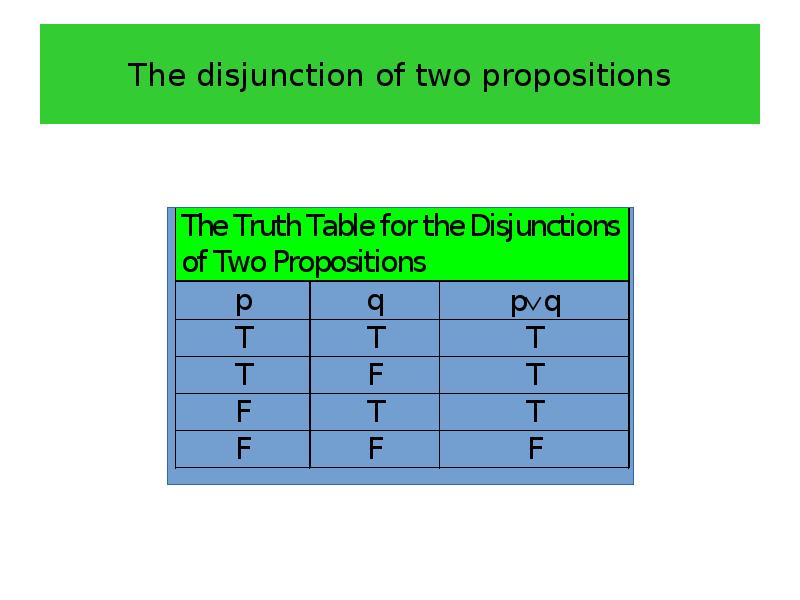
- 16. The disjunction of two propositions Definition 4 Let p and
- 17. The disjunction of two propositions
- 18. The disjunction of two propositions Example 5 Find the disjunction of
- 19. The disjunction of two propositions Solution The disjunction
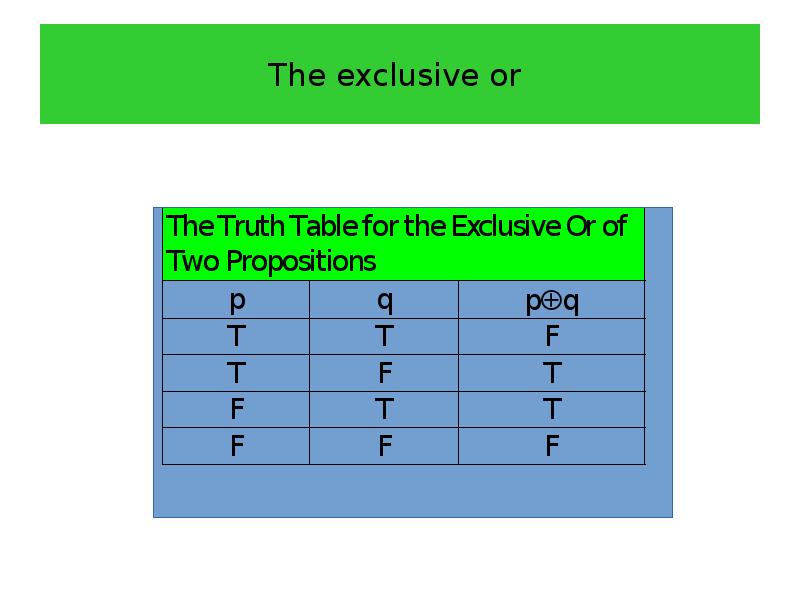
- 20. The exclusive or The use of the connective or in
- 21. The exclusive or On the other hand, we are using
- 22. The exclusive or Definition 5 Let p and q
- 23. The exclusive or
- 24. Conditional statements Definition 6 Let and be propositions. The conditional
- 25. Conditional statements
- 26. Conditional statements The statement is called a conditional statement because asserts
- 27. Conditional statements Because conditional statements play such an essential role in
- 28. Conditional statements Example 6 Let be the statement “Maria learns discrete
- 29. Converse, contrapositive and inverse We can form some new conditional
- 30. Converse, contrapositive and inverse Example 7 What are the contrapositive,
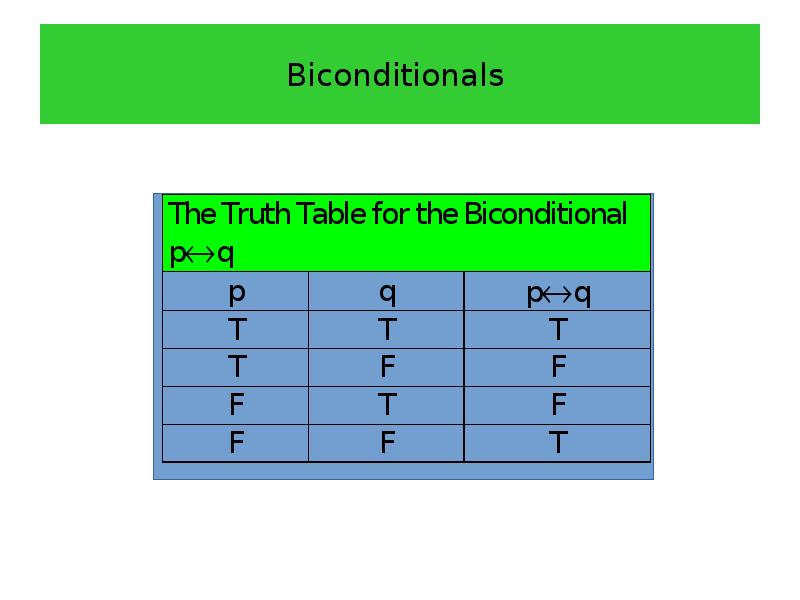
- 31. Biconditionals We now introduce another way to combine propositions that
- 32. Biconditionals
- 33. Biconditionals Note that the statement pq is true when both
- 34. Biconditionals Example 8 Let be the statement “You can
- 35. Truth tables of compound propositions We have now introduced four important
- 36. Truth tables of compound propositions We can use truth tables to
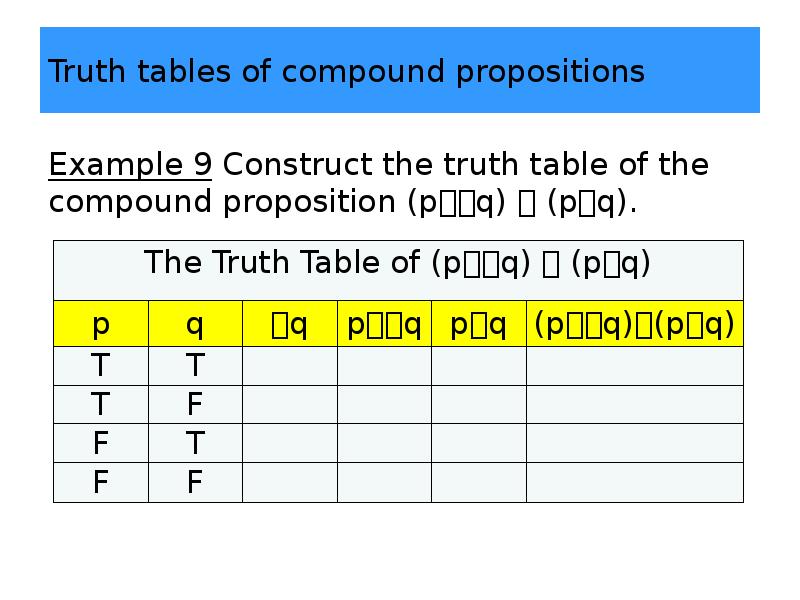
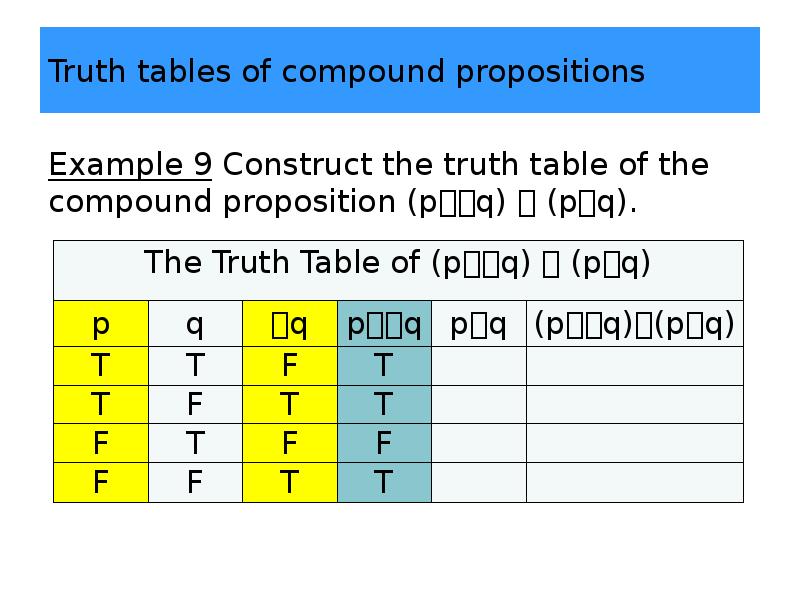
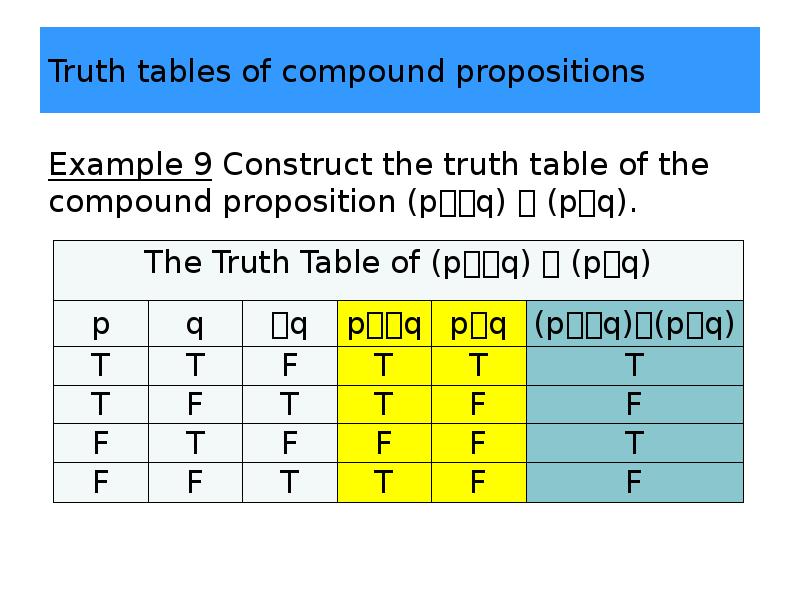
- 37. Truth tables of compound propositions Example 9 Construct the truth table
- 38. Truth tables of compound propositions Example 9 Construct the truth table
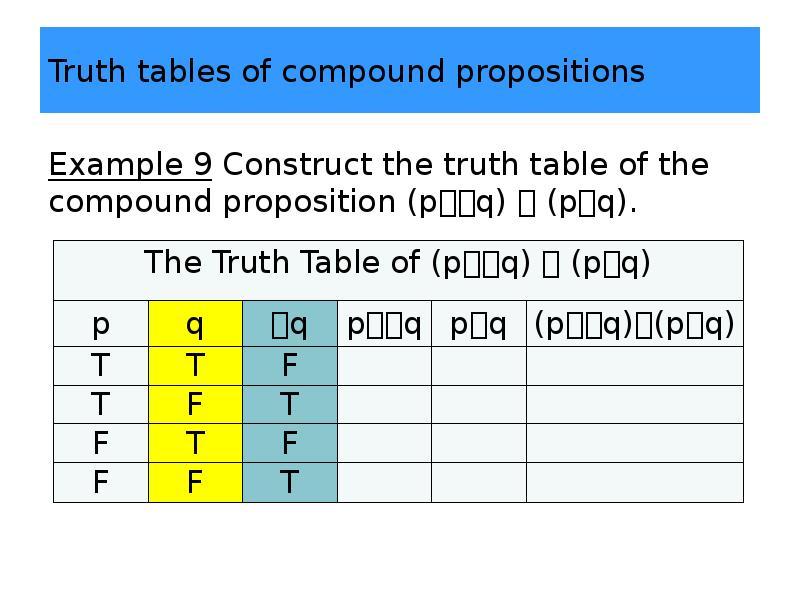
- 39. Truth tables of compound propositions Example 9 Construct the truth table
- 40. Truth tables of compound propositions Example 9 Construct the truth table
- 41. Truth tables of compound propositions Example 9 Construct the truth table
- 42. Truth tables of compound propositions Example 9 Construct the truth table
- 43. Truth tables of compound propositions Example 9 Construct the truth table
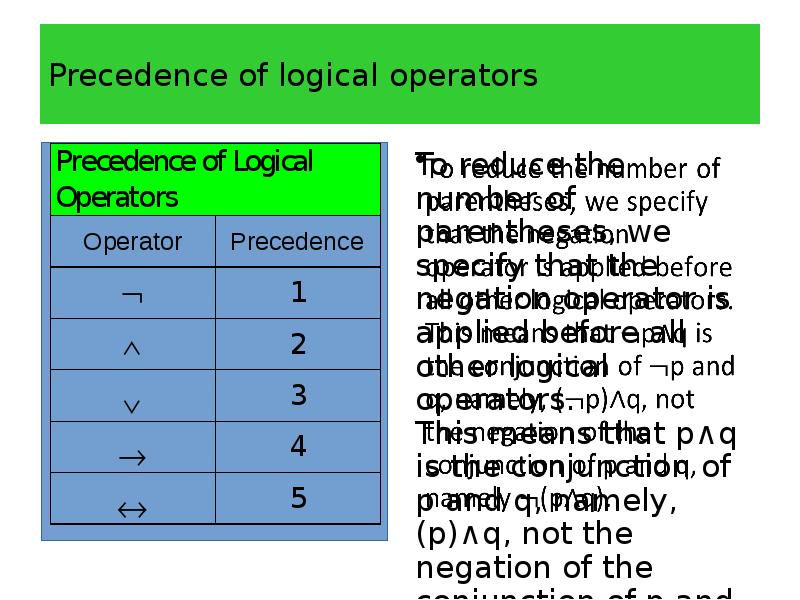
- 44. Precedence of logical operators We can construct compound propositions using the
- 45. Precedence of logical operators This table displays the precedence levels of
- 46. Precedence of logical operators To reduce the number of parentheses, we
- 47. Precedence of logical operators Another general rule of precedence is that
- 48. Precedence of logical operators Finally, it is an accepted rule that
- 49. Tautologies and contradictions Definition 8 A compound proposition that is always
- 50. Tautologies and contradictions Example 10 We can construct examples of tautologies
- 51. Tautologies and contradictions Example 10 Because p∨p is always true, it
- 52. Logical equivalences Definition 9 The compound propositions p and q
- 53. Logical equivalences One way to determine whether two compound propositions are
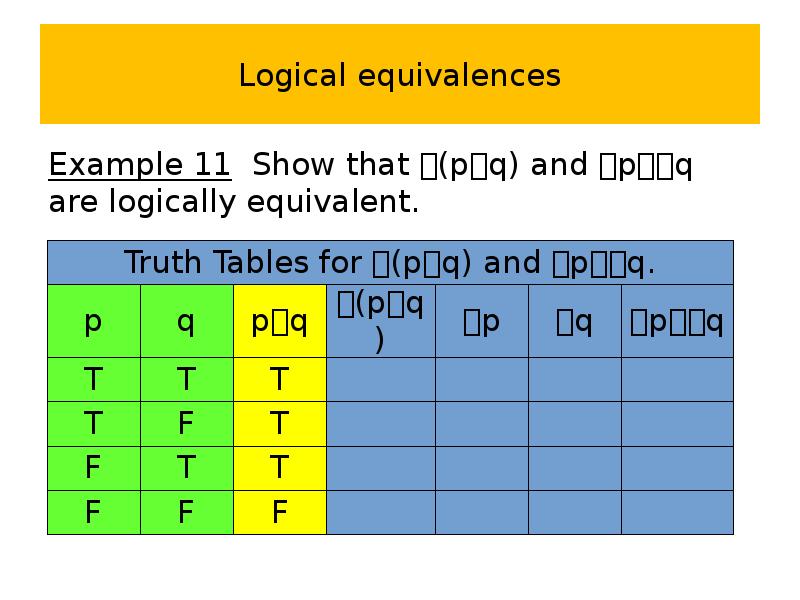
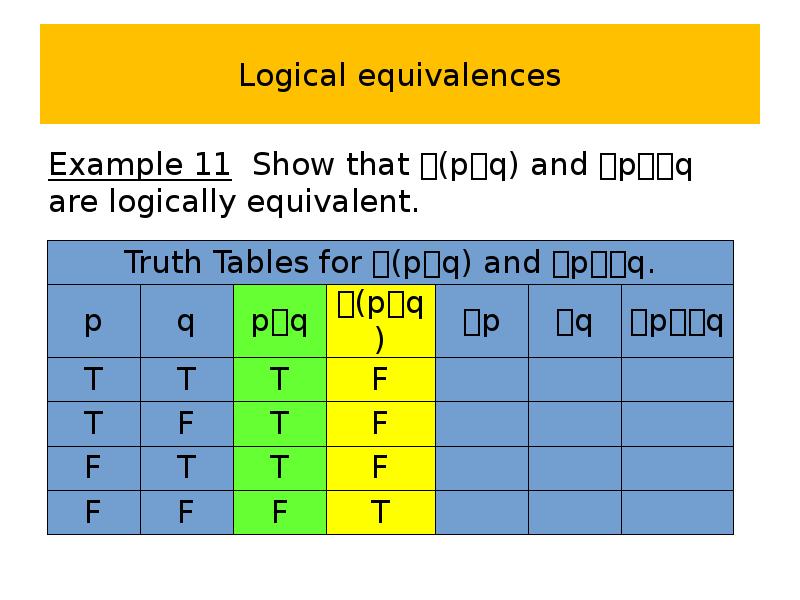
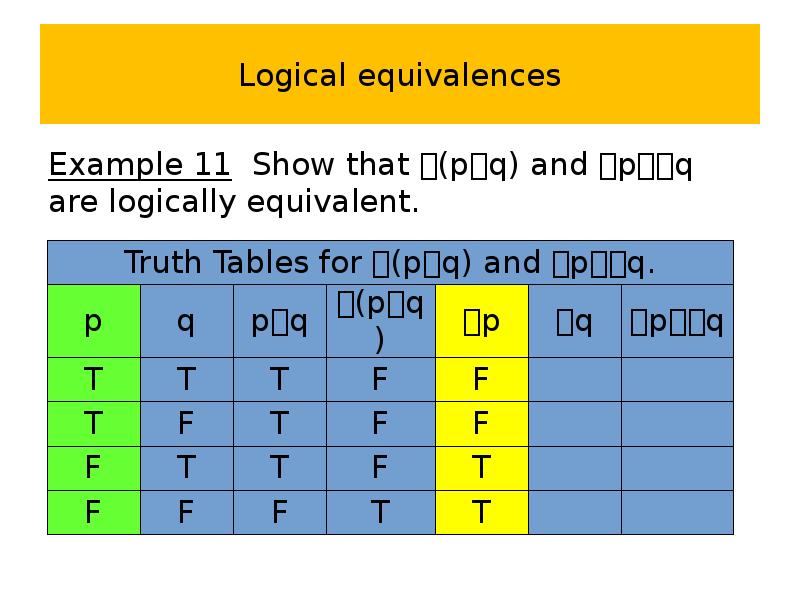
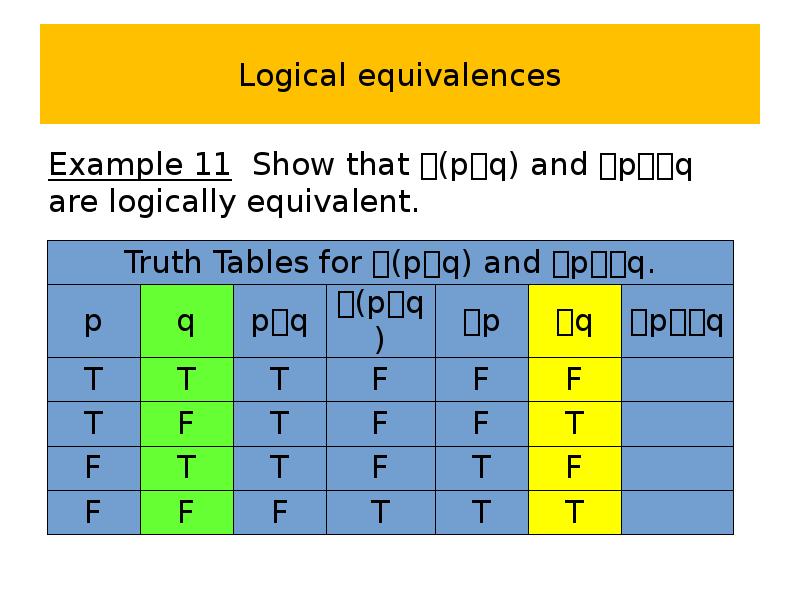
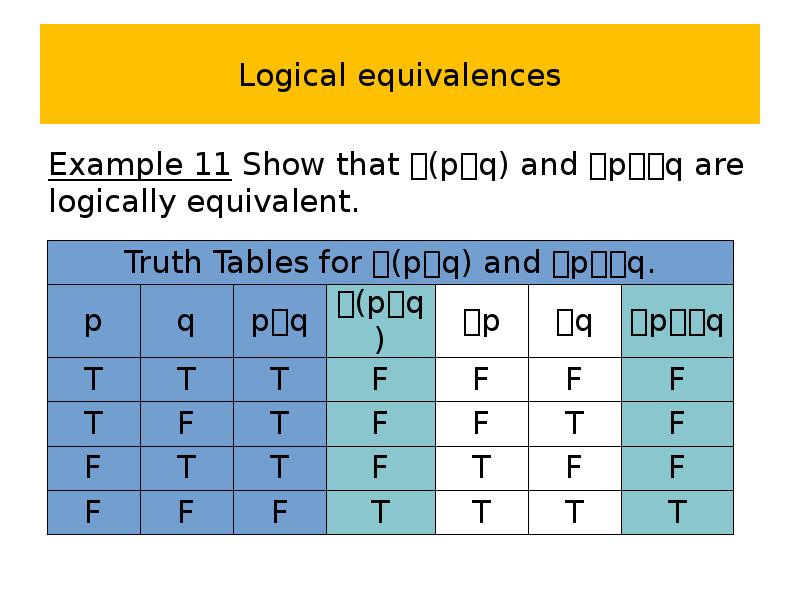
- 54. Logical equivalences Example 11 Show that (pq) and pq are logically
- 55. Logical equivalences Example 11 Show that (pq) and pq are logically
- 56. Logical equivalences Example 11 Show that (pq) and pq are logically
- 57. Logical equivalences Example 11 Show that (pq) and pq are logically
- 58. Logical equivalences Example 11 Show that (pq) and pq are logically
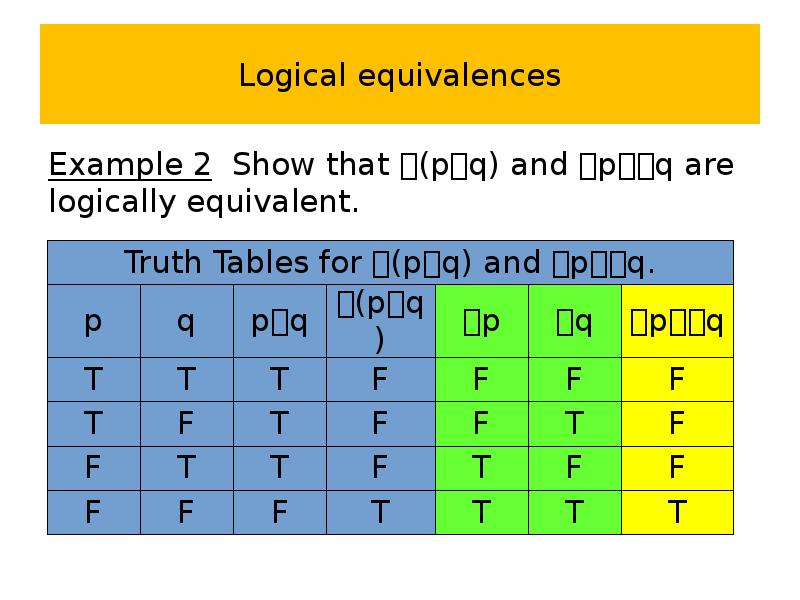
- 59. Logical equivalences Example 2 Show that (pq) and pq are logically
- 60. Logical equivalences Example 11 Show that (pq) and pq are logically
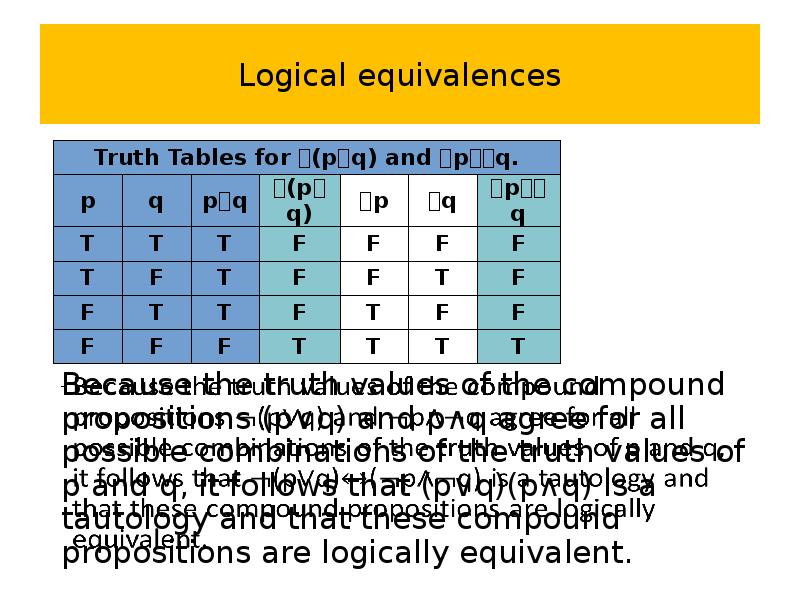
- 61. Logical equivalences
- 62. Logical equivalences (pq) pq This logical equivalence is
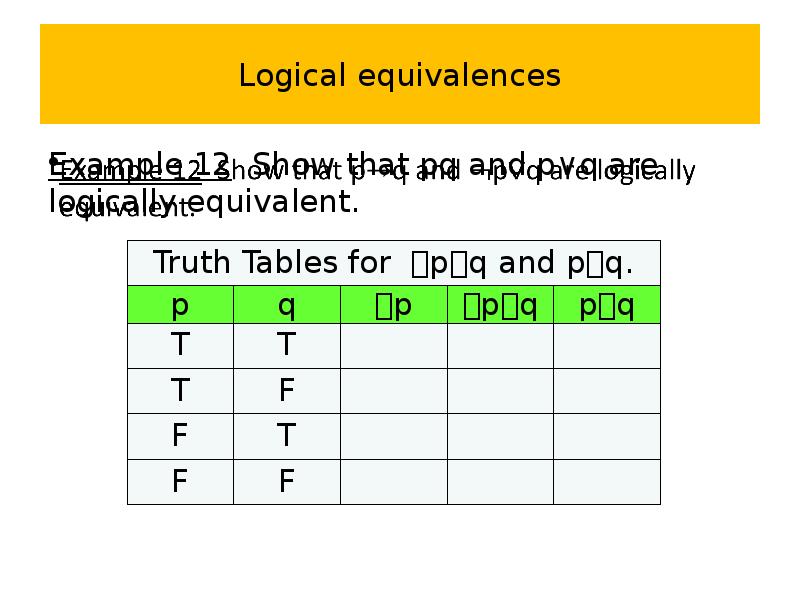
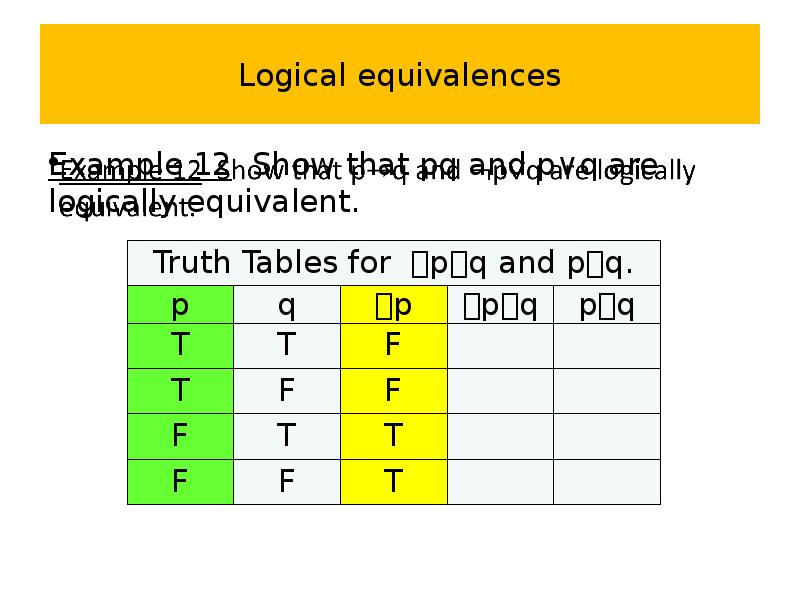
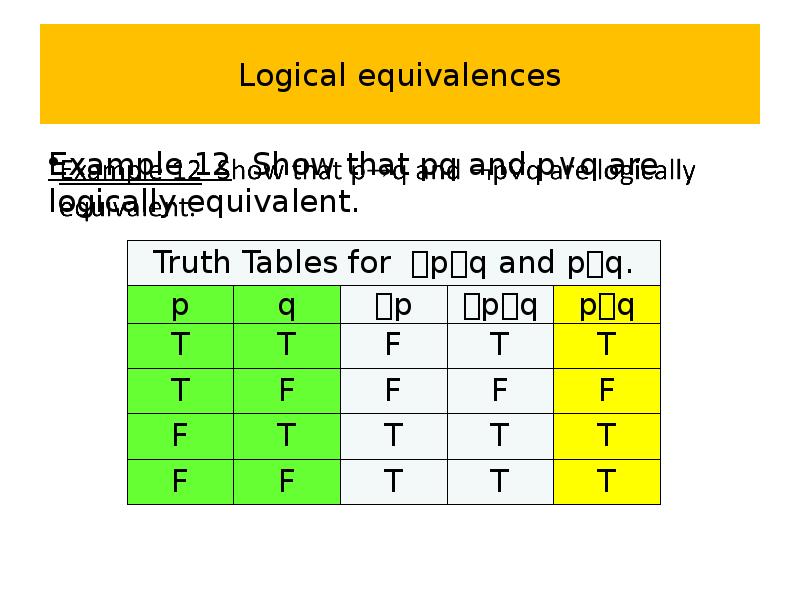
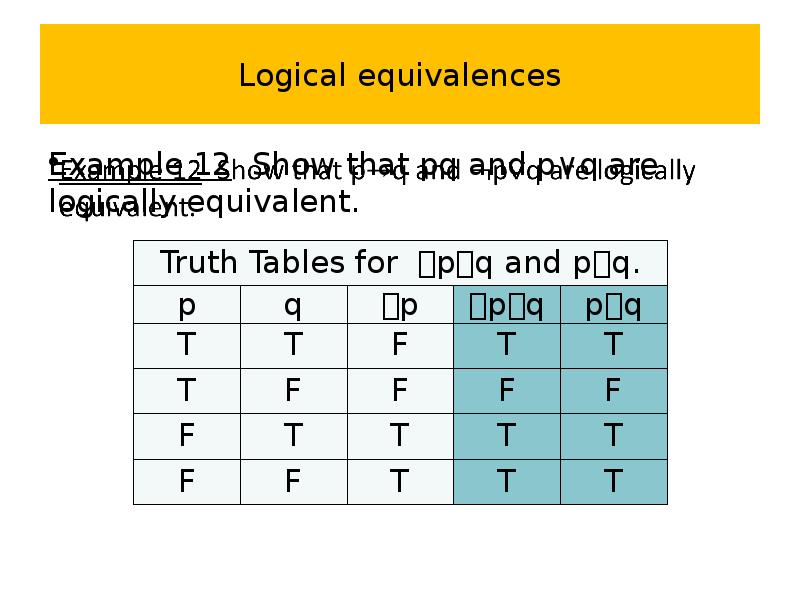
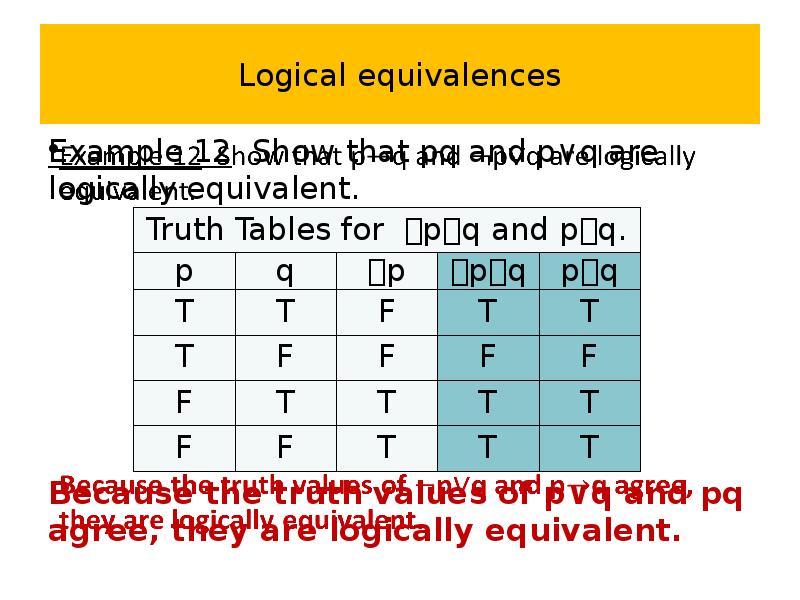
- 63. Logical equivalences Example 12 Show that pq and p∨q are logically
- 64. Logical equivalences Example 12 Show that pq and p∨q are logically
- 65. Logical equivalences Example 12 Show that pq and p∨q are logically
- 66. Logical equivalences Example 12 Show that pq and p∨q are logically
- 67. Logical equivalences Example 12 Show that pq and p∨q are logically
- 68. Logical equivalences Example 12 Show that pq and p∨q are logically
- 69. Logical equivalences Example 12 Show that pq and p∨q are logically
- 70. Logical equivalences We will now establish a logical equivalence of two
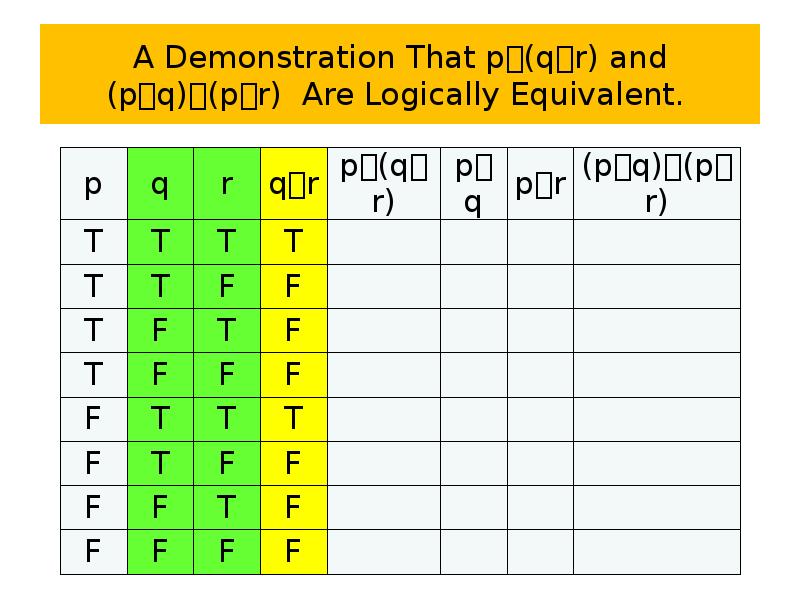
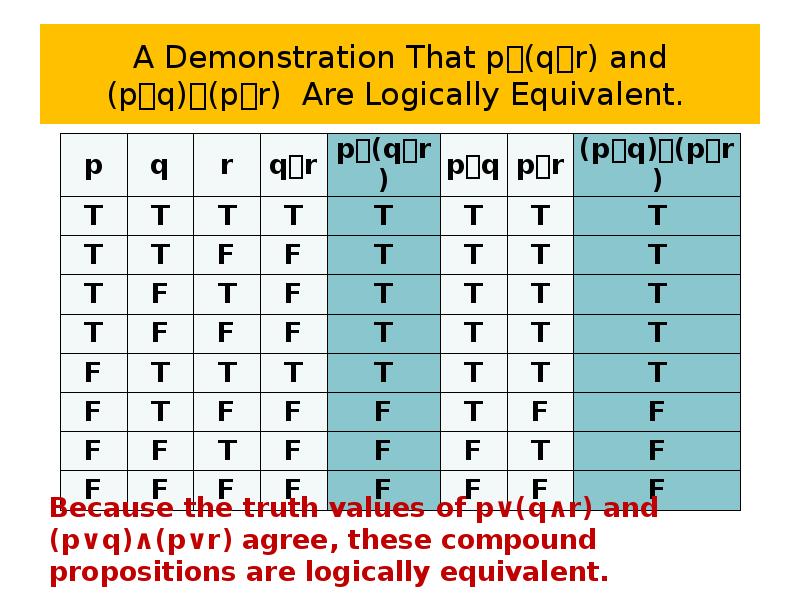
- 71. Logical equivalences Example 13 Show that p∨(q∧r) and (p∨q)∧(p∨r) are logically
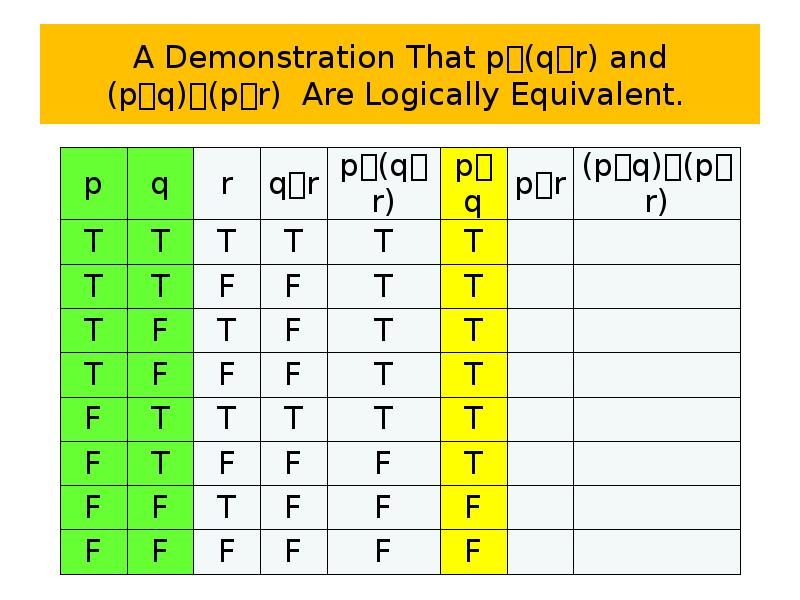
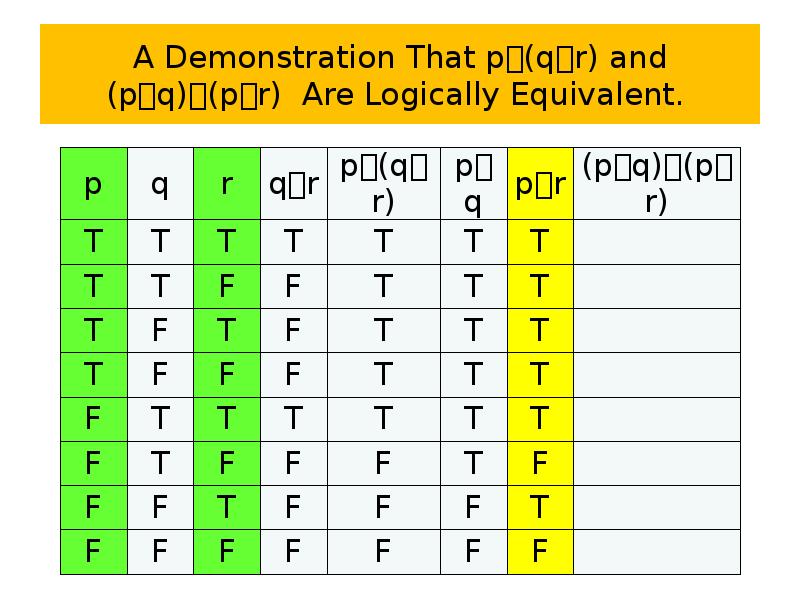
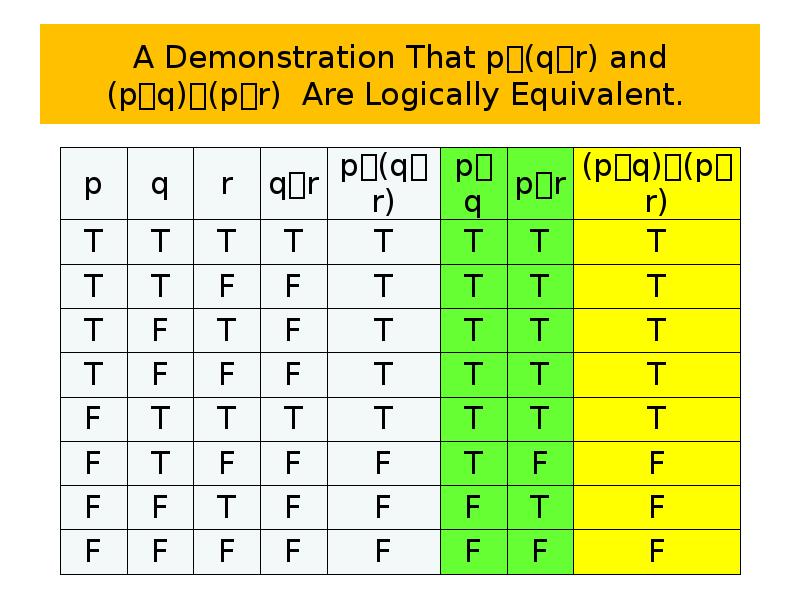
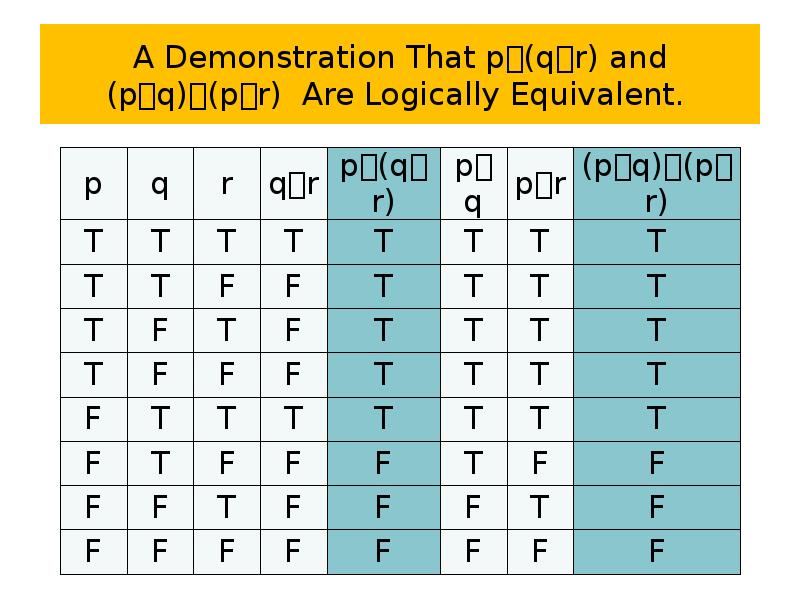
- 72. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 73. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 74. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 75. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 76. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 77. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 78. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 79. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
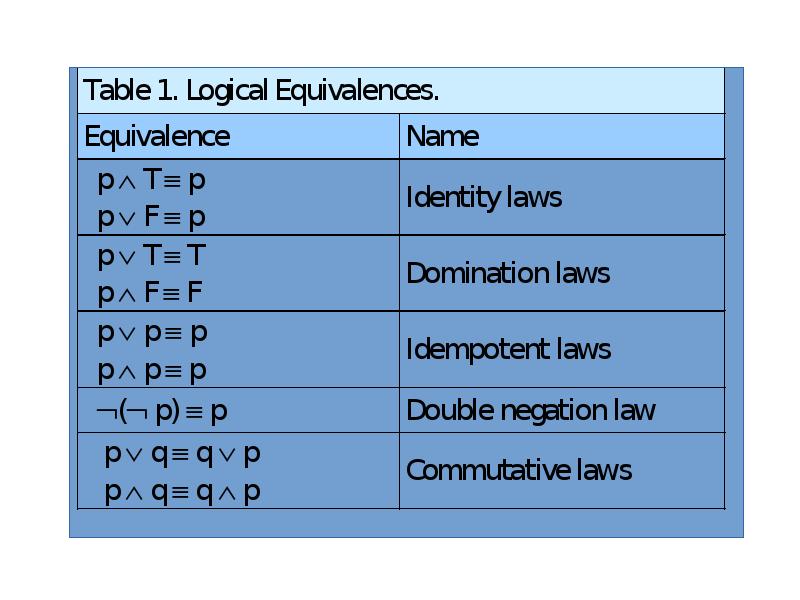
- 80. Logical equivalences Next table contains some important equivalences. In these
- 83. Logical equivalences Boolean algebra of propositions is a set P of
- 84. Logical equivalences We also display some useful equivalences for compound propositions
- 87. Using De Morgan’s Laws Example 13 Use De Morgan’s laws to
- 88. Using De Morgan’s Laws Example 13 Use De Morgan’s laws to
- 89. Constructing new logical equivalences The logical equivalences in Table 1, as
- 90. Constructing new logical equivalences This technique is illustrated in Examples 14
- 91. Constructing new logical equivalences Example 14 Show that (p q)
- 92. Constructing new logical equivalences Example 14 Show that (p q)
- 93. Constructing new logical equivalences Example 15 Show that (p (p
- 94. Constructing new logical equivalences Example 15 Show that (p (p
- 95. Constructing new logical equivalences Example 16 Show that (p q)
- 96. Propositional satisfiability Definition 10 A compound proposition is satisfiable if there
- 97. Propositional satisfiability Definition 11 When we find a particular assignment
- 98. Propositional satisfiability However, to show that a compound proposition is unsatisfiable,
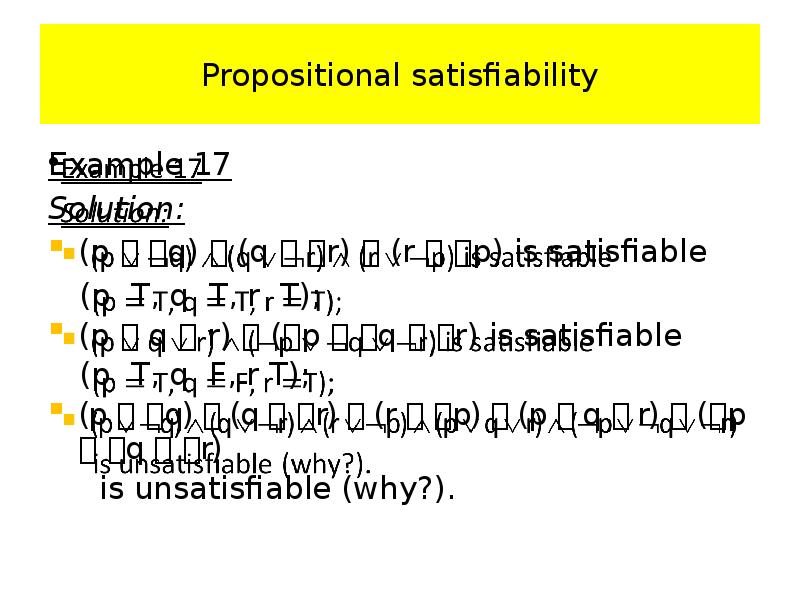
- 99. Propositional satisfiability Example 17 Determine whether each of the compound propositions
- 100. Propositional satisfiability Example 17 Solution: (p q) (q
- 101. Satisfiability problem Many problems, in diverse areas such as robotics,
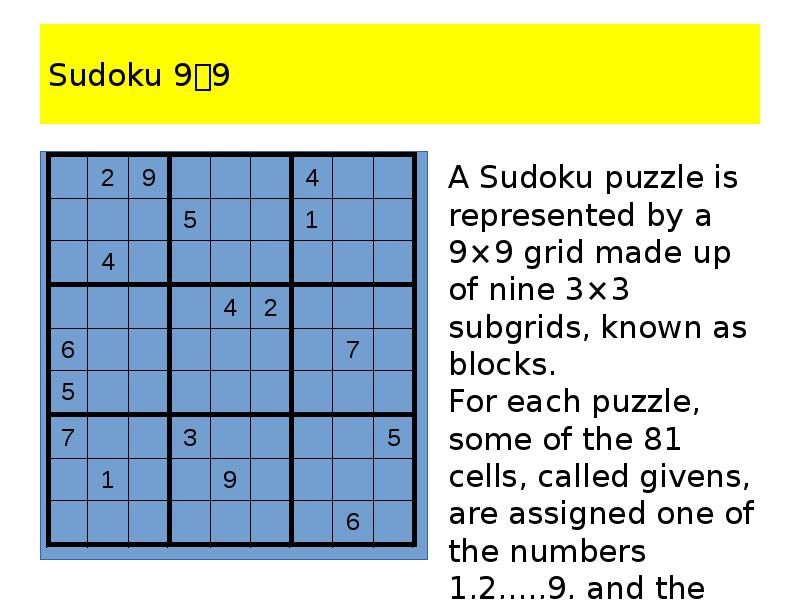
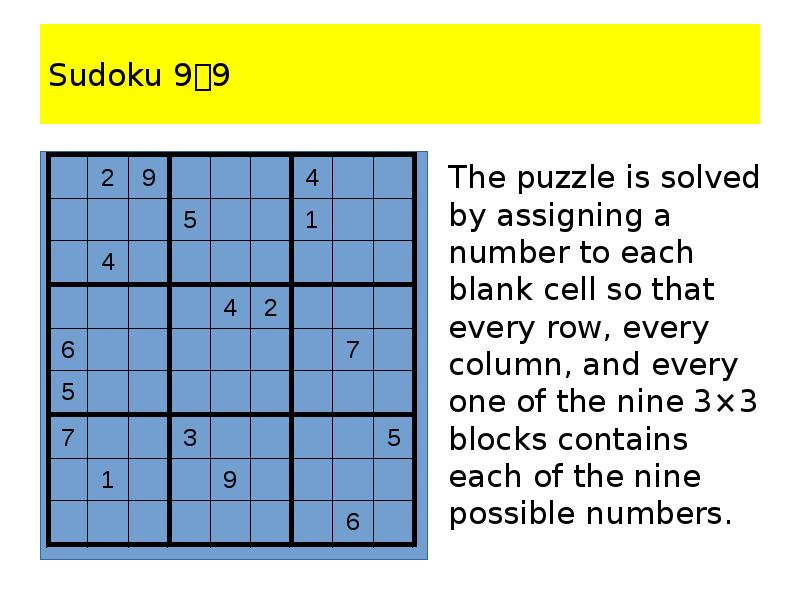
- 102. Sudoku 99 A Sudoku puzzle is represented by a 9×9 grid
- 103. Sudoku 99 The puzzle is solved by assigning a number to
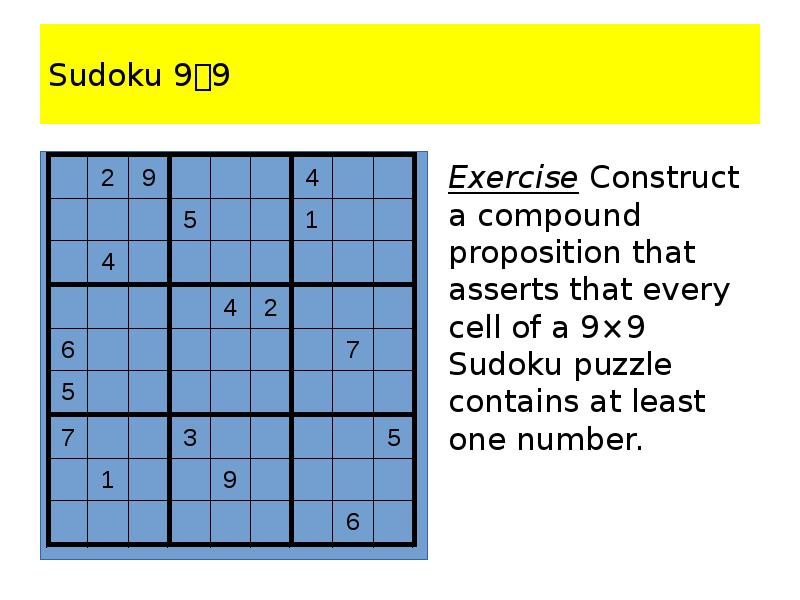
- 104. Sudoku 99 Exercise Construct a compound proposition that asserts that every
- 105. Скачать презентацию







































































Слайды и текст этой презентации
Похожие презентации