Rotation of rigid bodies. Angular momentum and torque. Properties of fluids презентация

Physics 1 Voronkov Vladimir Vasilyevich

Lecture 4 Rotation of rigid bodies. Angular momentum and torque. Properties of fluids.

Rotation of Rigid Bodies in General case When a rigid object is rotating about a fixed axis, every particle of the object rotates through the same angle in a given time interval and has the same angular speed and the same angular acceleration. So the rotational motion of the entire rigid object as well as individual particles in the object can be described by three angles. Using these three angles we can greatly simplify the analysis of rigid-object rotation.

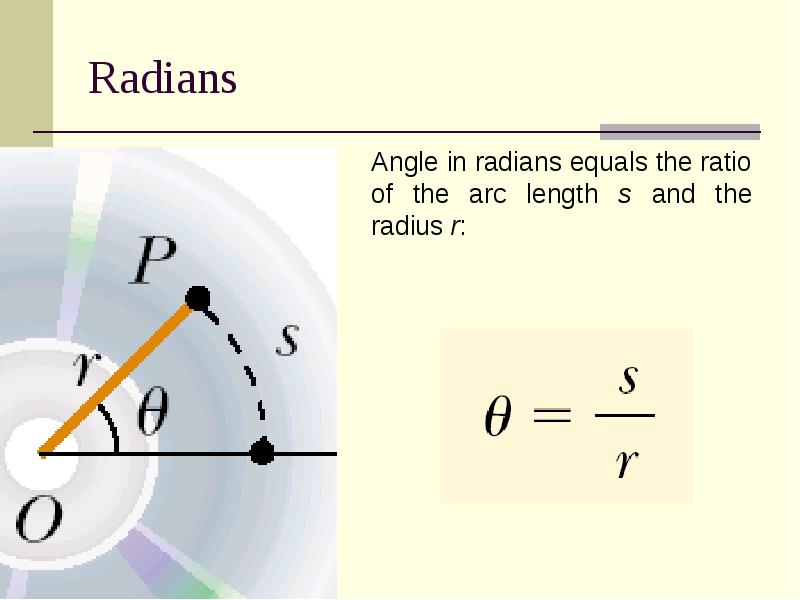
Radians Angle in radians equals the ratio of the arc length s and the radius r:

Angular kinematics Angular displacement: Instantaneous angular speed: Instantaneous angular acceleration:

Angular and linear quantities Every particle of the object moves in a circle whose center is the axis of rotation. Linear velocity: Tangential acceleration: Centripetal acceleration:

Total linear acceleration Tangential acceleration is perpendicular to the centripetal one, so the magnitude of total linear acceleration is

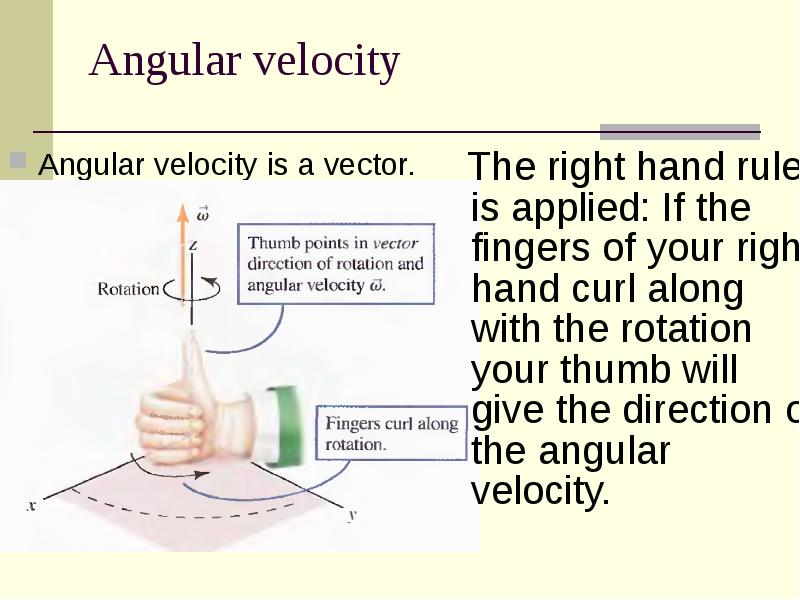
Angular velocity Angular velocity is a vector.

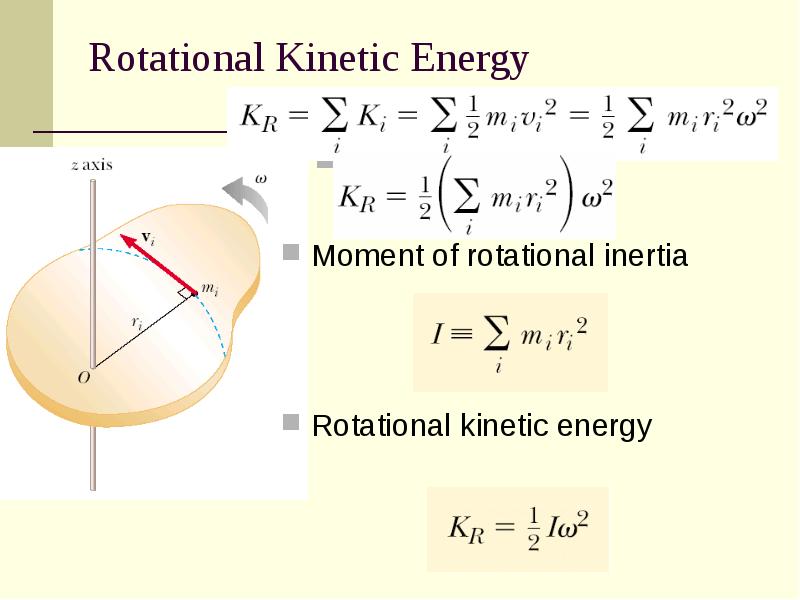
Rotational Kinetic Energy

Calculations of Moments of Inertia

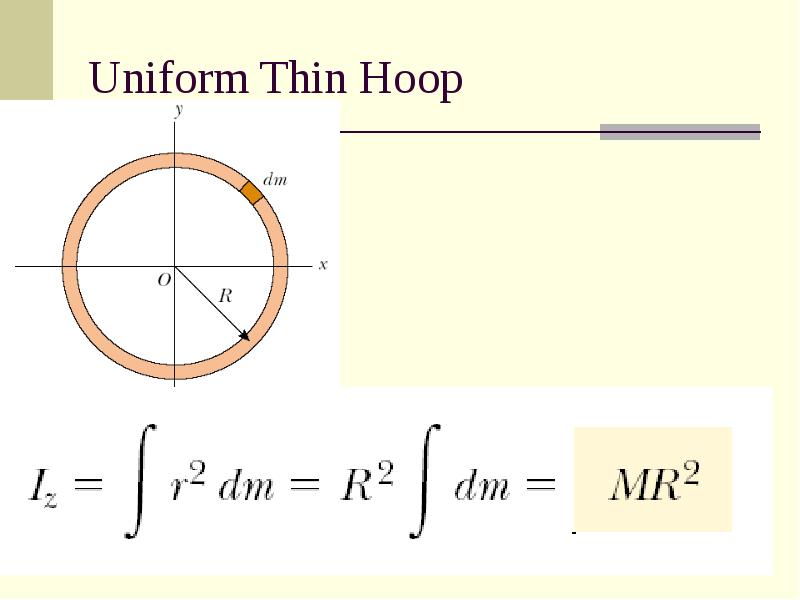
Uniform Thin Hoop

Uniform Rigid Rod

Uniform Solid Cylinder

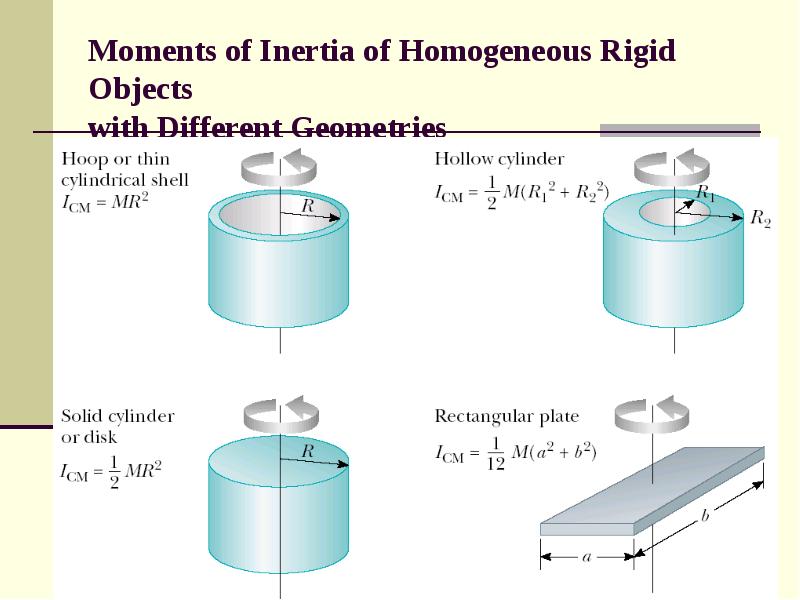
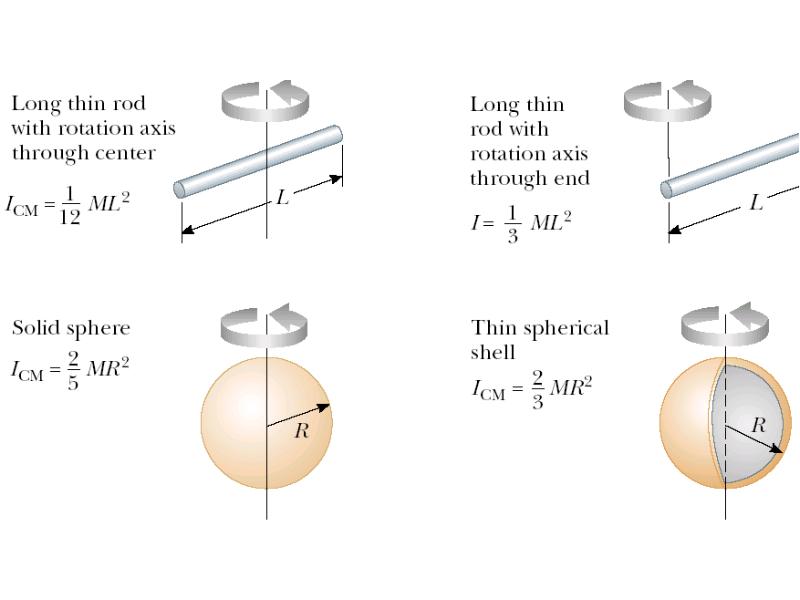
Moments of Inertia of Homogeneous Rigid Objects with Different Geometries

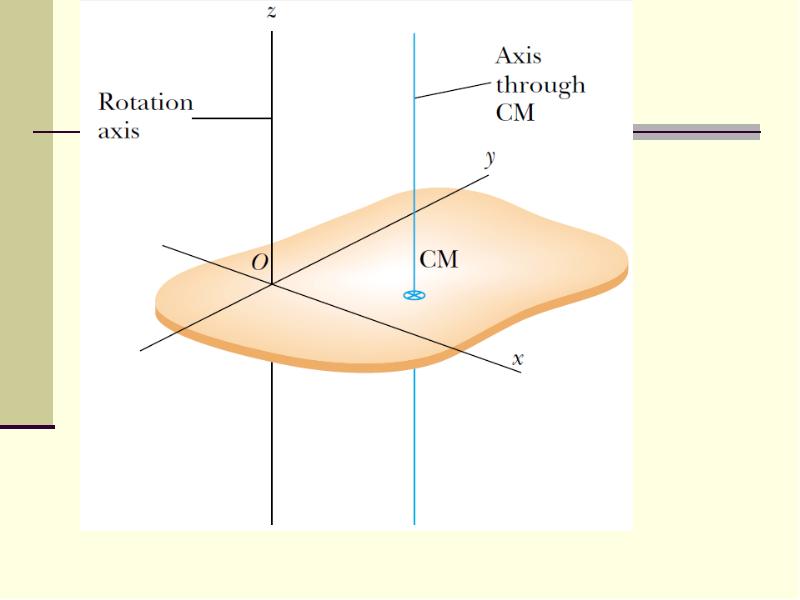
Parallel-axis theorem Suppose the moment of inertia about an axis through the center of mass of an object is ICM. Then the moment of inertia about any axis parallel to and a distance D away from this axis is

Torque When a force is exerted on a rigid object pivoted about an axis, the object tends to rotate about that axis. The tendency of a force to rotate an object about some axis is measured by a vector quantity called torque  (Greek tau).

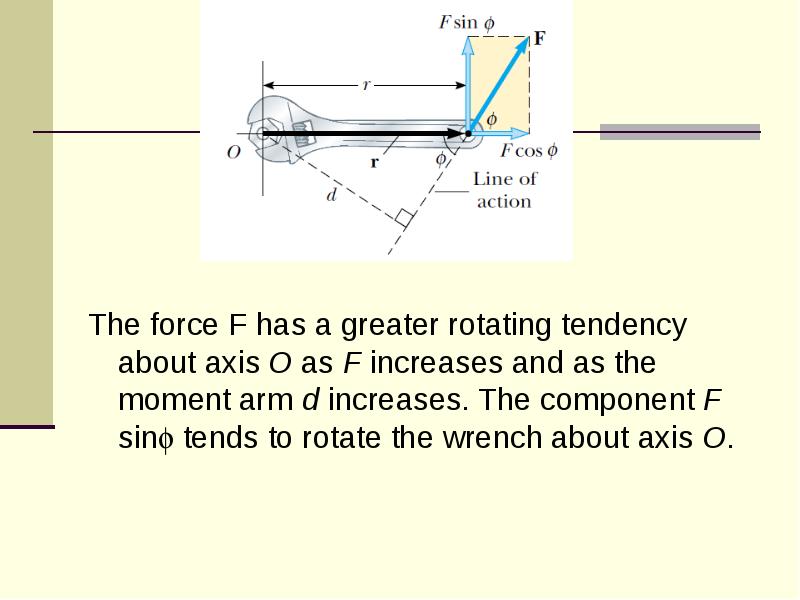
The force F has a greater rotating tendency about axis O as F increases and as the moment arm d increases. The component F sin tends to rotate the wrench about axis O.

We use the convention that the sign of the torque resulting from a force is positive if the turning tendency of the force is counterclockwise and is negative if the turning tendency is clockwise. Then

Torque is not Force Torque is not Work Torque should not be confused with force. Forces can cause a change in linear motion, as described by Newton’s second law. Forces can also cause a change in rotational motion, but the effectiveness of the forces in causing this change depends on both the forces and the moment arms of the forces, in the combination that we call torque. Torque has units of force times length: newton · meters in SI units, and should be reported in these units. Do not confuse torque and work, which have the same units but are very different concepts.

Rotational Dynamics Let’s add which equals zero, as and are parallel. Then: So we get

Rotational analogue of Newton’s second law Quantity L is an instantaneous angular momentum. The torque acting on a particle is equal to the time rate of change of the particle’s angular momentum.

Net External Torque The net external torque acting on a system about some axis passing through an origin in an inertial frame equals the time rate of change of the total angular momentum of the system about that origin:

Angular Momentum of a Rotating Rigid Object Angular momentum for each particle of an object: Angular momentum for the whole object: Thus:

Angular acceleration

The Law of Angular Momentum Conservation The total angular momentum of a system is constant if the resultant external torque acting on the system is zero, that is, if the system is isolated.

Change in internal structure of a rotating body can result in change of its angular velocity.

When a rotating skater pulls his hands towards his body he spins faster.

Three Laws of Conservation for an Isolated System Full mechanical energy, linear momentum and angular momentum of an isolated system remain constant.

Work-Kinetic Theory for Rotations Similarly to linear motion:

The net work done by external forces in rotating a symmetric rigid object about a fixed axis equals the change in the object’s rotational energy.

Equations for Rotational and Linear Motions

Independent Study for IHW2 Vector multiplication (through their components i,j,k).Right-hand rule of Vector multiplication. Elasticity Demonstrate by example and discussion your understanding of elasticity, elastic limit, stress, strain, and ultimate strength. Write and apply formulas for calculating Young’s modulus, shear modulus, and bulk modulus. Units of stress.

Fluids Fluids Define absolute pressure, gauge pressure, and atmospheric pressure, and demonstrate by examples your understanding of the relationships between these terms. Pascal’s law. Archimedes’s law. Rate of flow of a fluid. Bernoulli’s equation. Torricelli’s theorem.

Literature to Independent Study Lecture on Physics Summary by Umarov. (Intranet) Fishbane Physics for Scientists… (Intranet) Serway Physics for Scientists… (Intranet)

Problems A solid sphere and a hollow sphere have the same mass and radius. Which momentum of rotational inertia is higher if it is? Prove your answer with formulae. What are the units for, are these quantities vectors or scalars: Angular momentum Angular kinetic energy Angular displacement Tangential acceleration Angular acceleration Torque