Численное интегрирование и его погрешности. Методы прямоугольников и трапеций. Метод Симпсона. Правило Рунге. (Лекция 5) презентация
Содержание
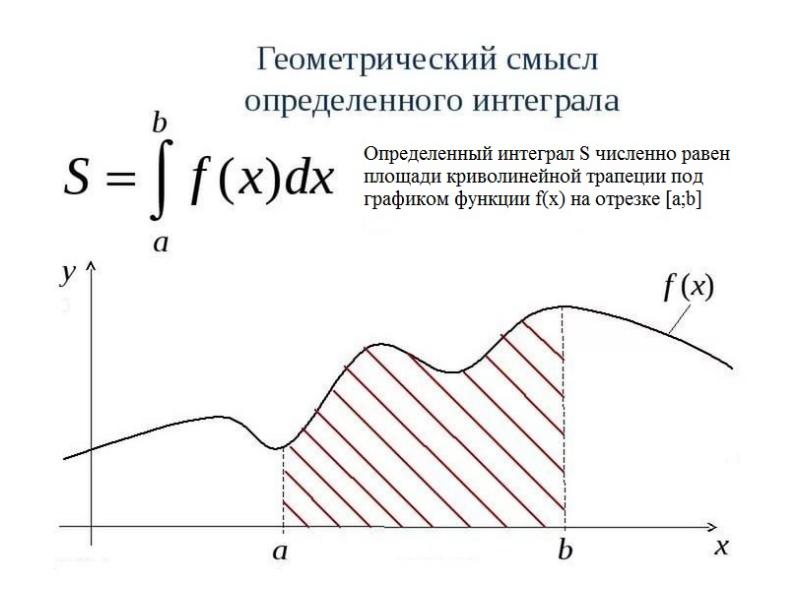
- 2. Определенный интеграл Из курса математического анализа известно, что, если функция f(x)
- 3. Методы интегрирования
- 5. Приближенное вычисление площади криволинейной трапеции Для приближенного вычисления этой площади отрезок
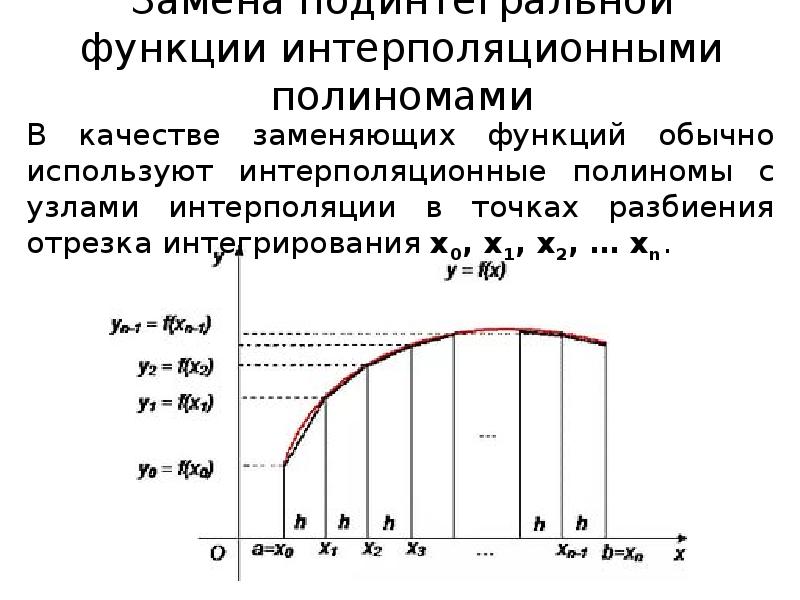
- 6. Замена подинтегральной функции интерполяционными полиномами
- 7. Методы численного интегрирования Для получения простых формул используют полиномы нулевой, первой
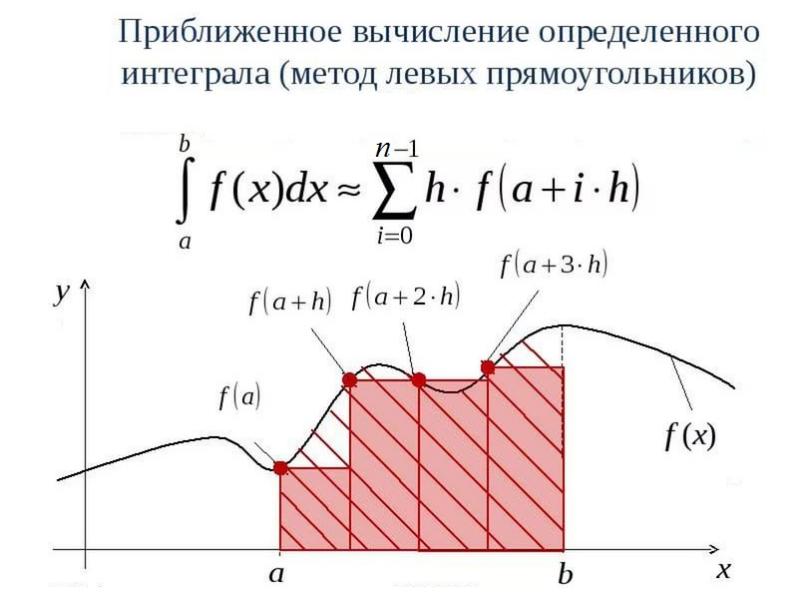
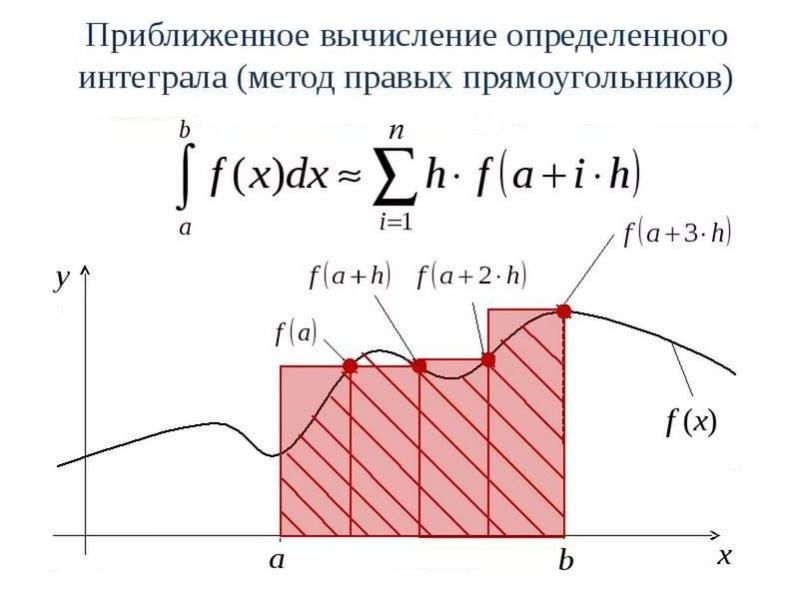
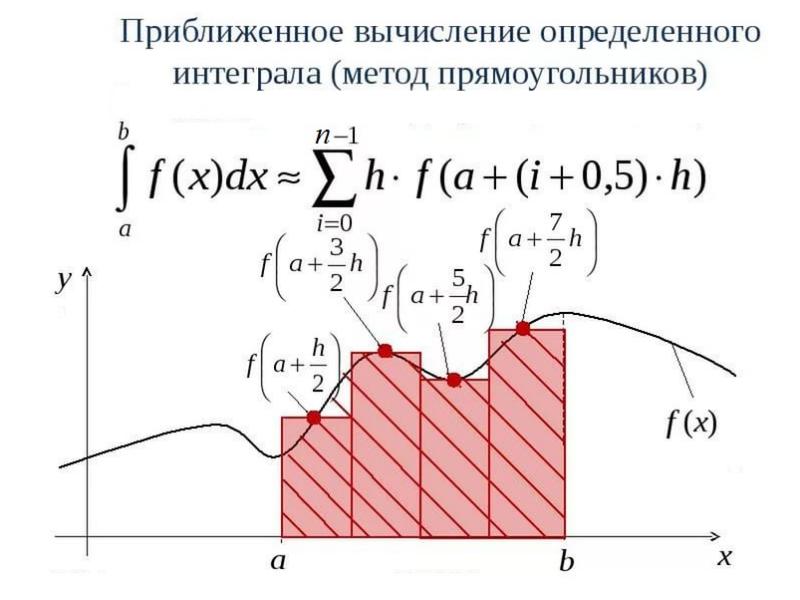
- 8. Методы прямоугольников В методах прямоугольников подинтегральная функция f(x) заменяется в пределах
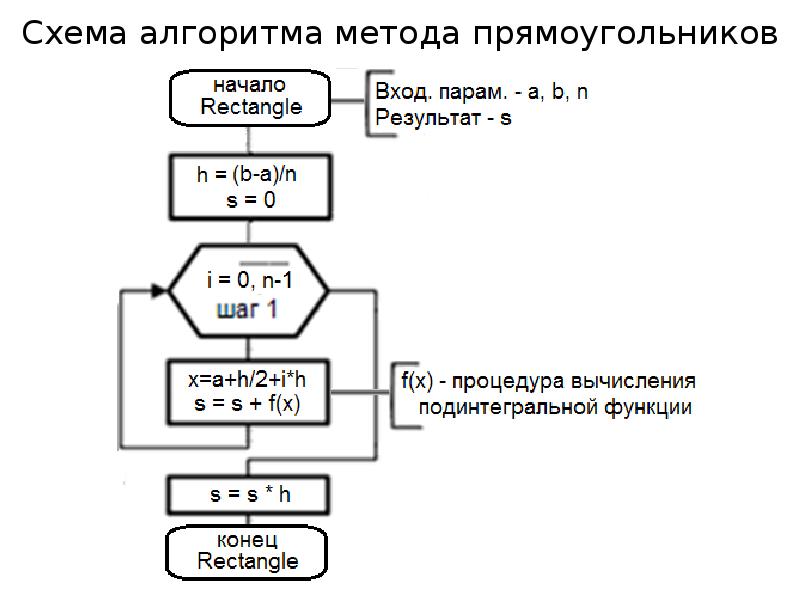
- 12. Схема алгоритма метода прямоугольников
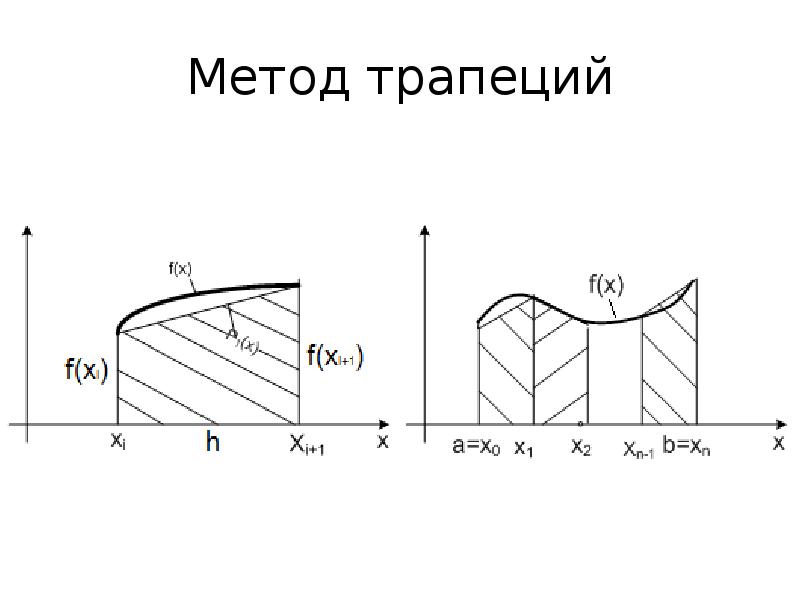
- 13. Метод трапеций В методе трапеций подинтегральная функция f(x) на каждом элементарном
- 14. Метод трапеций
- 15. Вывод формулы трапеций
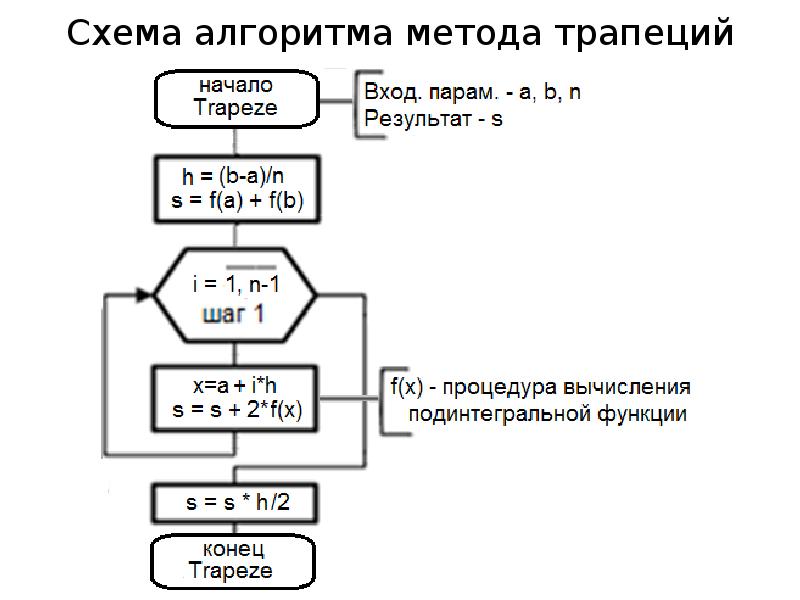
- 16. Схема алгоритма метода трапеций
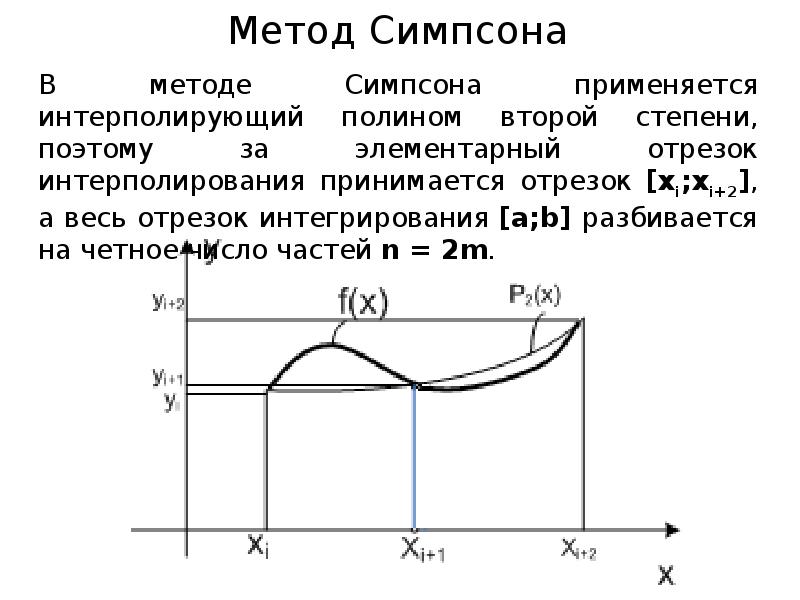
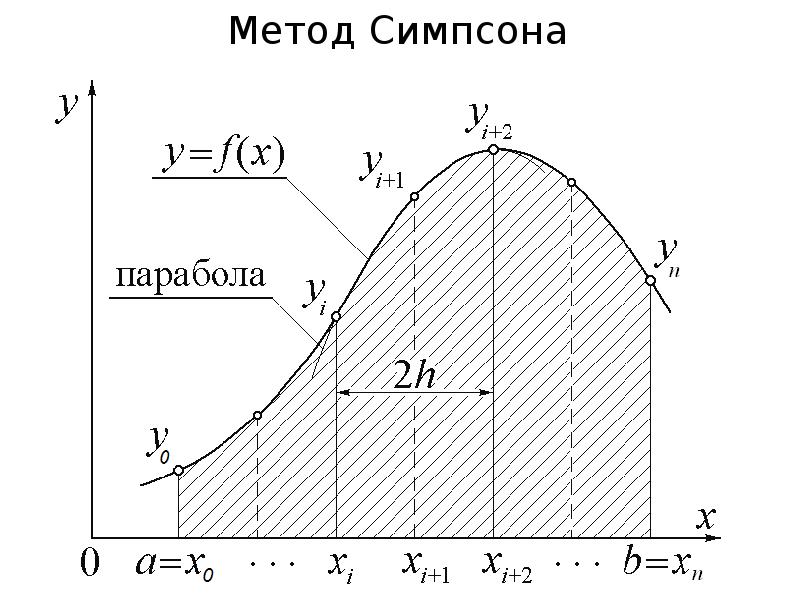
- 17. Метод Симпсона
- 18. Метод Симпсона
- 19. Вывод формулы Симпсона
- 20. Вывод формулы Симпсона
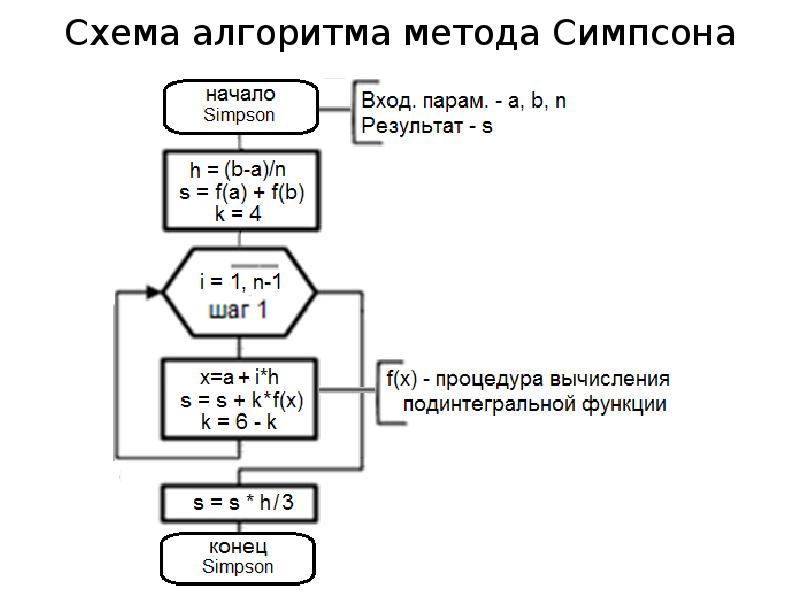
- 21. Схема алгоритма метода Симпсона
- 22. Погрешности численного интегрирования Замена подинтегральной функции интерполяционным полиномом приводит к погрешности
- 23. Оценки погрешности численного интегрирования
- 24. Сравнение погрешностей методов Из приведенных формул видно, что уменьшение шага интегрирования
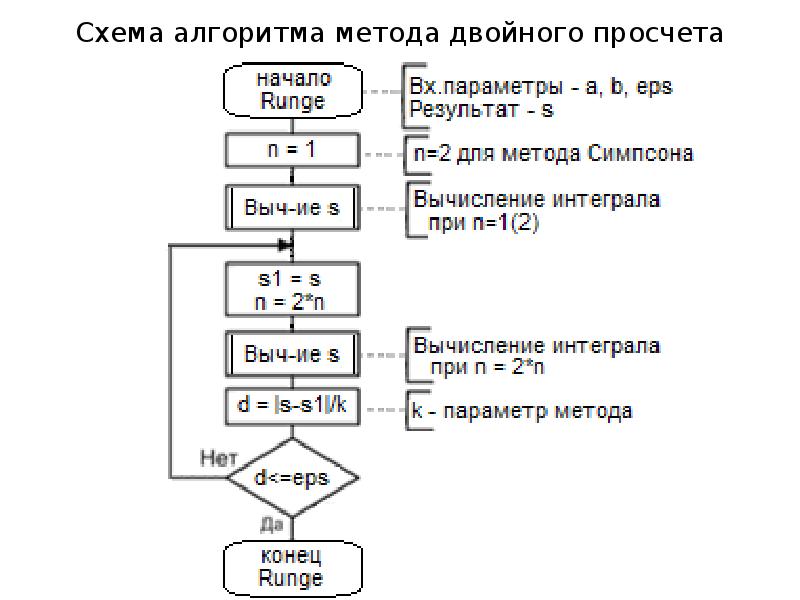
- 25. Метод двойного просчета (правило Рунге)
- 26. Схема алгоритма метода двойного просчета
- 27. Скачать презентацию














Слайды и текст этой презентации
Скачать презентацию на тему Численное интегрирование и его погрешности. Методы прямоугольников и трапеций. Метод Симпсона. Правило Рунге. (Лекция 5) можно ниже:
Похожие презентации





























