Числовые множества презентация

ЧИСЛОВЫЕ МНОЖЕСТВА 1. N, Z, Q, I, R, RR, C. 2. Подмножества вещественных чисел: Пусть . Отрезок, сегмент: ; Интервал: ; Полуинтервал: , ; Замкнутый луч: , ; Открытый луч: , . Определение. Пусть a  R,  > 0. Интервал (a – , a + ) будем называть -окрестностью точки a . Обозначение: U(a,)= (a – , a+)= {x  R | |x – a|<}.

ЧИСЛОВЫЕ МНОЖЕСТВА R  +, – = Пусть  > 0. Тогда U(+,) = (1/; +)  + = x : x > 1/ ; U(–,) = (–; –1/)  – = x : x < – 1/ ; U(,) = (–; –1/)  (1/; +) = x : |x|> 1/ .

АБСОЛЮТНАЯ ВЕЛИЧИНА ЧИСЛА Для любого числа x  R неотрицательное число называется абсолютной величиной или модулем числа x ( ). |x| ≥ 0. |x| = |– x|. – |x| ≤ x ≤ |x|. Пусть   R,  > 0. Тогда неравенства |x| ≤  и –  ≤ x ≤  – равносильны. |x + y| ≤ |x| + |y|. |x – y| ≥ |x| – |y|. |x  y| = |x|  |y| и , если y  0.

ГРАНИ ЧИСЛОВЫХ МНОЖЕСТВ Определение. Множество А называется ограниченным сверху (снизу), если существует такое действительное число М (число m), что каждый элемент x  A удовлетворяет неравенству x  M (x  m). При этом число М (число m) называют верхней (нижней) гранью множества А. Определение. Множество, ограниченное сверху и снизу называется ограниченным. Определение. Наименьшая из всех верхних граней ограниченного сверху множества называется точной верхней гранью. Обозначение: М=sup A или . Наибольшая из всех нижних граней ограниченного снизу множества называется точной нижней гранью. Обозначение: m=inf A или . Теорема (Больцано). Любое ограниченное сверху (снизу), непустое числовое множество имеет точную верхнюю (нижнюю) грань.

ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ Определение. Числовой последовательностью {xn} называется упорядоченное счетное множество чисел {x1,x2,x3,x4,...}. Определение. Числовой последовательностью {xn} называют отображение, действующее из N в R т.е. xn = f (n). Числа {xn}, где n=1,2,3,… – элементы (члены) последовательности, символ xn – общий член последовательности, а число n – его номер.

АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ Пусть даны две последовательности {xn} и {yn}. Произведением последовательности {xn} на число c называется последовательность вида: . Суммой последовательности {xn} и {yn} называется последова-тельность вида: {xn} + {yn} = {x1 + y1; x2 + y2; …; xn + yn; …} Разностью – последовательность вида: {xn} – {yn} = {x1 – y1; x2 – y2; x3 – y3; …; xn – yn; …}. Произведением – последовательность вида: {xn}  {yn} = {x1  y1; x2  y2; x3  y3; …; xn  yn; …}. Частным – последовательность вида .

ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ Определение. Последовательность называется  ограниченной сверху, если ;  ограниченной снизу, если ;  ограниченной, если ;  неограниченной, если ;  возрастающей, если ;  неубывающей, если ;  убывающей, если ; невозрастающей, если .

ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ Определение. Число а называется пределом последовательности {xn}, если для любого положительного числа  существует номер N такой, что при n > N выполняется неравенство | xn  a| <  . Обозначение.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ Геометрическая интерпретация того, что состоит в следующем: «Какого бы ни было положительное число , все элементы последовательности, начиная с некоторого номера N+1, находятся внутри -окрестности точки а».

Бесконечно малые и бесконечно большие последовательности Определение. Последовательность {xn} называется бесконечно малой последовательностью (б.м.п.), если для любого положительного числа  существует номер N такой, что при n > N выполняется неравенство |x n | <  . Определение. Последовательность {xn} называется бесконечно большой последовательностью (б.б.п.), если для любого положительного числа A существует номер N такой, что при n > N выполняется неравенство |x n | > A. Теорема. Если {xn} – б.м.п. и все ее члены отличны от нуля, то {1/xn} – б.б.п., и обратно, если {xn}  б.б.п., тогда {1/xn} – есть б.м.п.

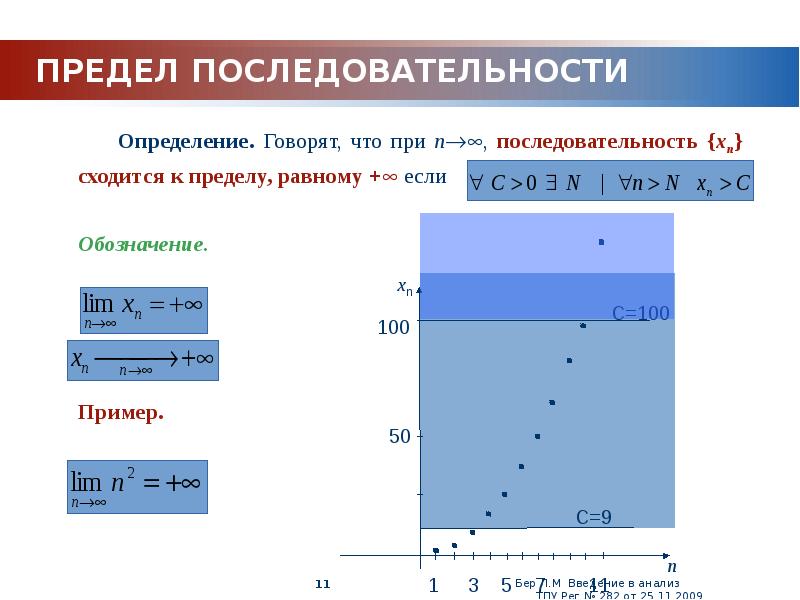
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ Определение. Говорят, что при n, последовательность {xn} сходится к пределу, равному + если Обозначение. Пример.

ОСНОВНЫЕ СВОЙСТВА Б.М.П. 1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность. Следствие. Сумма и разность любого конечного числа б.м.п. есть также б.м.п. 2. Произведение двух б.м.п. есть б.м.п. Следствие. Произведение любого конечного числа б.м.п. есть также б.м.п. 3. Произведение б.м.п. на ограниченную последовательность есть б.м.п. Следствие. Произведение б.м.п. на число есть б.м.п. 4. Б.м.п. ограничена.

ОСНОВНЫЕ СВОЙСТВА Б.Б.П. Если xn - ограничена, а yn такая, что , то а) ; б) ; в) , если yn  0 для любого n. Если , , то а) ; б) . Если , , то а) ; б) . Если , a  R, a  0, , то Если , a  0, , то

СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Теорема 1. (о единственности предела). Если последо-вательность имеет предел, то он единственный. Теорема 2. Для того, чтобы последовательность {xn} была сходящейся , необходимо и достаточно, чтобы ее можно было представить в виде x n = a + n , где , а  , а {n} б.м.п. Теорема 3. Сходящаяся последовательность ограничена. Теорема 4. Сумма (разность) двух сходящихся последо-вательностей {xn} и {yn} есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей .

СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Теорема 5. Произведение двух сходящихся последо-вательностей {xn} и {yn} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей . Теорема 6. Частное двух сходящихся последовательностей {xn} и {yn} при условии, что для всех n выполняется неравенство yn  0 и предел {yn} отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}

СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Теорема 7. Пусть {xn} сходящаяся последовательность и . Тогда . Следствие. Если {xn} и {yn} сходящиеся последовательности и , то . Теорема 8. Пусть {xn}, {yn} и {zn} – последовательности, и 1.  {xn} и {zn} и сходящиеся последовательности; 2. ; 3.   . Тогда {yn} также сходящаяся последовательность и .

МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ Числовая последовательность называется {xn} называется  возрастающей, если ;  строго возрастающей, если ;  убывающей, если ; строго убывающей, если . Убывающие и возрастающие последовательности называются монотонными, а строго убывающие и строго возрастающие последовательности называются строго монотонными.

МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ Теорема 9. (Вейерштрасса) Всякая возрастающая числовая последовательность {xn} имеет предел: конечный, если она ограниченна сверху, и бесконечный, если она неограниченна сверху, причем Аналогично, если {xn} – убывающая последовательность, то существует (конечный или бесконечный) предел и, следовательно, этот предел конечен, если последовательность ограниченна снизу, и бесконечный, если она неограниченна снизу.

КРИТЕРИЙ КОШИ Теорема 10 (Критерий Коши). Для того чтобы последовательность {xn} сходилась к конечному пределу, необходимо и достаточно, чтобы . Последовательность, удовлетворяющая этому условию называется «фундаментальной последовательностью» или последовательностью, «сходящейся в себе».

Спасибо за внимание