Дискретная математика презентация
Содержание
- 2. Справочные данные Кафедра АИВС (Автоматизированных информационных и вычислительных систем) Преподаватель Мякушко
- 3. Введение Дискре́тная матема́тика — часть математики, изучающая дискретные математические структуры, такие, как графы
- 4. Введение Дискретная математика – математический аппарат, заложенный в основу работы всех
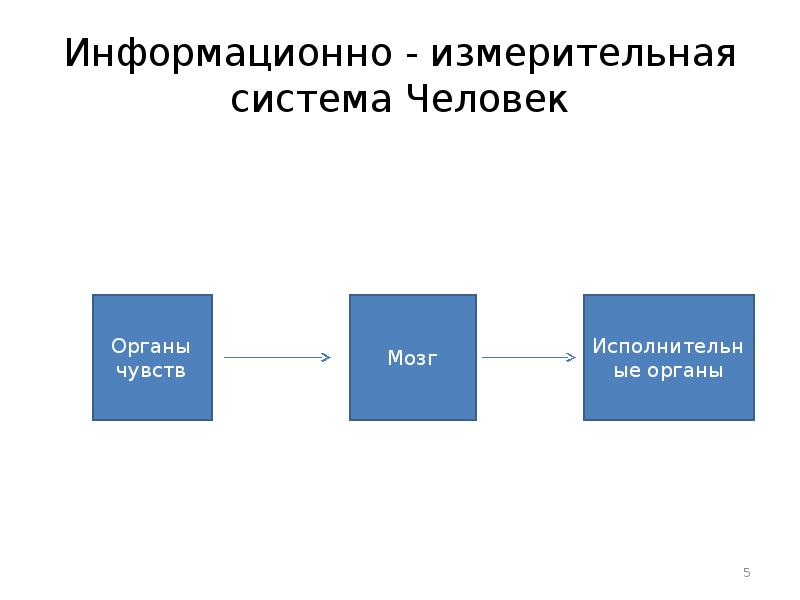
- 5. Информационно - измерительная система Человек
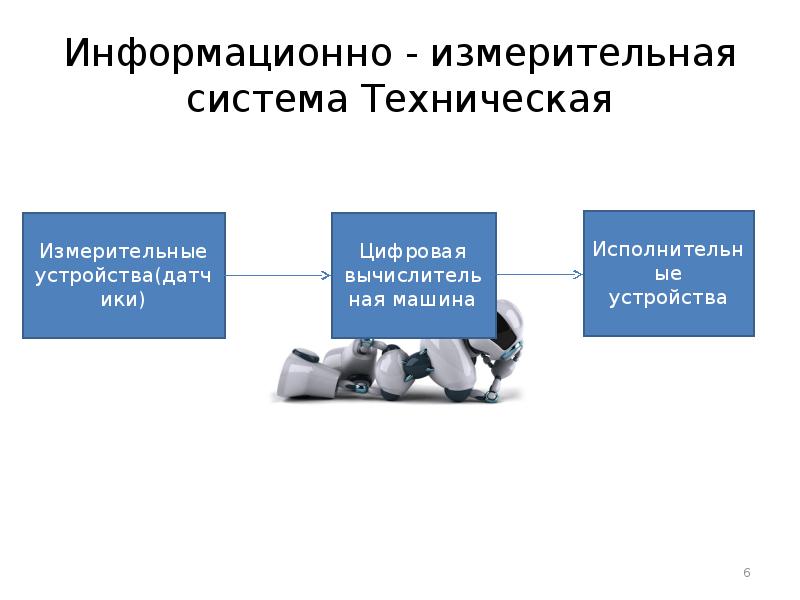
- 6. Информационно - измерительная система Техническая
- 7. Восприятие внешнего мира информационно – измерительными системами Объекты который присутствуют вокруг
- 8. Мое личное определение, что есть множество. Множество – это совокупность различных
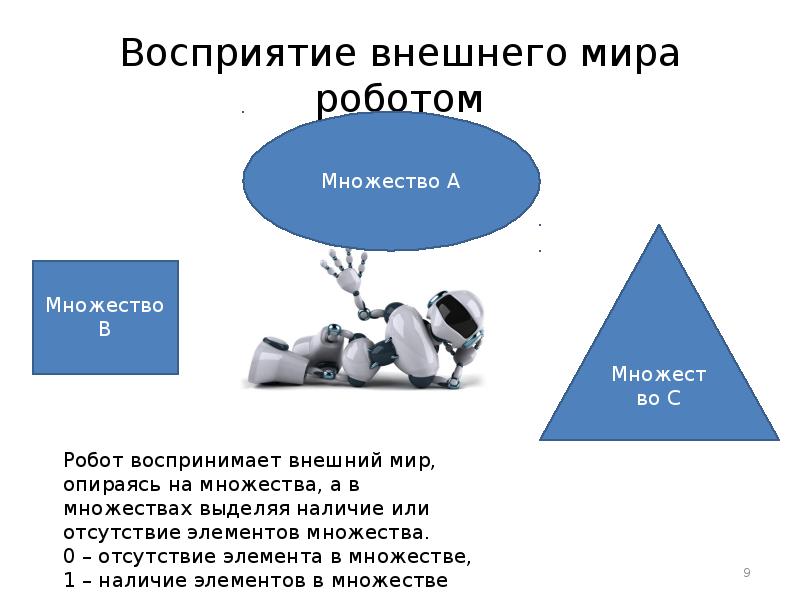
- 9. Восприятие внешнего мира роботом
- 11. Формальное представление множеств А = {a, b, c, d} a ∈
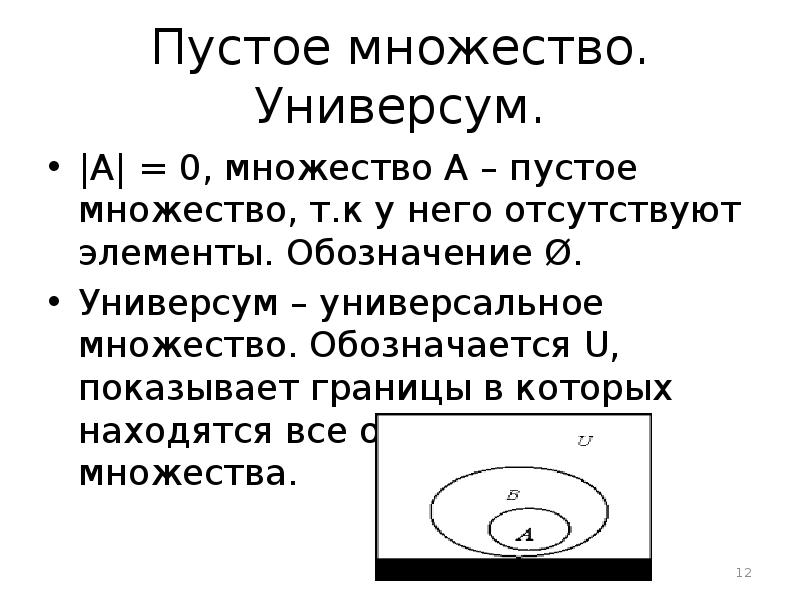
- 12. Пустое множество. Универсум. |A| = 0, множество А – пустое множество,
- 13. Множество. Вектор. A= {a,b,c,d},элементы множества можно перемещать. Важно наличие элемента, а
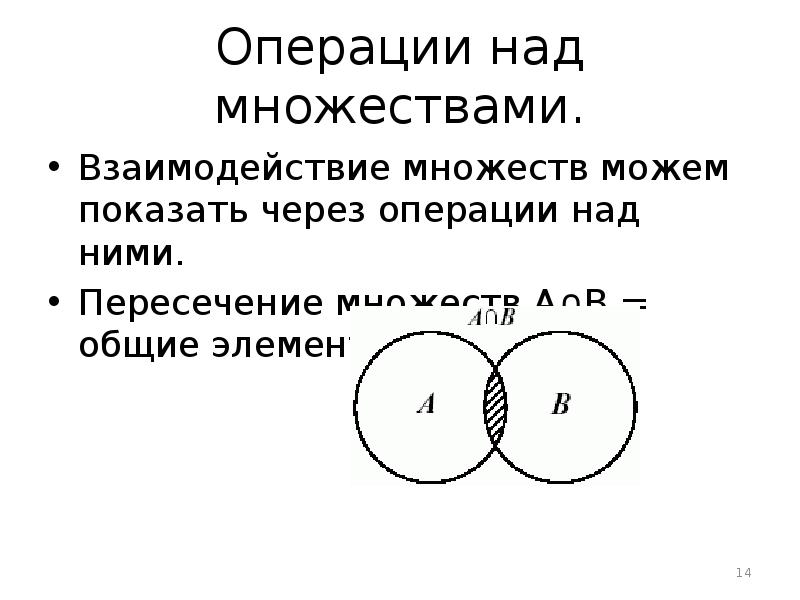
- 14. Операции над множествами. Взаимодействие множеств можем показать через операции над ними.
- 15. Пример пересечения множеств. |U| = 10, |A| = 8, |B| =
- 16. Объединение множеств. |U| = 10, |A| = 8, |B| = 5
- 17. Дополнение. Дополнение – это элементы которые не достают до универсума |U|
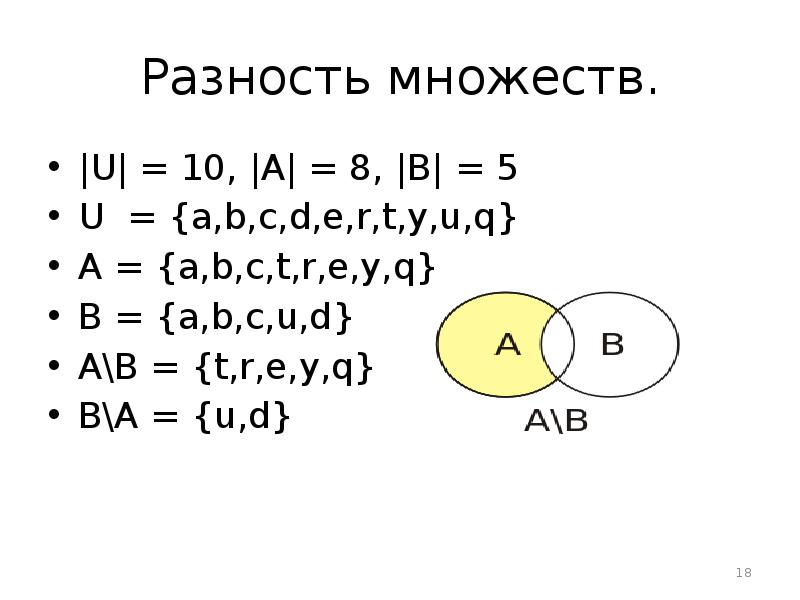
- 18. Разность множеств. |U| = 10, |A| = 8, |B| = 5
- 19. Симметрическая разность. |U| = 10, |A| = 8, |B| = 5
- 20. Самостоятельная работа.
- 21. Множество подмножеств.(Булеан) A = {x,y,z} β(A) – множество подмножеств β(A) =
- 22. Взаимно – однозначные соответствия Булеана и множества двоичных векторов β(A) =
- 23. Пример A = {a,b,c,d} β(A) = Ø↔(0,0,0,0,) {a,b,c,d} ↔(1,1,1,1) {a,b} ↔(1,1,0,0)
- 24. Взаимодействие объектов показывается через операции над подмножествами β(A) = Ø↔(0,0,0)
- 25. Пример №2 A = {a,b,c,d} β(A) = Ø↔(0,0,0,0) {a,b,c,d} ↔(1,1,1,1) {a,b}∩{c,d}
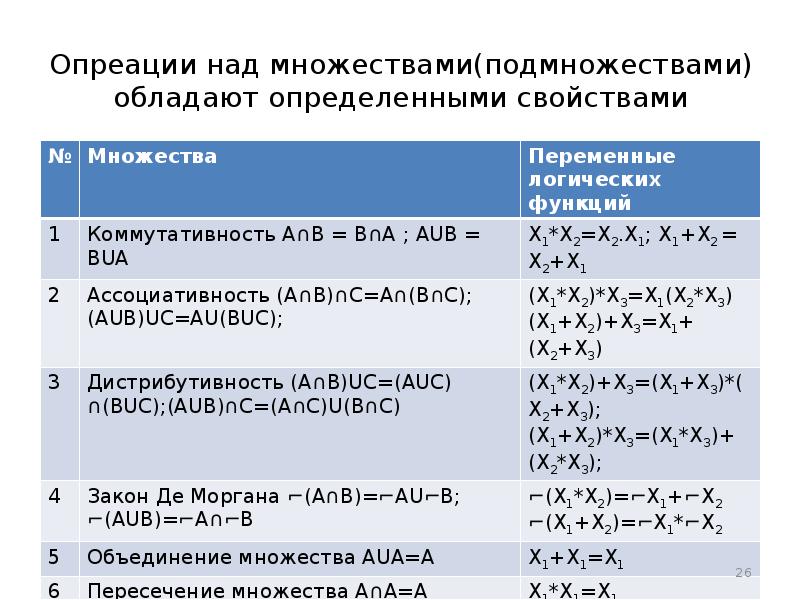
- 26. Опреации над множествами(подмножествами) обладают определенными свойствами
- 27. Взаимно – однозначные соответствия для построения цифровых технических систем (β(A), U,
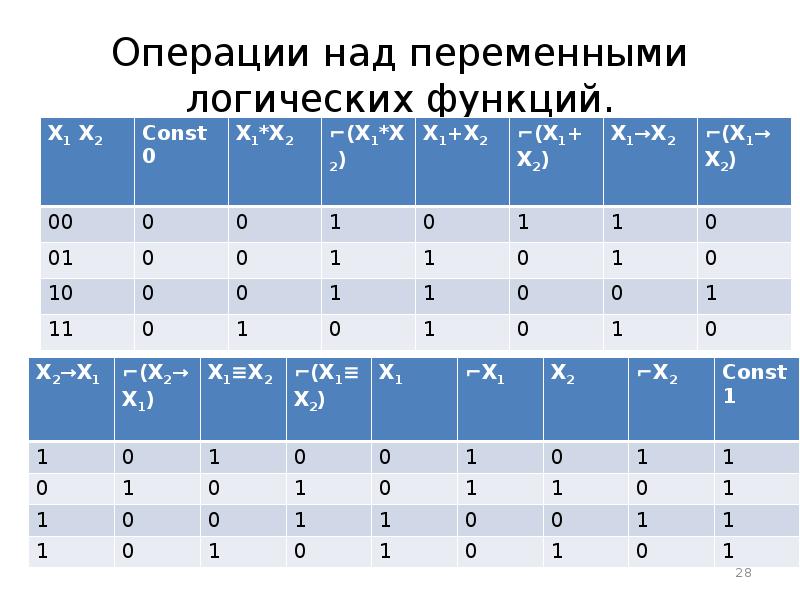
- 28. Операции над переменными логических функций.
- 29. Отношения
- 30. Графическое изображение отношений (граф) . . . .
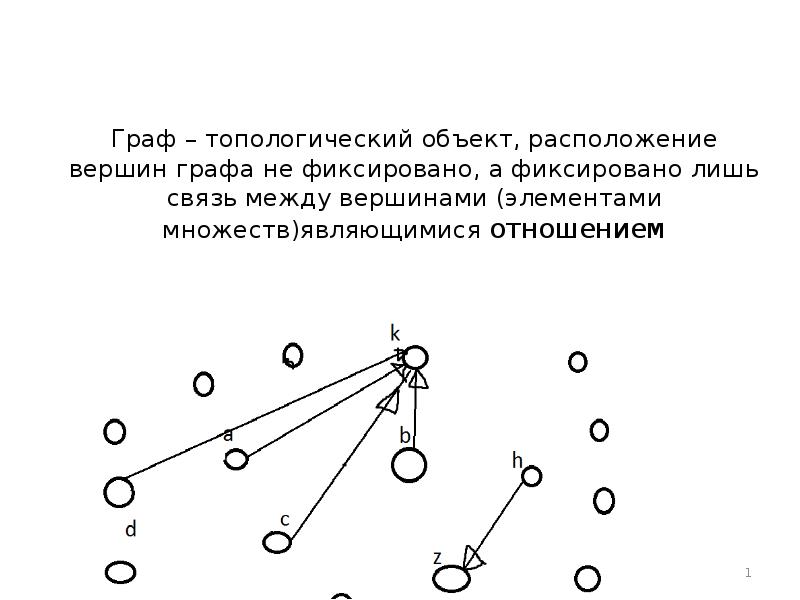
- 31. Граф – топологический объект, расположение вершин графа не фиксировано, а фиксировано
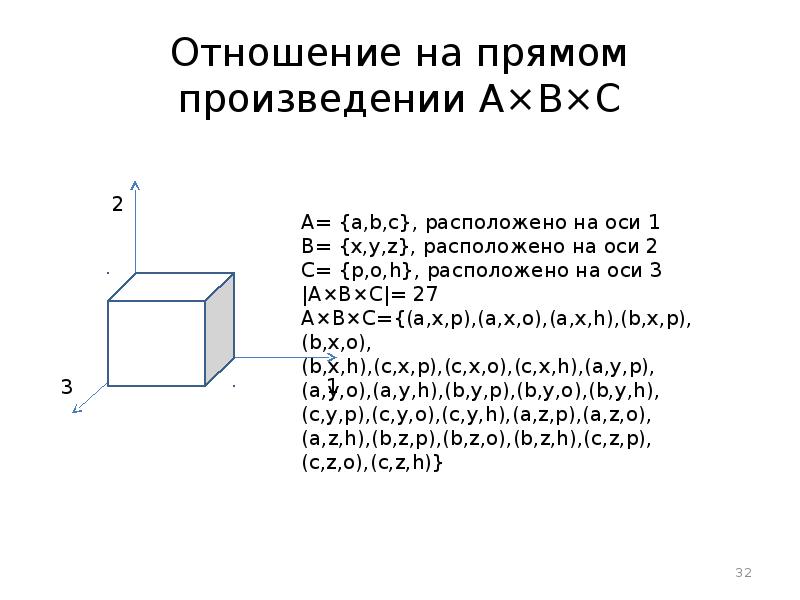
- 32. Отношение на прямом произведении A×B×C
- 33. Примеры отношения на прямом произведении A×B×C R⊆A×B×C |R|=8, R ={(a,x,p),(a,x,o),(a,x,h),(b,x,p),(b,x,o), (b,x,h),(c,x,p),(c,x,o)}
- 34. Операции над отношениями R1⊆A×B, |A| = 5, |B| = 5, A
- 35. Обратное отношение. R-1 – обозначение обратного отношения. R = {(a,b),(c,d),(e,f),(i,j)} R-1
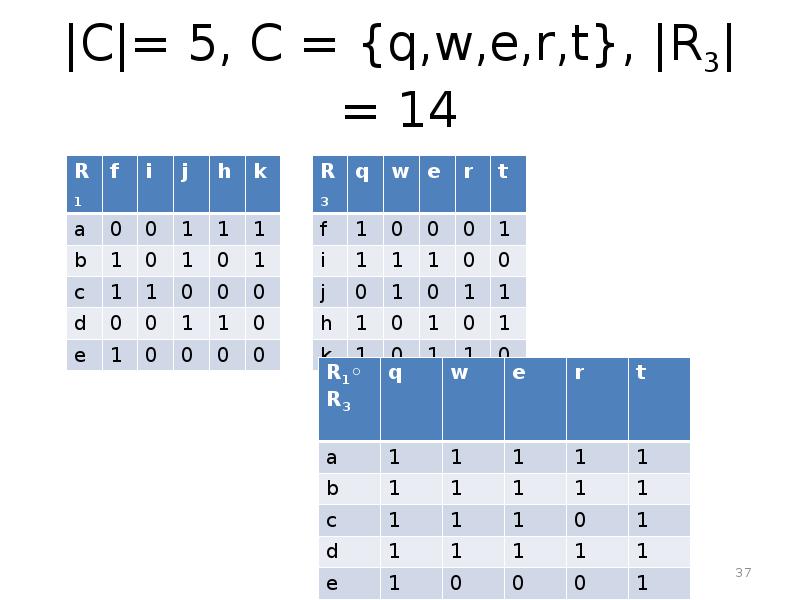
- 36. Композиция отношений. R1⊆A×B R3⊆B×C R1⊆A×B R1 ◦ R3 - обозначение операции.
- 37. |C|= 5, C = {q,w,e,r,t}, |R3|= 14
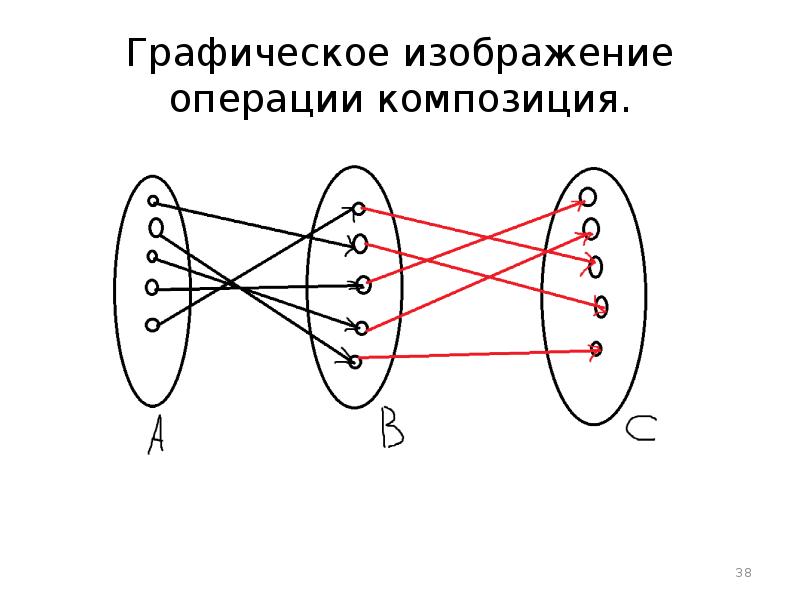
- 38. Графическое изображение операции композиция.
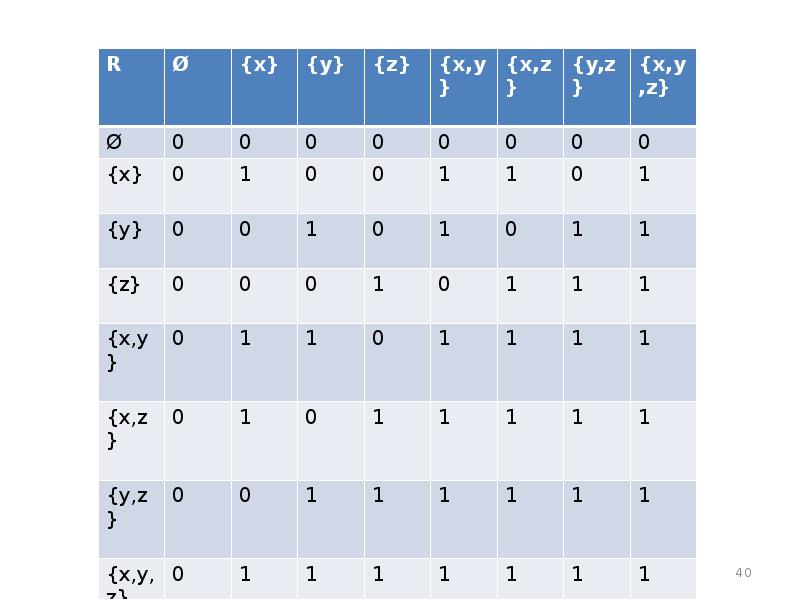
- 39. Отношения на прямом произведении Булеана. R⊆β(A) × β(A), где А =
- 41. Контрольная работа №2 R1⊆A×B R2⊆A×B R3⊆B×C |A|=|B|=|C|=10;| R1 | = 70,
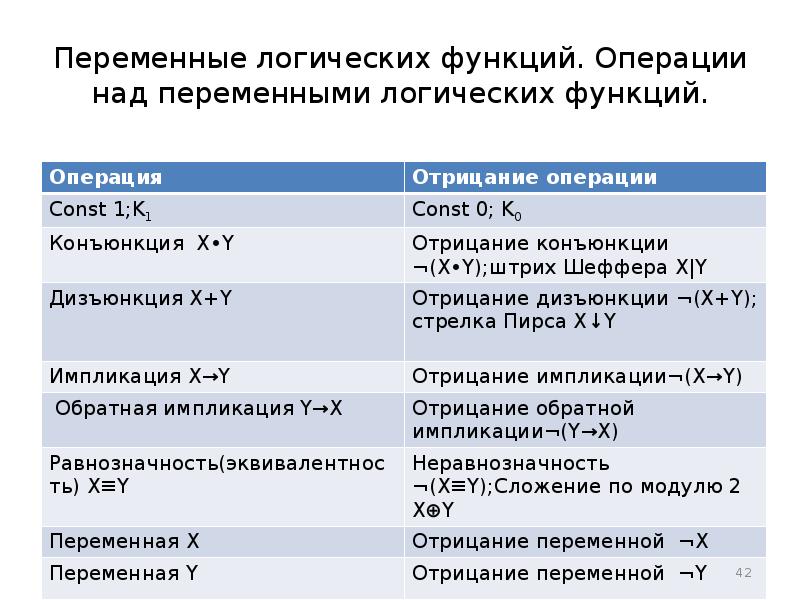
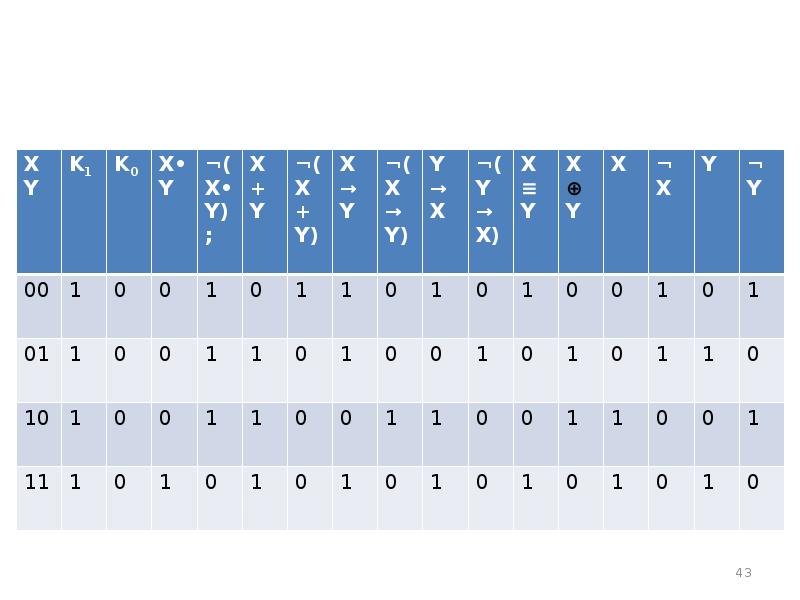
- 42. Переменные логических функций. Операции над переменными логических функций.
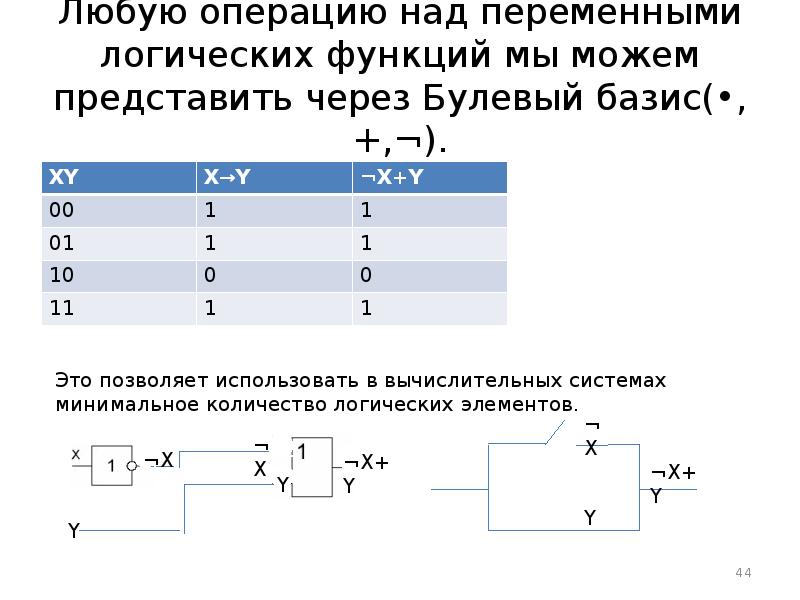
- 44. Любую операцию над переменными логических функций мы можем представить через Булевый
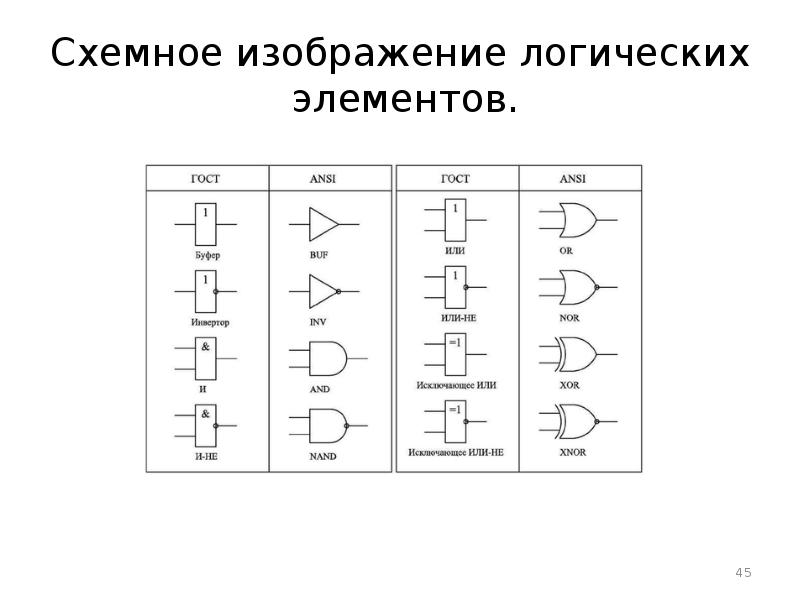
- 45. Схемное изображение логических элементов.
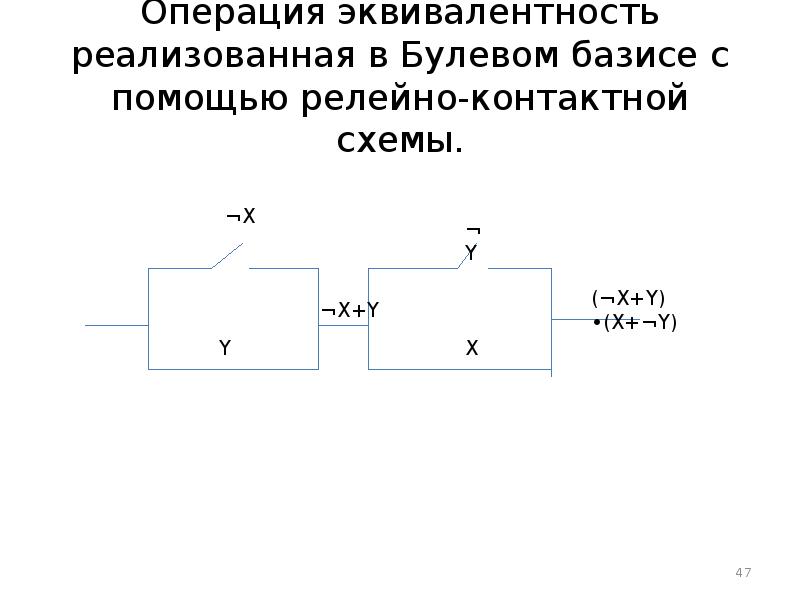
- 47. Операция эквивалентность реализованная в Булевом базисе с помощью релейно-контактной схемы.
- 48. Таблица истинности(переключательная таблица) С помощью таблиц истинности получаем результат логической функции
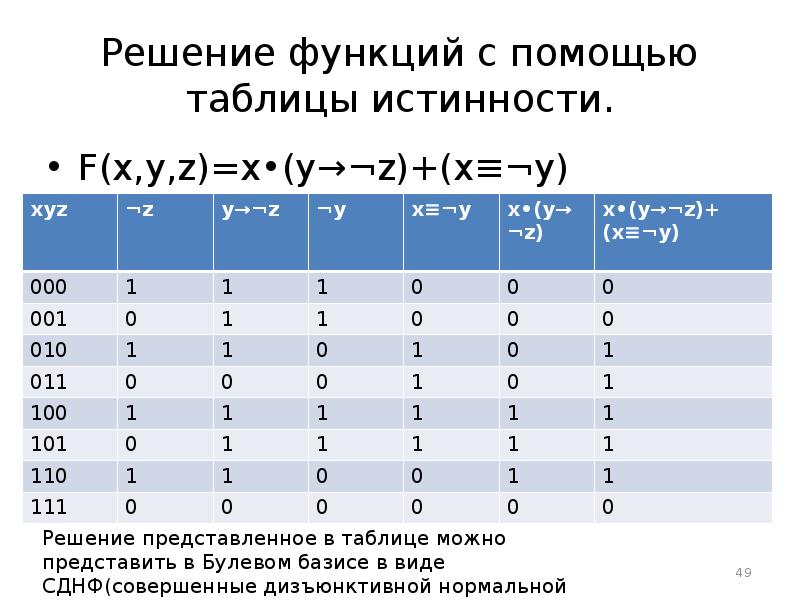
- 49. Решение функций с помощью таблицы истинности. F(x,y,z)=x•(y→¬z)+(x≡¬y)
- 50. Решение функций с помощью таблицы истинности. F(x,y,z)=x•(y→¬z)+(x≡¬y)
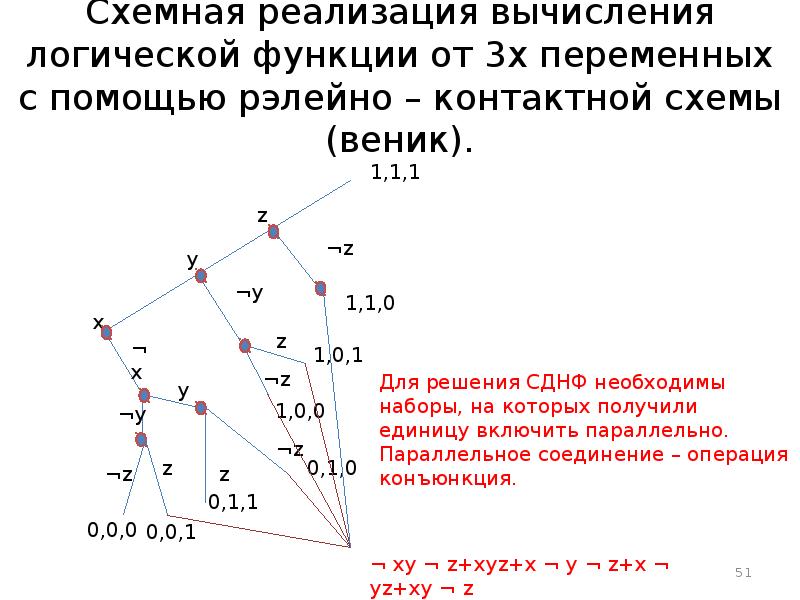
- 51. Схемная реализация вычисления логической функции от 3х переменных с помощью рэлейно
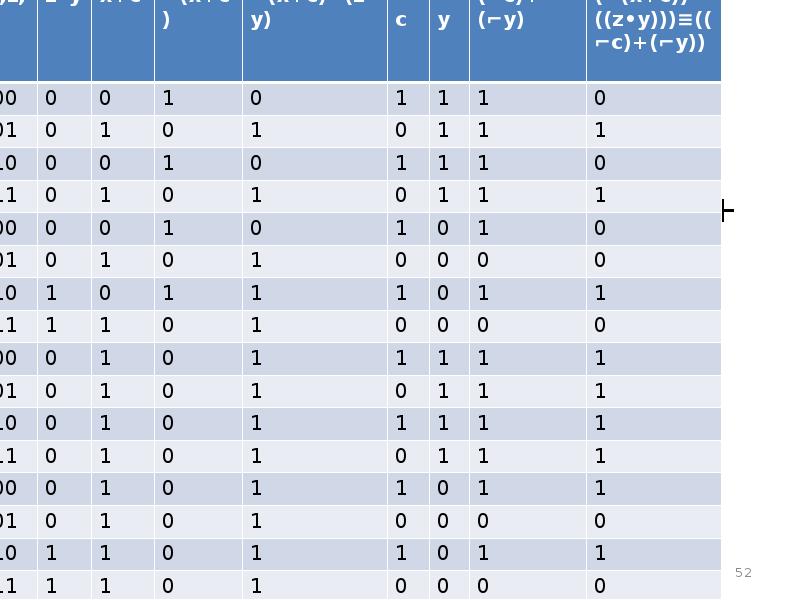
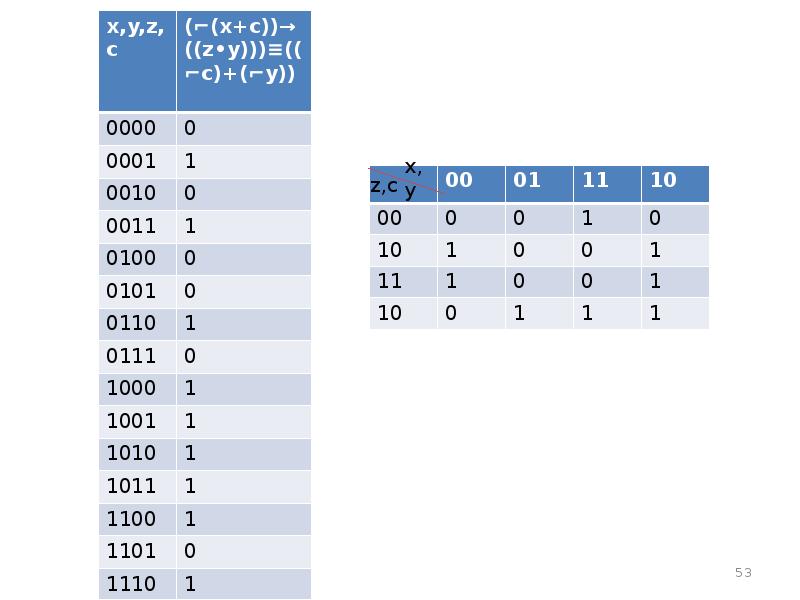
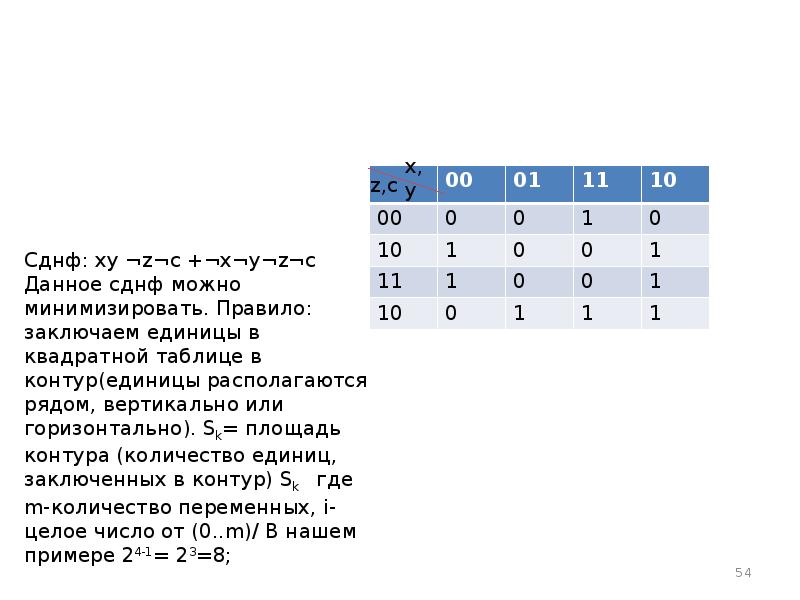
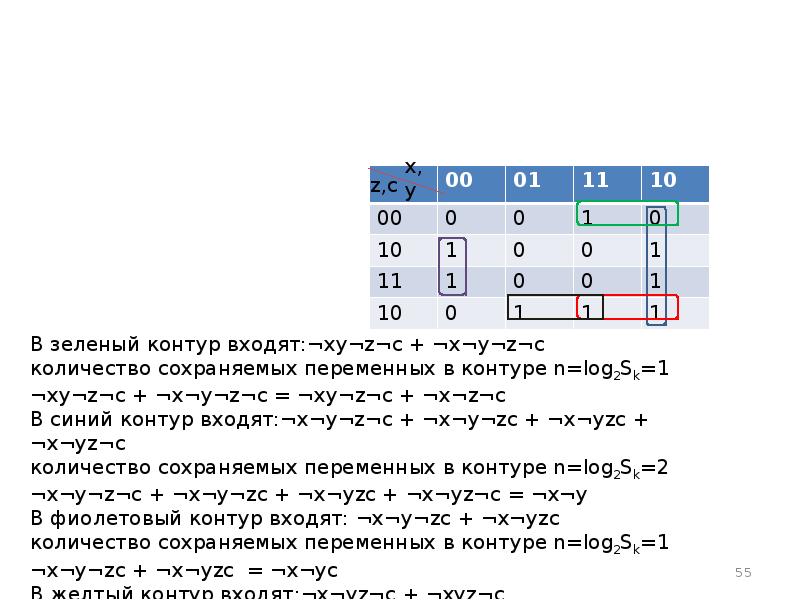
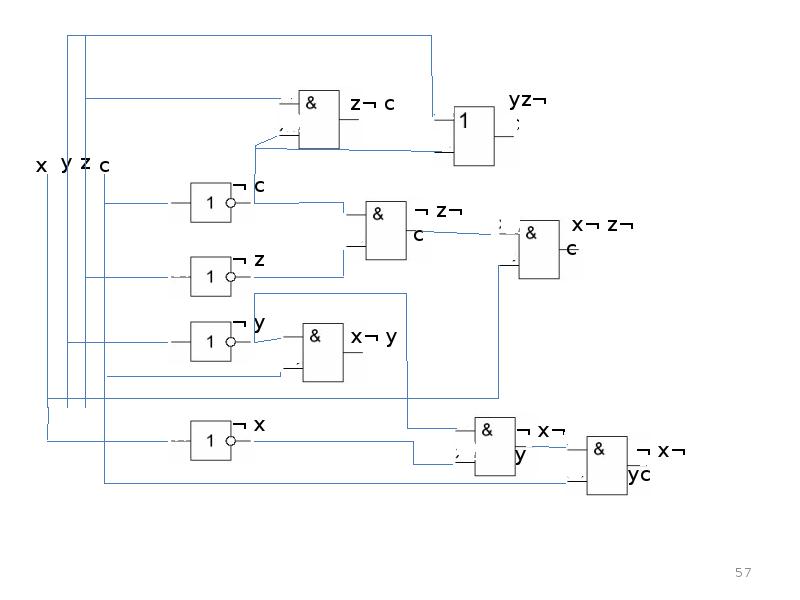
- 52. Минимизация СДНФ с использованием карты Карно. Имеем логическую функцию F(x,y,z,c)=(⌐(x+c))→((z•y)))≡((⌐c)+(⌐y))
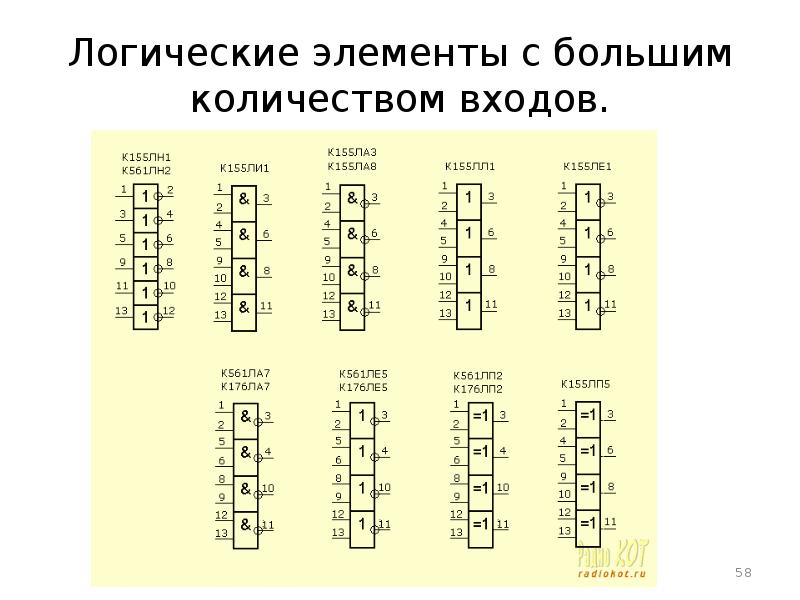
- 58. Логические элементы с большим количеством входов.
- 59. Графы. Граф состоит из множества вершин и множества ребер (ребра соединяют
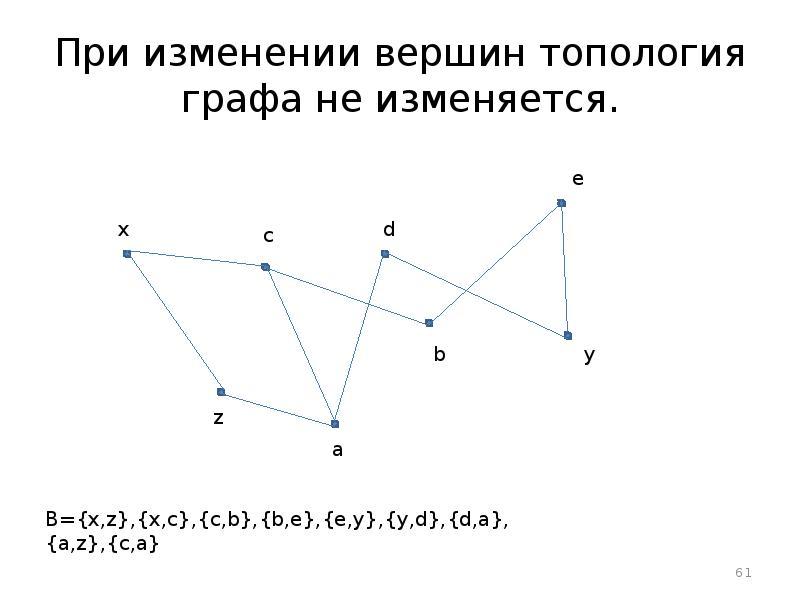
- 60. Неориентированный граф. A={x,y,z,c,a,b,d,e} – множество вершин. B={{x,z},{x,c},{c,b},{b,e},{e,y},{y,d},{d,a},{a,z},{c,a}} – множество ребер.
- 61. При изменении вершин топология графа не изменяется.
- 62. Задание графа с помощью отношения смежности. Отношение смежности отношение между вершинами
- 63. Зададим неориентированный граф через отношение смежности.
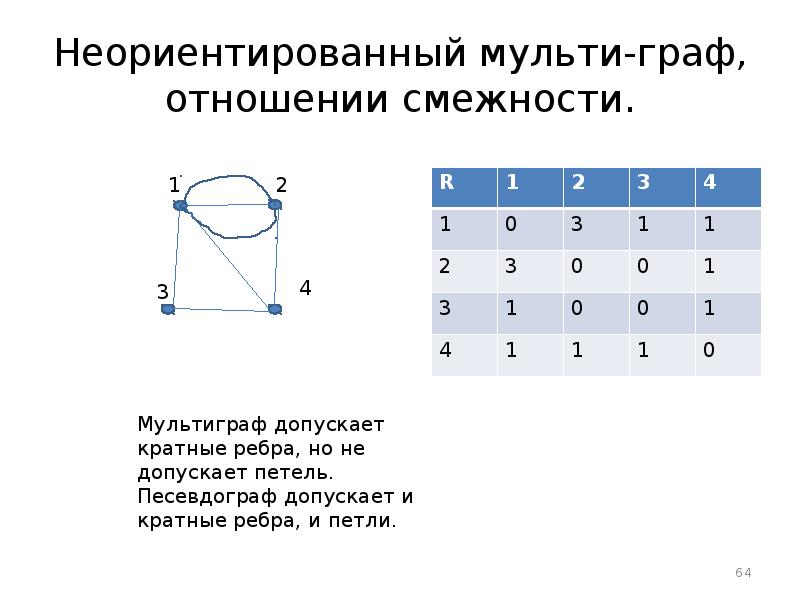
- 64. Неориентированный мульти-граф, отношении смежности.
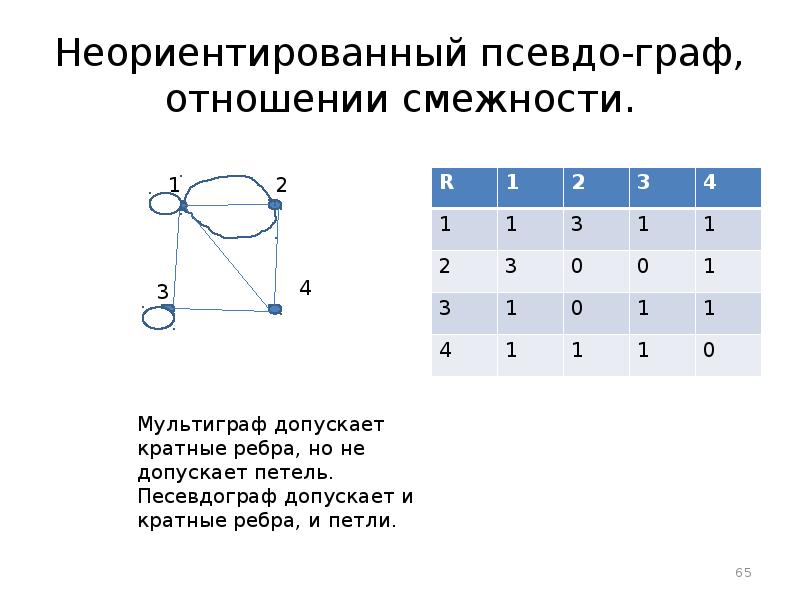
- 65. Неориентированный псевдо-граф, отношении смежности.
- 66. Ориентированный граф. A={x,y,z,c,a,b,d,e} – множество вершин. B={(z,x),(x,c),(c,b),(b,e),(e,y),(y,d),(d,a),(a,z),(c,a)(b,d)} – множество ребер.
- 67. Зададим ориентированный граф через отношение смежности.
- 68. Неориентированный граф. Можем задать через отношение инцидентности. A={x,y,z,c,a,b,d,e} – множество вершин.
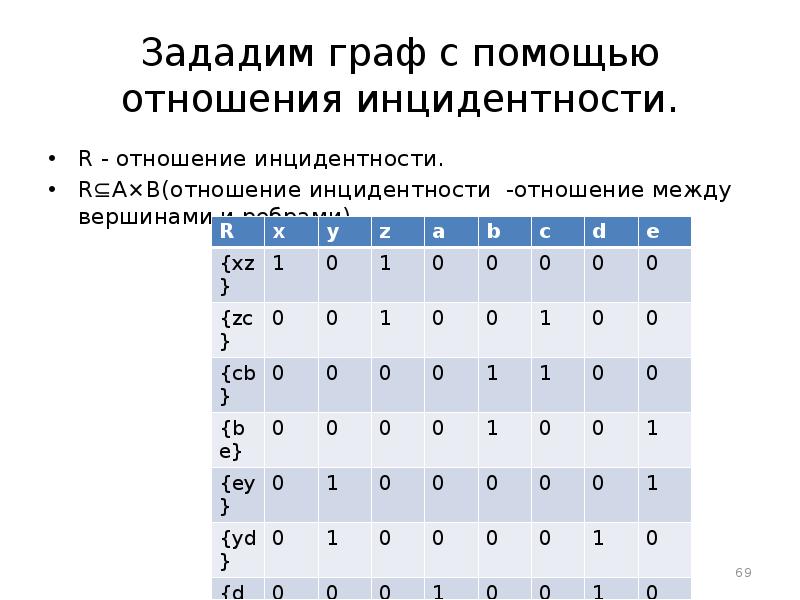
- 69. Зададим граф с помощью отношения инцидентности. R - отношение инцидентности. R⊆A×B(отношение
- 70. Ориентированный граф A={x,y,z,c,a,b,d,e} – множество вершин. B={(z,x),(x,c),(c,b),(b,e),(e,y),(y,d),(d,a),(a,z),(c,a)(b,d)} – множество ребер.
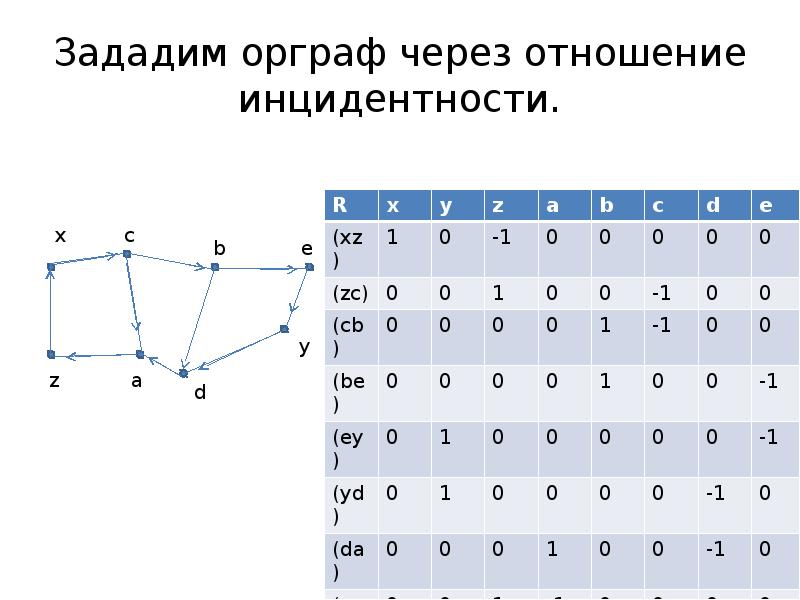
- 71. Зададим орграф через отношение инцидентности.
- 72. Числа характеризующие граф. Степенью вершины называется количество ребер, выходящих из этой вершины.
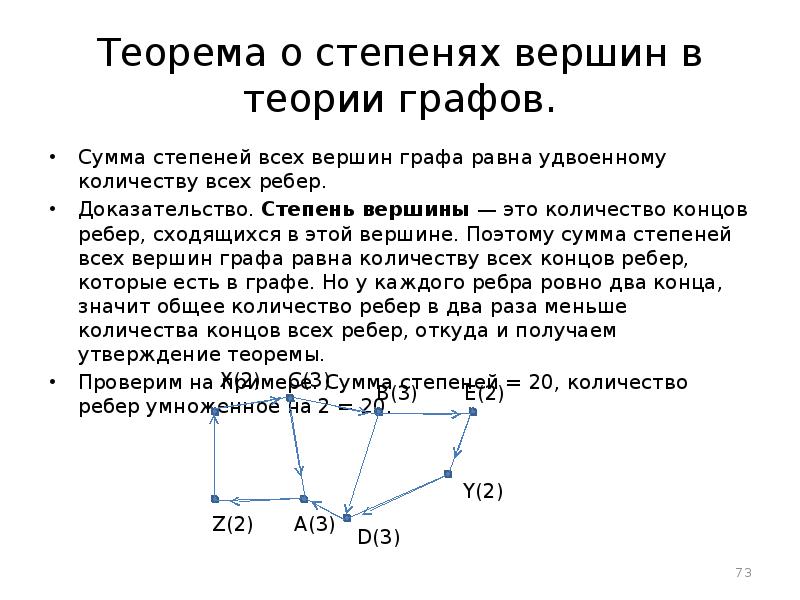
- 73. Теорема о степенях вершин в теории графов. Сумма степеней всех вершин графа равна
- 74. Цикломатическое число. Цикломатическим числом графа - называется число u=N-n+p, где N-
- 75. Найдем путь орг. графа (x,c,b,e,y,d,a,z,x) (x,c,a,z,x) (x,c,b,d,a,z,x)
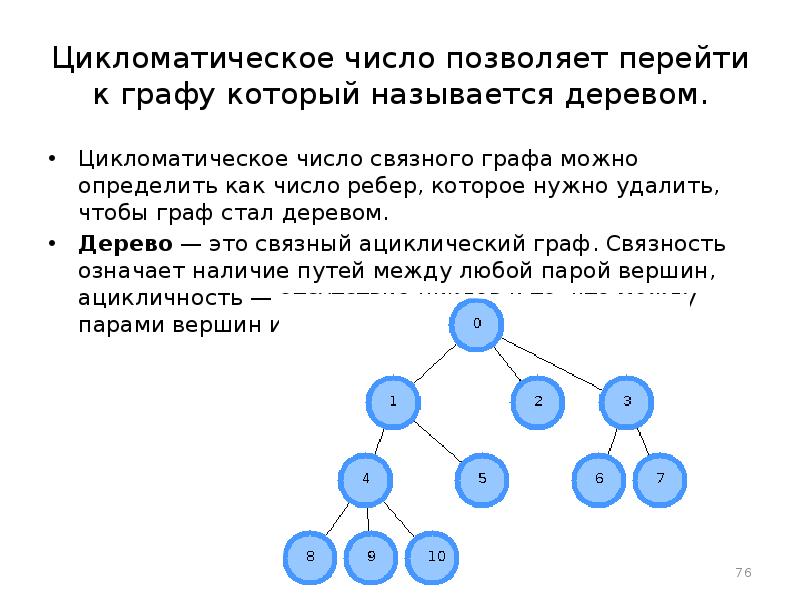
- 76. Цикломатическое число позволяет перейти к графу который называется деревом. Цикломатическое число
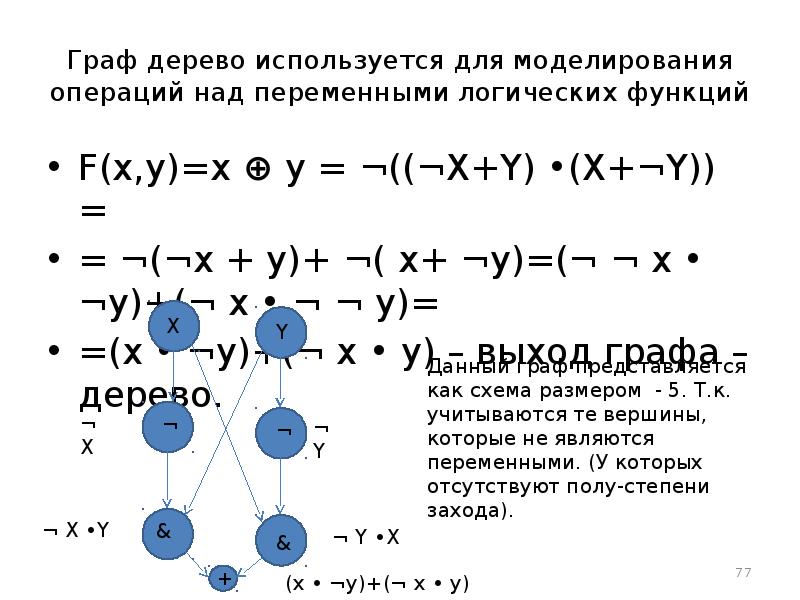
- 77. Граф дерево используется для моделирования операций над переменными логических функций F(x,y)=x
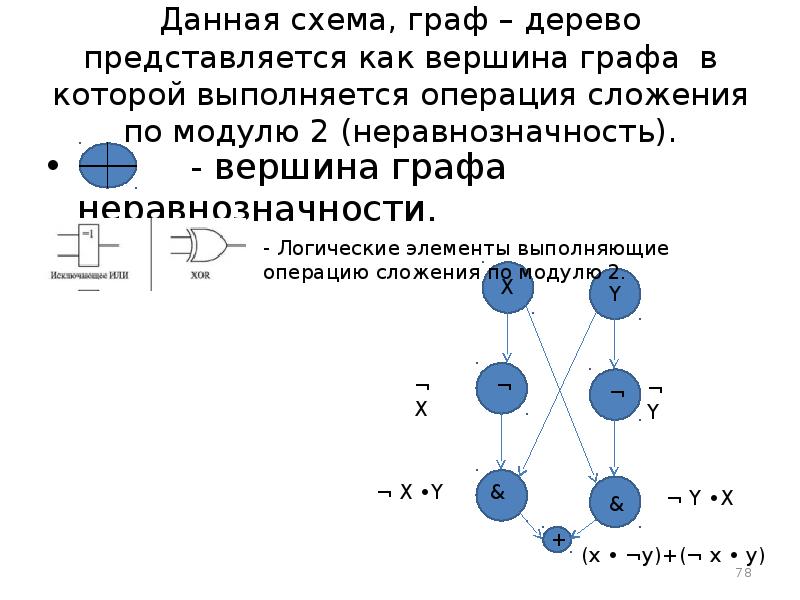
- 78. Данная схема, граф – дерево представляется как вершина графа в которой
- 79. Рассмотрим функцию сложения по модулю 2. f:An→B A – область определения
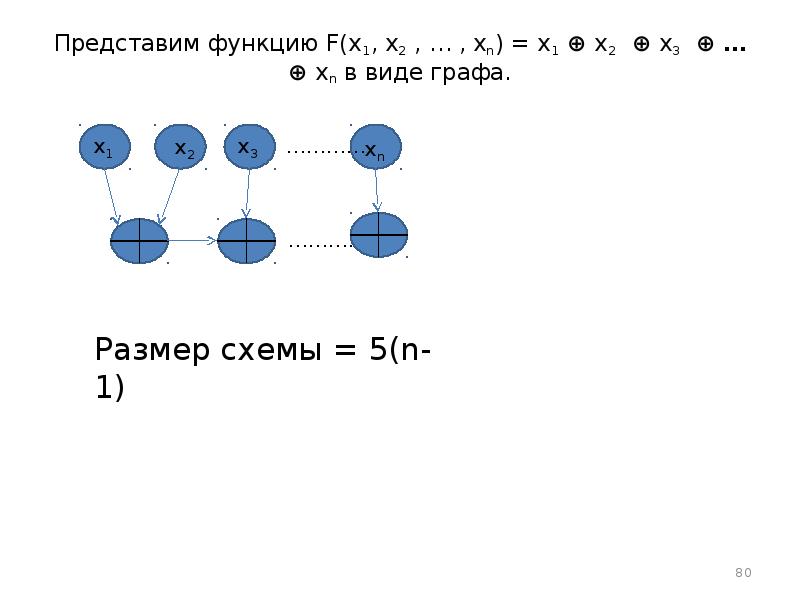
- 80. Представим функцию F(x1, x2 , … , xn) = x1 ⊕
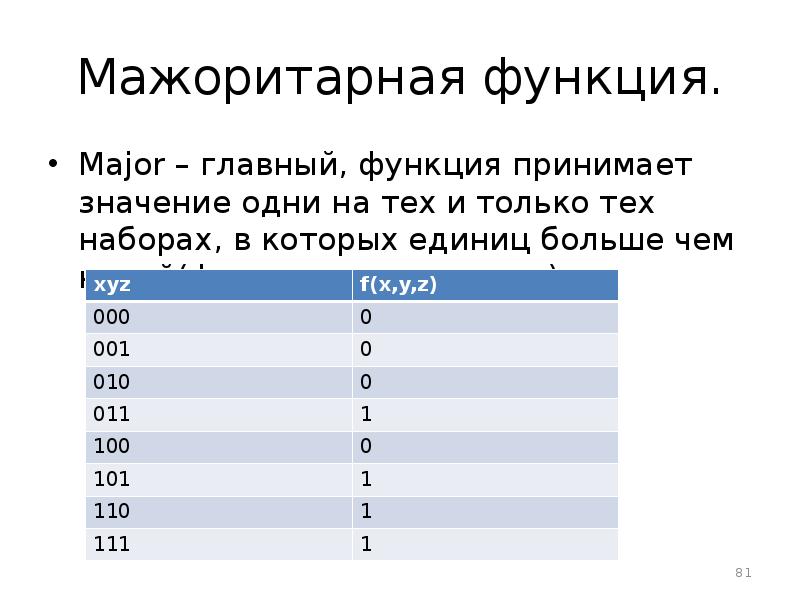
- 81. Мажоритарная функция. Major – главный, функция принимает значение одни на тех
- 82. Скачать презентацию












































Слайды и текст этой презентации
Похожие презентации





























