Формула Стокса. Формула Гаусса-Остроградского. Лекция 3.4 презентация
Содержание
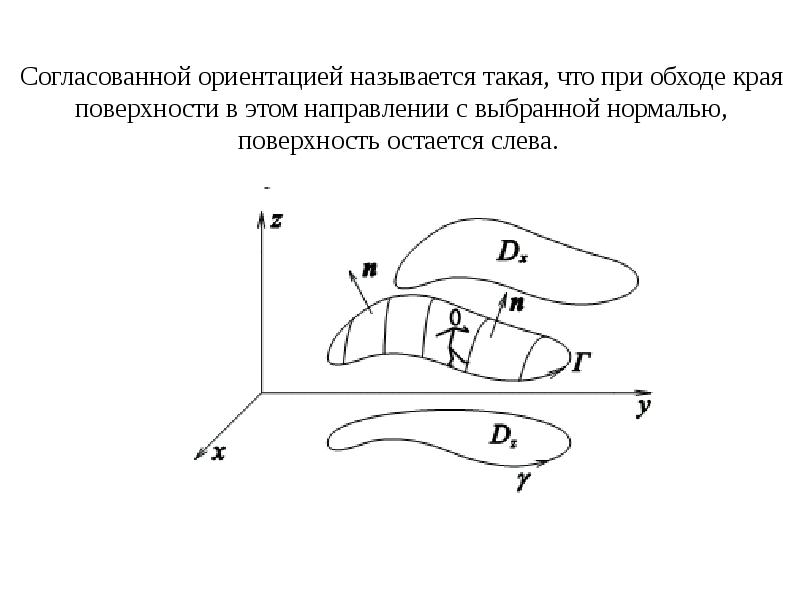
- 2. Согласованной ориентацией называется такая, что при обходе края поверхности в этом
- 3. Пусть задана и непрерывна на Ф и имеет там непрерывные частные
- 4. Ротор поля определяется по формуле
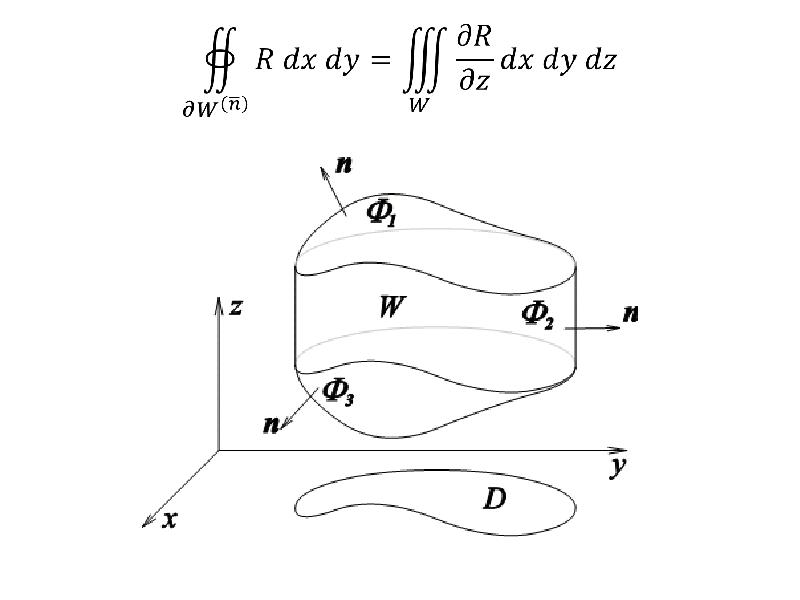
- 5. Теорема (формула Гаусса-Остроградского):
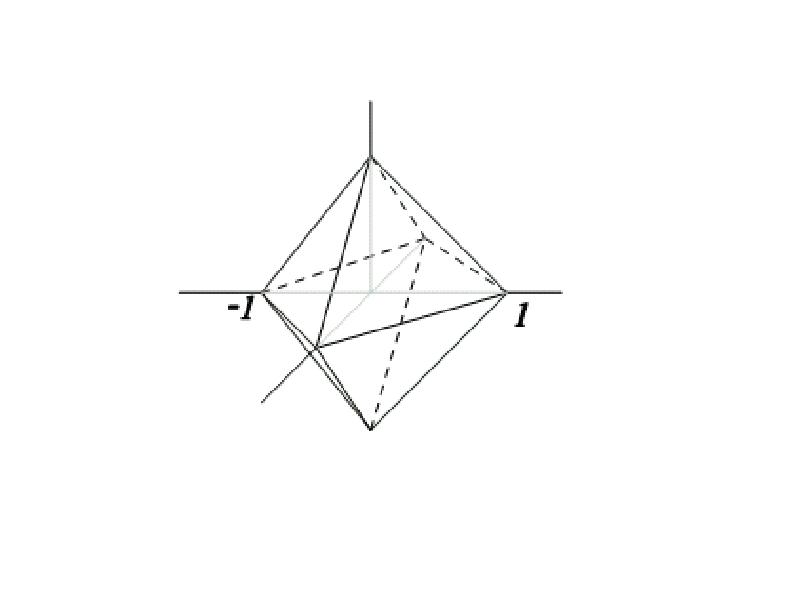
- 7. Пример. Вычислить где Ф :
- 9. Числовые ряды Определение: Возьмём последовательность и построим по ней ещё одну
- 10. Утверждение: Пусть Тогда: Утверждение: Теорема (необходимый признак сходимости ряда):
- 11. Утверждение:
- 12. Теорема (критерий Коши сходимости числового ряда):
- 13. Знакопостоянные ряды Определение: Утверждение:
- 14. Теорема (признак сравнения, признак Вейерштрасса): Следствие (признак сравнения в предельной форме):
- 15. Примеры:
- 16. Скачать презентацию


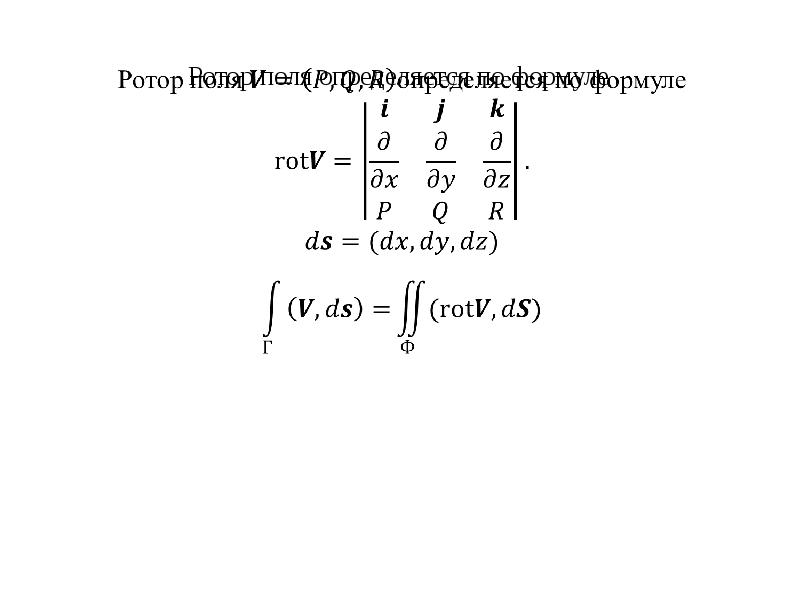









Слайды и текст этой презентации
Скачать презентацию на тему Формула Стокса. Формула Гаусса-Остроградского. Лекция 3.4 можно ниже:
Похожие презентации





























