Интегралы, зависящие от параметра презентация

Лекция 3.13. Интегралы, зависящие от параметра 1. Собственные интегралы, зависящие от параметра Теорема 1. Если f непрерывна на D = {a  x  b, c  y d}, то F(y) непрерывна на [c,d].

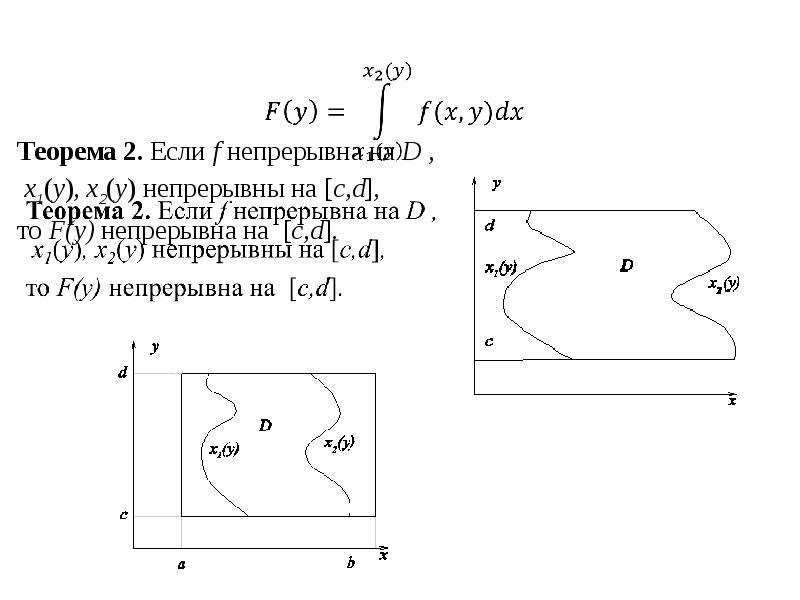
Теорема 2. Если f непрерывна на D , x1(y), x2(y) непрерывны на [c,d], то F(y) непрерывна на [c,d].

Определение. Пусть функция f(x,y) определена на [a,b] для любого yY . Говорят, что f(x,y) равномерно сходится к g(x) на [a,b] при yy0 если  >0 >0x[a,b]yU(y0): |f(x,y) - g(x)|< . Лемма. Если f(x,y) непрерывна и равномерно сходится к g(x) на [a,b] при yy0 , то функция g(x) непрерывна на [a,b]. Теорема 4. Если f(x,y) непрерывна и равномерно сходится к g(x) на [a,b] при yy0 , то

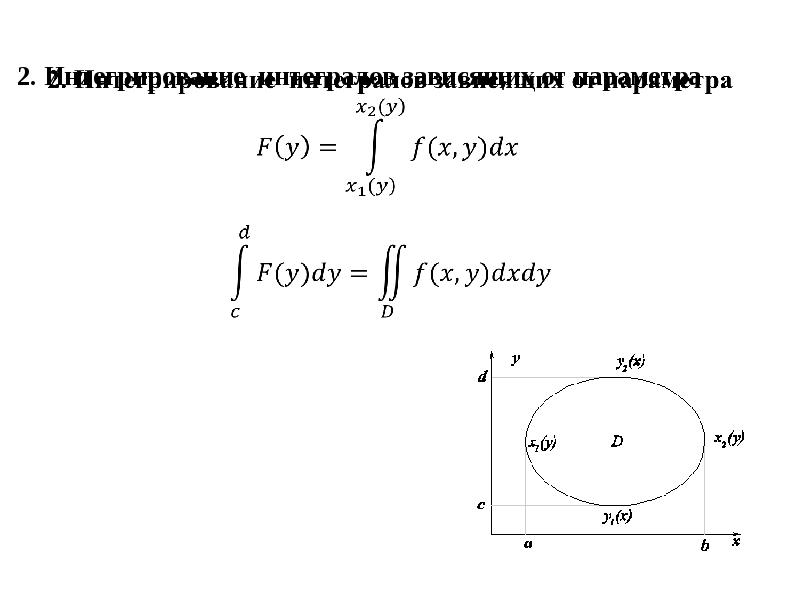
2. Интегрирование  интегралов зависящих от параметра

3. Дифференцирование интегралов, зависящих от параметра Теорема (Лейбниц) 5. Если f и непрерывны в , то дифференцируема на и

Теорема 6. Если f и ее производная непрерывны на имеют непрерывные на производные, то также имеет производную

4. Несобственные интегралы, зависящие от параметра , yY. Определение. Сходящийся на Y интеграл называется равномерно сходящимся на Y, если (для интеграла 1-го рода) (для интеграла 2-го рода)

Теорема (критерий Коши): Пример:

Признак Вейерштрасса равномерной сходимости (для интеграла 2-го рода)(верен и для интегралов 1-го рода) Если на , интегрируемая на любом такая, что то интеграл сходится равномерно на Y.  

Теорема. Пусть определена и непрерывна на по x для всех yY. Если для любых  функция равномерно сходится к на при yy0 , интеграл равномерно сходится на Y, сходится. Тогда