Исследование функций и построение графиков презентация
Содержание
- 2. Теоретический материал
- 3. Содержание 1) Область определения функции 2) Свойства функции (четность, нечетность, периодичность)
- 4. Область определения функции
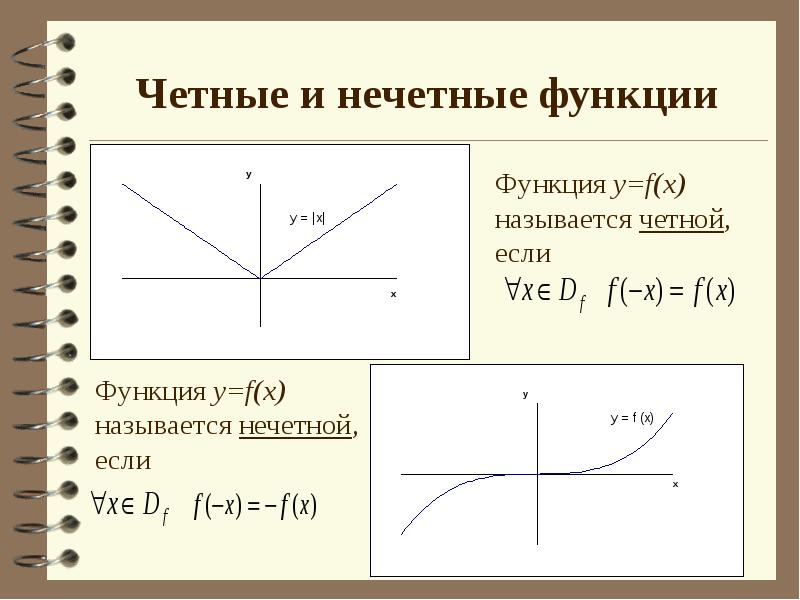
- 5. Четные и нечетные функции
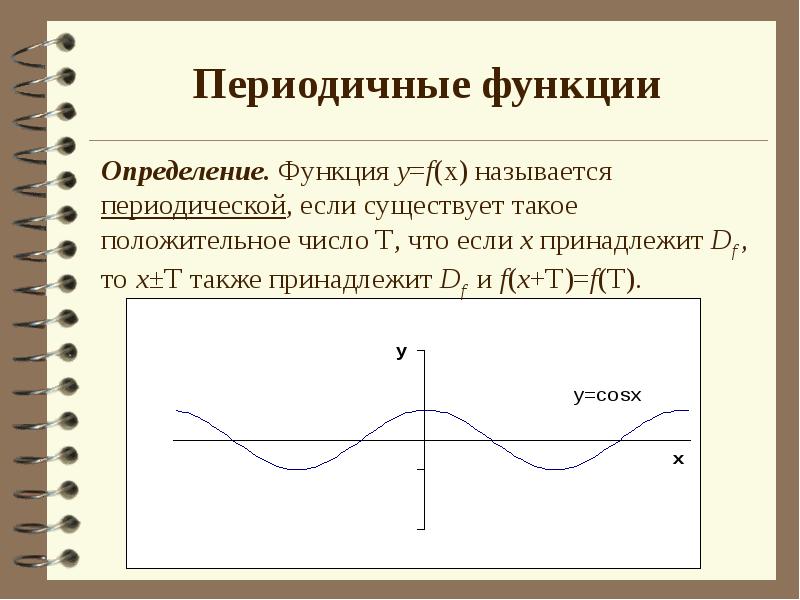
- 6. Периодичные функции
- 7. Точки пересечения с осями координат При исследовании функции необходимо
- 8. Непрерывность Характер точек разрыва Функция у=f(x) называется непрерывной в
- 9. Точки разрыва функции Определение. Точкой разрыва функции называется точка из области
- 10. Классификация точек разрыва Точки устранимого разрыва
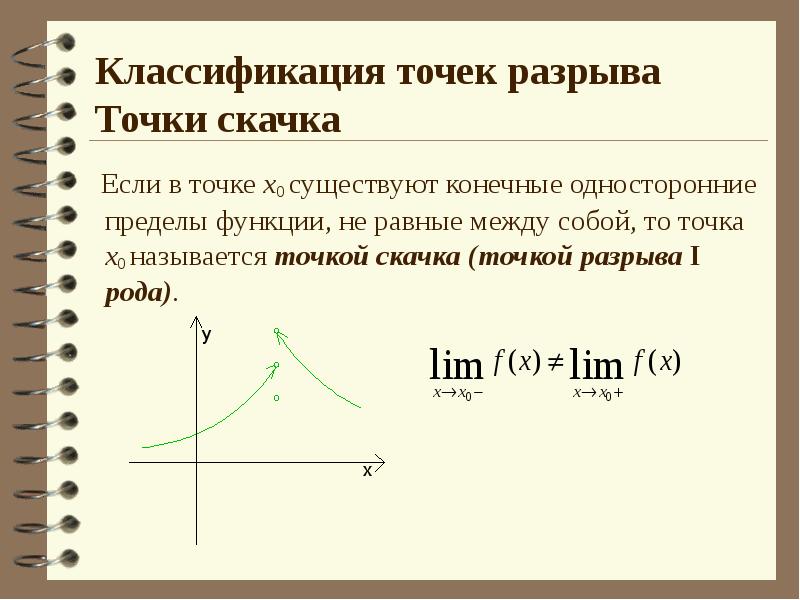
- 11. Классификация точек разрыва Точки скачка Если в точке х0 существуют
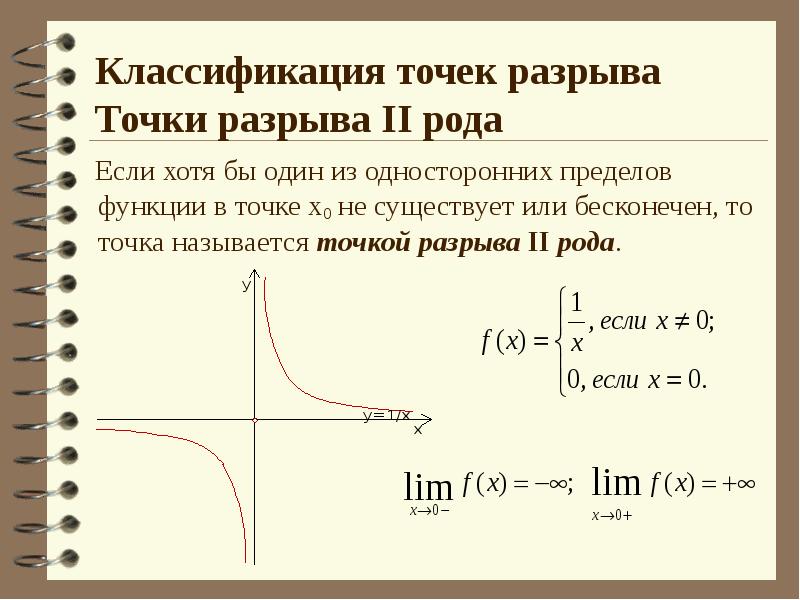
- 12. Классификация точек разрыва Точки разрыва II рода Если хотя бы
- 13. Вертикальные асимптоты
- 14. Наклонные асимптоты Если существует прямая y=kx+b такая, что
- 15. Экстремумы функции Пусть функция f (x) определена и непрерывна
- 16. Исследование функции на монотонность
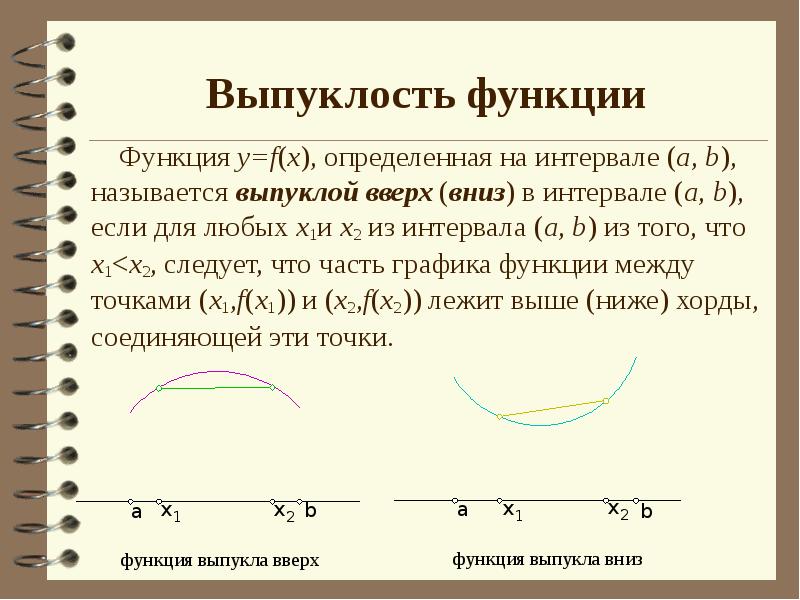
- 17. Выпуклость функции Функция у=f(х), определенная на интервале (а, b),
- 18. Выпуклость функции. Точки перегиба Если график функции в точке
- 19. Достаточные условия выпуклости функции и существования точек перегиба Достаточное условие
- 20. Практический материал
- 21. Исследуем функцию и построим её
- 22. 4). Найдём наклонные асимптоты при в виде
- 23. 5). Найдём точки пересечения с осями координат. Имеем: 5).
- 24. 6) Найдём производную: 6) Найдём производную: Очевидно, что f´(x) ≥
- 25. 7) Найдём вторую производную: 7) Найдём вторую производную: Знаменатель этой
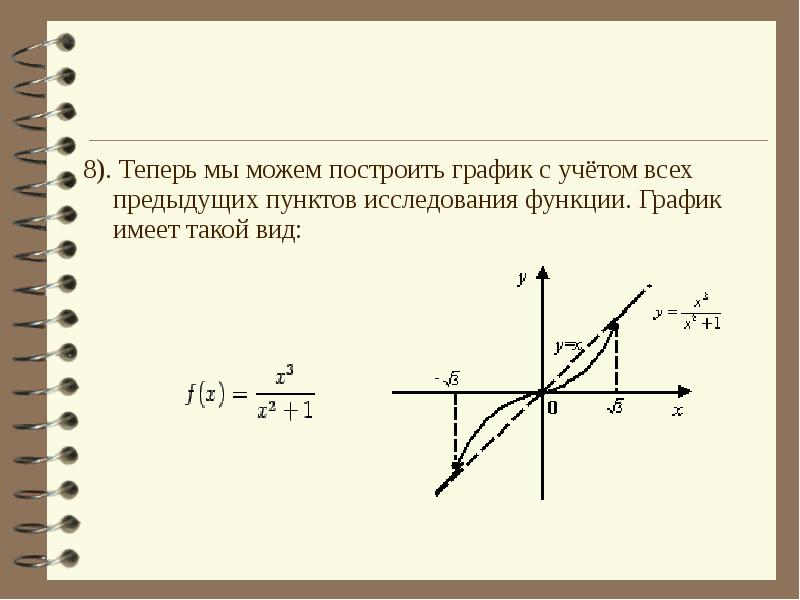
- 26. 8). Теперь мы можем построить график с учётом всех предыдущих пунктов
- 27. Исследуем функцию f(x) = (x2 – 2x)ex и построим её график.
- 28. 4) Будем искать наклонные асимптоты в виде y = kx +
- 29. Теперь найдём значение b по формуле
- 30. Знак функции определяется множителем x2 – 2x, поскольку ex >0 при
- 31. Значение функции в этой точке равно Значение функции в этой точке
- 32. Становится очевидно, что область значений функции -- это 7) По эскизу
- 33. Ясно, что на интервале
- 34. Скачать презентацию



























Слайды и текст этой презентации
Скачать презентацию на тему Исследование функций и построение графиков можно ниже:
Похожие презентации





























