Изучение вопросов измерения геометрических фигур (на примере темы «Площадь многоугольника») презентация

Лекция 10 Изучение вопросов измерения геометрических фигур (на примере темы «Площадь многоугольника»)

Вопросы: Какие геометрические величины вы знаете? Что такое длина? Что такое площадь? Что значит измерить геометрическую величину? Как можно измерить площадь геометрической фигуры?

План: Геометрические величины и идея их измерения в школьном курсе математики Введение понятия «площадь многоугольника» в 8 классе Методические особенности изучения площадей частных видов многоугольников

Основная литература: Федеральный Государственный образовательный стандарт общего образования (Предметная область «Математика», основная школа ‒ WWW.school.edu.ru) и Примерная программа по математике для средней школы (основная школа). Методика и технологии обучения математике. Курс лекций /Под научн. ред. Н.Л.Стефановой и Н.С.Подходовой‒ М.,Дрофа, 2005. лекция 23.3 (изучение частных видов четырехугольников и их площадей)

Основная литература: Атанасян Л.С. и др. Геометрия 7‒9 классы. ‒ М., Просвещение, 1995 и др. годы издания Александров и др. Геометрия 7‒9 классы. ‒ М., Просвещение, 2001 Смирнова И.М., Смирнов В.А. Геометрия 7‒9 классы. ‒ М., Просвещение, 2002 И.Ф.Шарыгин. Геометрия 7‒9 ‒ М., Дрофа, 1999

1. Геометрические величины и идея их измерения в школьном курсе математики Основные сведения Геометрические величины ‒ длина, площадь, объем, мера (градусная или радианная) угла. Каждая из указанных величин задана на определенном множестве геометрических фигур. Например, длина ‒ на множестве отрезков (прямых или кривых); площадь на множестве частей поверхностей (плоских или нет), ограниченных замкнутыми линиями (ломаными или кривыми)

Основные сведения о геометрических величинах (продолжение) Каждая геометрическая величина ‒ аддитивная функция, сопоставляющая ограниченной части пространства (поверхности) единственное число (!) Измерение геометрической величины‒ нахождение ее числового значения через соотнесение с единицей измерения (прямое или косвенное)

Этапы рассмотрения измерения геометрических величин в основной школе В начальной школе ‒ измерение длин и площадей через соотнесение с единицей; разные единицы измерения; способы измерения и формулы для простейших фигур В основной школе вводятся понятия о соответствующих величинах сначала на определенном множестве объектов. Например, длина отрезка прямой, площадь многоугольника Косвенные приемы измерения величин ‒ формулы

В старшей школе Расширяются представления о множестве, на котором рассматриваются геометрические величины и вводятся новые методы их нахождения (площадь и объем ‒ с помощью определенного интеграла) Вывод. Используется индуктивный путь изложения ‒ от практических приемов измерения к теоретическому их обоснованию

2. Введение понятия «площадь многоугольника» в 8 классе (учебник Л.С.Атанасяна) Площадь многоугольника ‒ величина той части плоскости, которую занимает многоугольник Площадь скалярная величина, характеризуется положительным числом Чтобы найти площадь многоугольника нужно узнать, сколько раз единичный квадрат «укладывается» в ограниченной им части плоскости Единичные квадраты ‒ квадратный сантиметр, квадратный метр, квадратный миллиметр

Свойства площади многоугольника Равные многоугольники имеют равные площади Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников Площадь квадрата равна квадрату его стороны

Равносоставленные и равновеликие многоугольники Равносоставленные ‒ те, которые разбиваются на одинаковое число соответственно равных друг другу многоугольников Равновеликие ‒ имеющие равные площади

Если сторона квадрата равна а, то площадь квадрата равна а2. Пусть а = , n N 1 Разделим единичный квадрат на n2 квадратов. S = = =а2

а ‒ конечная десятичная дробь, содержащая n знаков после запятой m = а·10n - целое (натуральное) число Разделим квадрат со стороной а ‒ на m2 равных квадратов сторона маленького кв.

а ‒ бесконечная десятичная дробь обозначим аn ‒ число, полученное из а отбрасыванием десятичных знаков после запятой, начиная с (n+1) ‒го 8,234|17… 8,234 (8,23417…)‒ 8,234 =(0,00017…)≤ 0,001 аn ≤a ≤an+ (аn )2≤a2 ≤(an+ )2 и (аn )2≤S ≤ (an+ )2

3. Методические особенности изучения площадей частных видов многоугольников Последовательность: квадрат →прямоугольник →параллелограмм→треугольник →трапеция

Приемы введения (доказательства) формул для нахождения площадей Квадрат ‒ полная индукция Прямоугольник ‒ достраивание до квадрата со стороной (а + b) (а+b)2 = 2S +a2 + b2 ab = S

Параллелограмм, треугольник, трапеция Достраивают до (разбивают на) ранее рассмотренной фигуры Устанавливают факт равносоставленности данной фигуры и той, до которой достроена Используют свойство о том, что равносоставленные фигуры имеют равные площади (равновелики)

Иллюстрация для параллелограмма

Приемы доказательства площади трапеции

Особенности задачного материала темы «Площади многоугольников» Виды задач: Доказательство равенства площадей двух фигур Вычисление площадей по известным элементам и обратная задача Получение новых фактов о площадях Получение новых фактов, где площадь используется как посредник

Доказательство равенства площадей двух фигур №447 (Атанасян) АВСD ‒параллелограмм М= SС(D) ___________________ SABCD = SAMD

Вычисление площадей по известным элементам и обратная задача № 469 (Атанасян) Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведенная к стороне АВ равна 11 см. Найдите высоту, проведенную к стороне ВС. Ответ: 8 см

Получение новых фактов о площадях №474 (Атанасян) Сравните площади двух треугольников, на которые разделяется треугольник его медианой. №475 (Атанасян) Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющих равные площади.

Получение новых фактов о площадях № 478 (Атанасян) В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырехугольника равна половине произведения диагоналей. № 467 (Атанасян) Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.

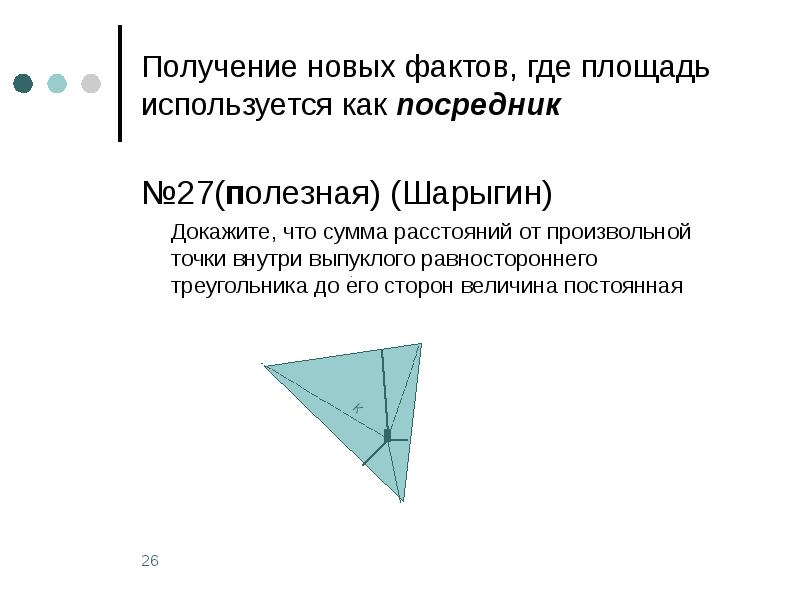
Получение новых фактов, где площадь используется как посредник №27(полезная) (Шарыгин) Докажите, что сумма расстояний от произвольной точки внутри выпуклого равностороннего треугольника до его сторон величина постоянная

Вопросы для самопроверки Правда ли, что площадь геометрической фигуры есть число положительное? Площадь одного многоугольника может быть выражена разными числами (2 см2; 200мм2). Можно ли утверждать, что площадь является функцией? Почему? Показать на чертежах несколько различных приемов обоснования (доказательства) формулы для нахождения площади треугольника