Координаты и векторы презентация

Раздел - 6 Координаты и векторы (20 часов) Прямоугольная декартова система координат в пространстве. Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Разложение вектора по направлениям. Угол между двумя векторами. Проекция вектора на ось. Координаты вектора. Скалярное произведение векторов. Уравнения сферы, плоскости и прямой. Использование координат и векторов при решении математических и прикладных задач.

Тема – 1 Декартовы координаты в пространстве §18, стр.270, стр.122

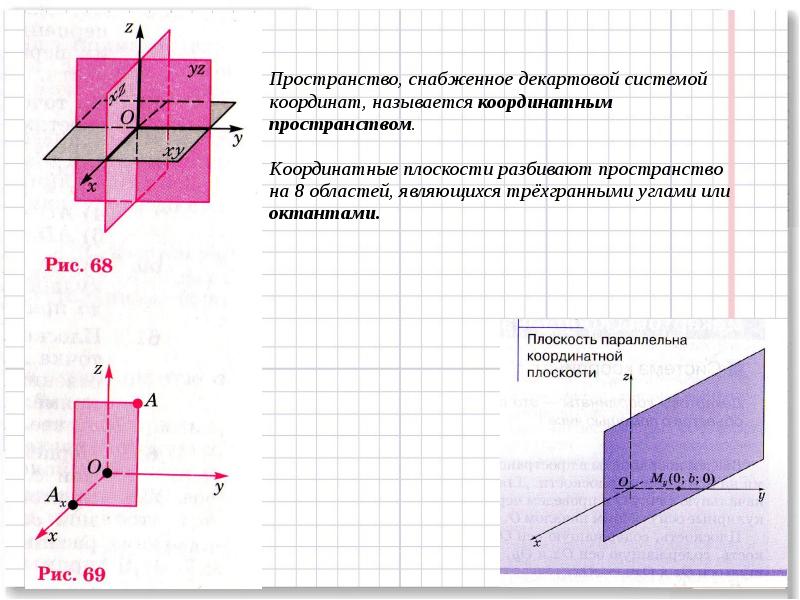
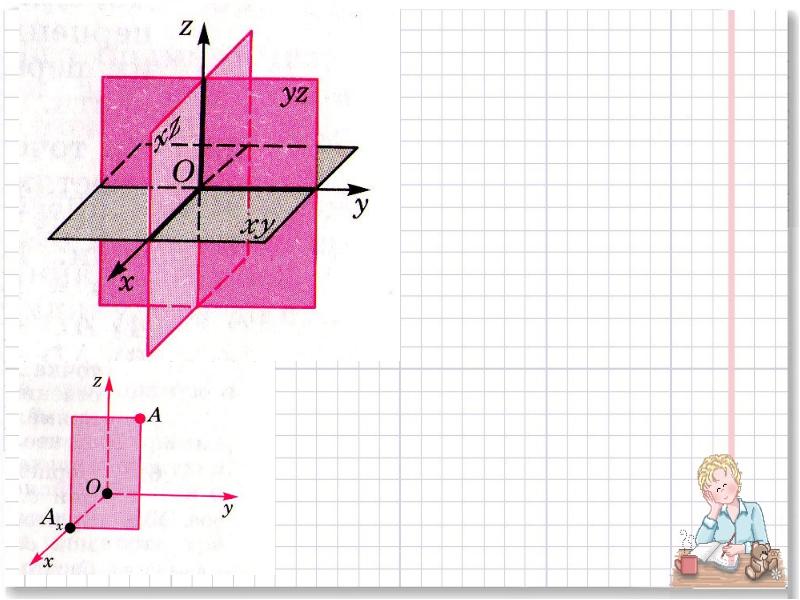
Пространство, снабженное декартовой системой координат, называется координатным пространством. Координатные плоскости разбивают пространство на 8 областей, являющихся трёхгранными углами или октантами.

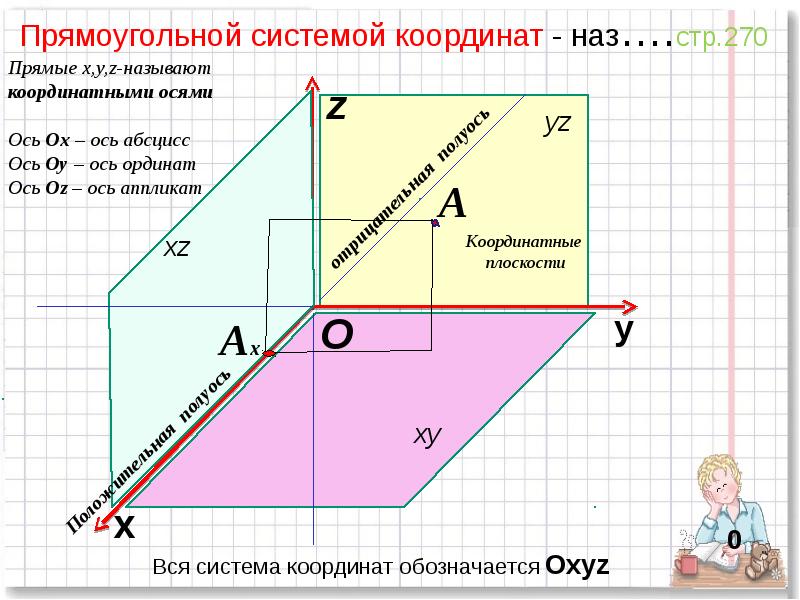
Прямоугольной системой координат - наз….стр.270

Рене Декарт

Задача №2 (стр. 271) Дано: А(1;2;3) В(0;1;2) С (0;0;3) D(1;2;0) Отметить точки А,В,С,D в прямоугольной системе координат.

Расстояние между точками стр. 272 Дано: А (-1;2;3) В(0;1;-2) С (0;0;3) D(4;2;0) Найти: расстояние между точками АВ и СД.

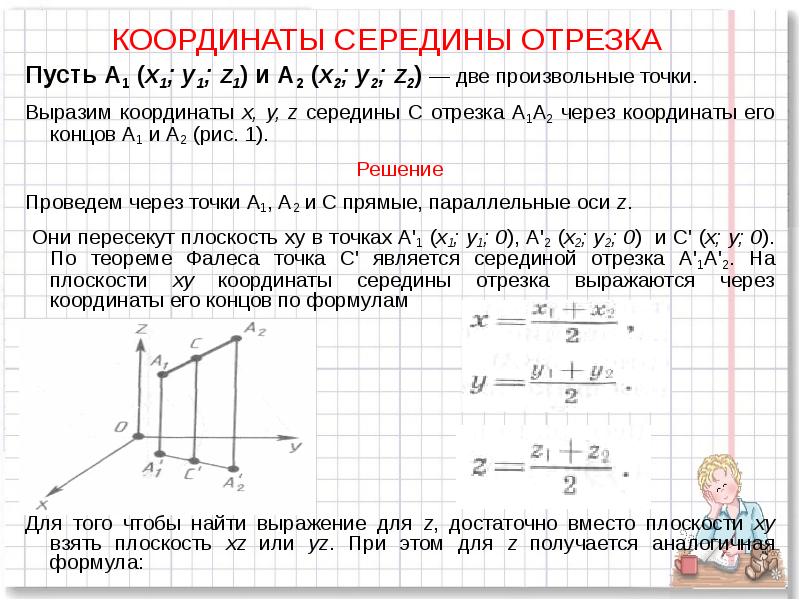
КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА Пусть А1 (x1; y1; z1) и А2 (х2; у2; z2) — две произвольные точки. Выразим координаты х, у, z середины С отрезка А1А2 через координаты его концов А1 и А2 (рис. 1). Решение Проведем через точки А1, А2 и С прямые, параллельные оси z. Они пересекут плоскость ху в точках А'1 (x1; y1; 0), А'2 (х2; у2; 0) и С' (х; у; 0). По теореме Фалеса точка С' является серединой от­резка А'1А'2. На плоскости ху координаты середины отрезка выражаются через координаты его концов по формулам Для того чтобы найти выражение для z, достаточно вместо плоскости ху взять плоскость xz или yz. При этом для z получается аналогичная формула:

Задание-2. 1) Найти длину отрезка А7А8, если А7(6;-4;5), А8(-4;5;-3). 2) Найти координаты середины отрезка А7А8. Решение. Формула длины отрезка: А7А8=√(х2-х1)²+(у2-у1)²+(z2-z1)² А7А8=√

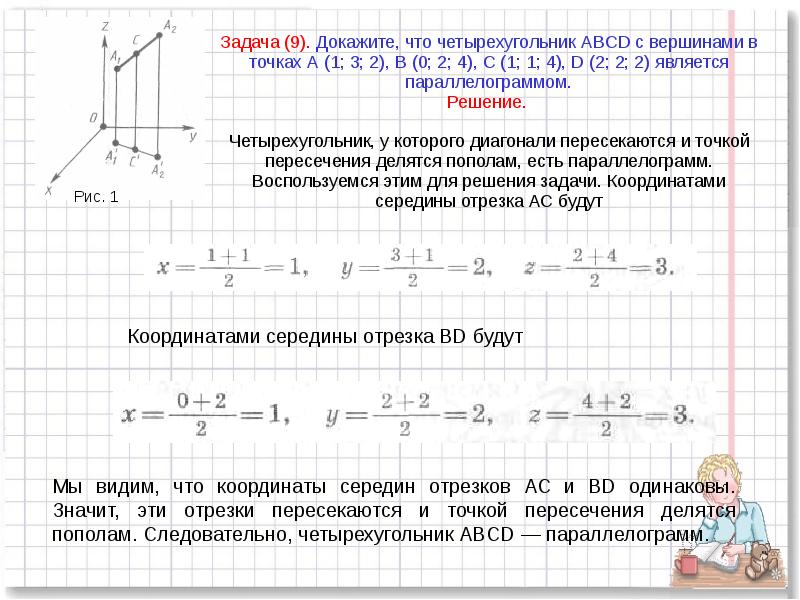
Задача (9). Докажите, что четырехугольник ABCD с вершинами в точках А (1; 3; 2), В (0; 2; 4), С (1; 1; 4), D (2; 2; 2) является параллелограммом. Решение. Четырехугольник, у кото­рого диагонали пересекаются и точкой пересечения делят­ся пополам, есть параллелограмм. Воспользуемся этим для решения задачи. Координатами середины отрезка АС будут

ПРЕОБРАЗОВАНИЕ СИММЕТРИИ В ПРОСТРАНСТВЕ Понятие преобразования для фигур в пространстве определяется так же, как и на плоскости. Так же, как и на плоскости, определяются преобразования симметрии относительно точки и прямой.

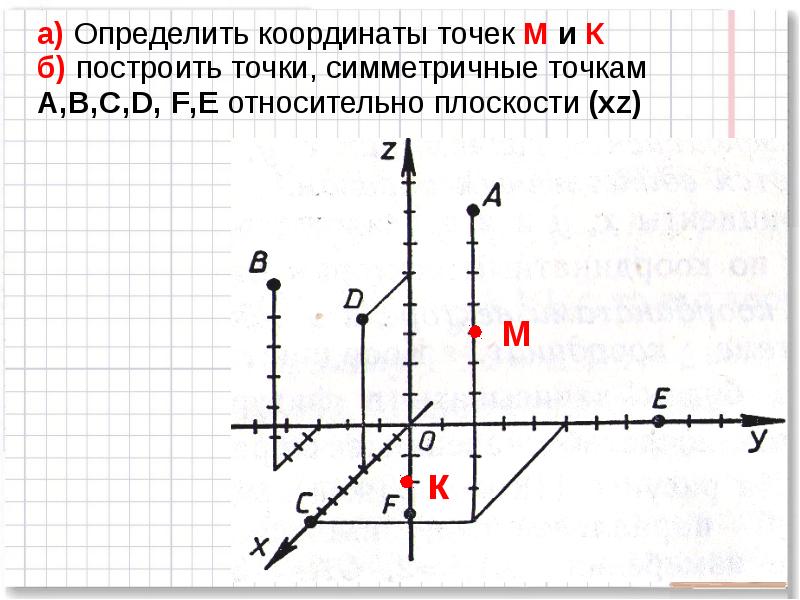
а) Определить координаты точек М и К б) построить точки, симметричные точкам А,В,С,D, F,E относительно плоскости (хz)

Практическая работа по теме: «Прямоугольная декартова система координат в пространстве» Задания. Отметить на модели прямоугольной декартовой с/к в пространстве координаты точки А(х; у; z) Построить на макете с/к точки А1, А2, А3, … А23 (всего их 24), симметричные данной точке А относительно каждой координатной плоскости. 3. Определить в каких плоскостях находятся точки А(… …) и А1(… …), записать их координаты. 4. Найти (по формуле) длину отрезка /АА1/=? и координаты его середины О (х; у; z) - ? Ответ: координаты точки А1 ( …;…;…) длина отрезка /АА1/=… координаты середины О( …;…;…)

Рене Декарт французский философ, математик, физик и физиолог. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввел многие алгебраические обозначения. Декарту принадлежит заслуга создания современных систем обозначений: он ввел знаки переменных величин (x, y, z...), коэффициентов (a, b, c...), обозначение степеней (a2, x-1...). Декарт является одним из авторов теории уравнений: им сформулировано правило знаков для определения числа положительных и отрицательных корней, поставил вопрос о границах действительных корней и выдвинул проблему приводимости, т. е. представления целой рациональной функции с рациональными коэффициентами в виде произведения двух функций этого рода и многое другое..

Домашнее задание Проработать конспект по теме №1 2. С.134-139 (учебник) 3. Найти длину отрезка АВ, если А(-6;3;5), В(-1;5;-2) и координаты его середины