Лекция 7. Булевая алгебра. Элементы математической логики и теории автоматов презентация
Содержание
- 2. 1 Основные понятия алгебры логики Математический аппарат, базирующийся на алгебре логики,
- 3. Значение истинности сложного высказывания зависит от истинности других высказываний, составляющих его.
- 4. Областью определения булевой функции служит совокупность всевозможных n-мерных наборов из единиц
- 5. Число различных функций алгебры логики, зависящих от n аргументов, конечно и
- 6. Число всех функций алгебры логики Аn, существенно зависящих от n аргументов,
- 7. 2 Элементарные булевы функции
- 13. 3 Полнота системы булевых функций Одно из основных понятий алгебры логики
- 14. 4 Законы и тождества алгебры логики
- 15. 4) Дистрибутивности конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции 4) Дистрибутивности
- 16. 8) Поглощения 8) Поглощения x1\/ x1x2 = x1, x1(x1\/x2) = x1
- 17. Правило 2. Если логическое произведение двоичных переменных содержит хотя бы одну
- 18. 5 Представление булевых функций дизъюнктивными и конъюнктивными нормальными формами Любая логическая
- 19. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций: Дизъюнктивной нормальной формой
- 20. Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций: Конъюнктивной нормальной формой
- 22. Пример 1. Привести функцию к СДНФ. Пример 1. Привести функцию к
- 23. Если логическая функция задана таблицей истинности, то построение СДНФ осуществляется по
- 24. Пример 2. Построить СДНФ для функции, заданной таблично. Пример 2.
- 25. Совершенной КНФ (СКНФ) логической функции f от n различных переменных называется
- 26. Пример 3. Построить СКНФ для функции f(x1, x2, x3), заданной таблично.
- 27. 6. Синтез комбинационных схем
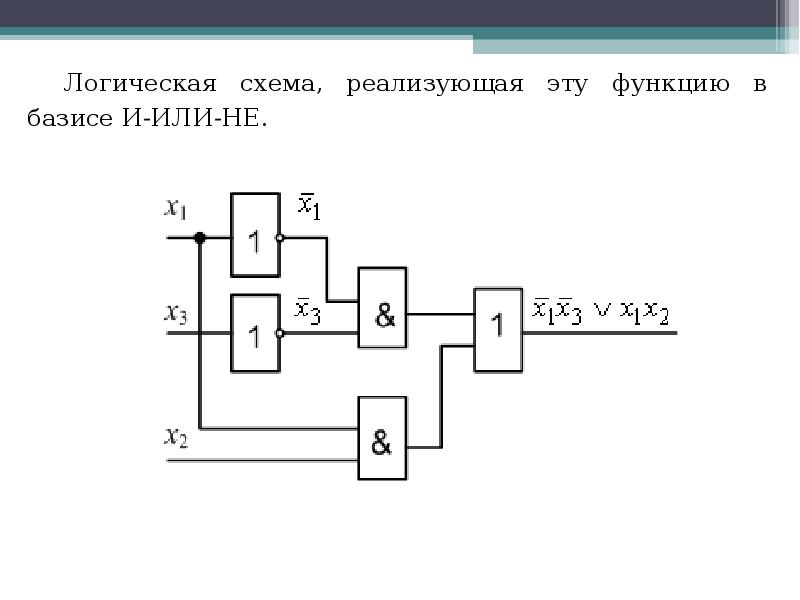
- 30. Логическая схема, реализующая эту функцию в базисе И-ИЛИ-НЕ. Логическая схема, реализующая
- 31. Преобразуем f(x1, x2, x3) к базису И-НЕ: Преобразуем f(x1, x2, x3)
- 32. Преобразуем f (x1, x2, x3) к базису ИЛИ-НЕ: Преобразуем f (x1, x2, x3)
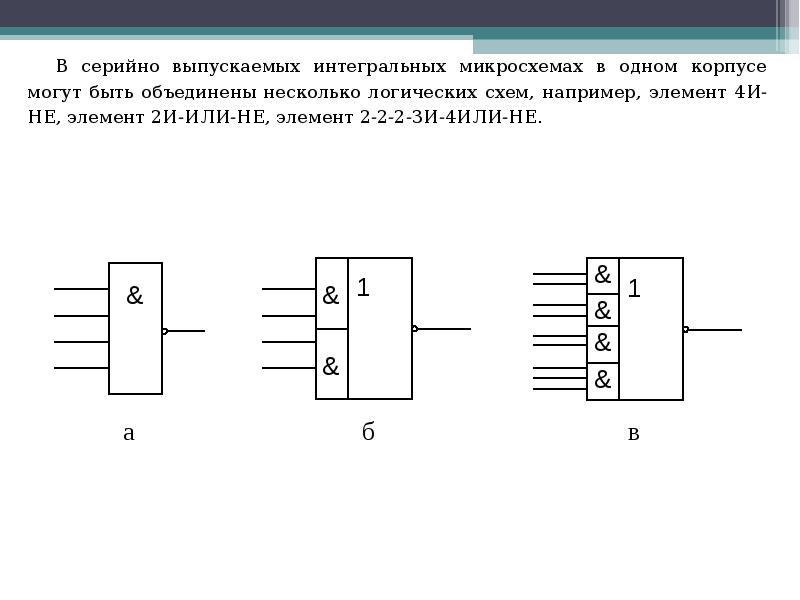
- 33. В серийно выпускаемых интегральных микросхемах в одном корпусе могут быть объединены
- 34. Скачать презентацию































Слайды и текст этой презентации
Скачать презентацию на тему Лекция 7. Булевая алгебра. Элементы математической логики и теории автоматов можно ниже:
Похожие презентации