Математическое моделирование в биологии и медицине презентация

Математическое моделирование в биологии и медицине Авторы Тишков Артем Валерьевич Король Алина Владимировна 2017

Модель Вольтерра (хищник-жертва) Допустим, в некотором замкнутом районе живут зайцы (N1), питающиеся бесконечным количеством растительной пищи, и рыси (N1), питающиеся зайцами. Запишем дифференциальные уравнения, описывающие процесс изменения числа особей во времени. При отсутствии рысей, изменение числа зайцев: dN1=αN1dt α - коэффициент, характеризующий размножение зайцев (жертв). При отсутствии зайцев, изменение числа рысей: dN2=-βN2dt β - коэффициент, характеризующий вымирание рысей (хищников).

Модель Вольтерра (хищник-жертва) При совместном существовании зайцев и рысей: ε - коэффициент, характеризующий убыль зайцев, вследствие их встреч с рысями. γ - коэффициент, характеризующий прирост рысей, вследствие их встреч с зайцами.

Скорость изменения популяций

Стационарное состояние При неизменяющейся численности зайцев и рысей (N1= const и N2= const) N’1= N’2 =0, т.е:

Решение уравнений стационарного состояния

Устойчивость в стационарных состояниях n1 и n2 – случайные отклонения и флуктуации Производные (с учетом того, что то производная от стационарного состояния равна 0)

Устойчивость в стационарных состояниях Подставим производные в уравнения скорости изменения популяций

Устойчивость в стационарных состояниях Подставим производные в уравнения скорости изменения популяций

Устойчивость в стационарных состояниях Раскроем скобки, приведем подобные члены и пренебрежем членами εn1n2 и γn1n2 вследствие их предполагаемой малости. В результате преобразования получим:

Устойчивость в стационарных состояниях Найдем вторую производную:

Устойчивость в стационарных состояниях Окончательно получаем систему линейных дифференциальных уравнений второго порядка, описывающих консервативную колебательную систему, (т.е. идеализированную систему, в которой запас энергии в процессе колебаний остается постоянным):

Решение системы дифференциальных уравнений Напишем характеристическое уравнение: Зададим начальные условия: Тогда:

Решение системы дифференциальных уравнений Выражаем функцию n2 через n1:

Решение системы дифференциальных уравнений

Решение системы дифференциальных уравнений - период колебаний - частота колебаний - круговая частота

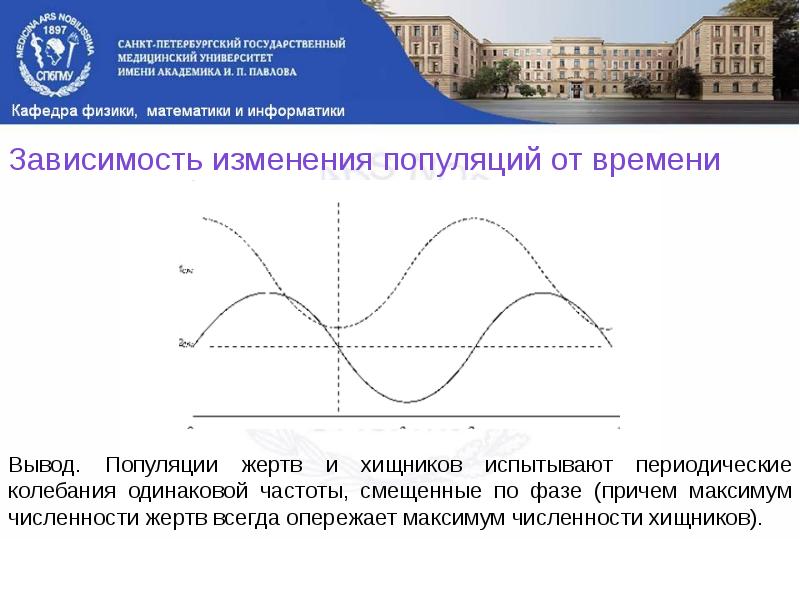
Зависимость изменения популяций от времени

Фазовый портрет системы Рассмотрим график зависимости N1 от N2, т.е. избавимся от t.

Фазовый портрет системы Произведя несложные математические преобразования, мы получили уравнение эллипса, с координатами центра (N1ст,N2ст). При n01=n02=n уравнение эллипса превращается в уравнение окружности с радиусом n.

Решение дифференциальных уравнений Упрощенное решение системы дифференциальных уравнений привело к тому, что модель пришлось слишком идеализировать, что плохо соответствует реальной модели. Сделаем попытку решить систему дифференциальных уравнений другим методом. Разделим одно уравнение на другое, тогда получим или, перемножив, получим выражение

Решение дифференциальных уравнений Разделим переменные, поделив правую и левую части уравнения на  N1N2: Проинтегрируем:

Решение дифференциальных уравнений Преобразуем полученное выражение: или Мы получили выражение, связывающее две переменные N1 и N2, т.е. зависимость N1=f(N1) в неявном виде

Графическая зависимость изменения численности популяций

Графическая зависимость изменения численности популяций Однако и здесь имеют место следующие закономерности: 1.Колебания численности популяций N1 и N2 , действительно имеют место. 2.Частоты этих колебаний весьма близки. 3.Сдвиг по фазе, хотя и не равен π/2 , однако он явно наблюдается.

Фармакокинетическая модель Рассмотрим модель, описывающую кинематику распределения введенных в организм препаратов (лекарств). Будем считать, что терапевтический эффект зависит от концентрации препарата в больном органе (органе-мишени) и времени нахождения лекарства в действующей концентрации. Модель должна дать ответ о дозе лекарства, пути и периодичности введения, которое обеспечивало бы достаточный терапевтический эффект при минимальном побочном действии.

Фармакокинетическая модель Из физиологии известно, что концентрация препарата в органе может зависеть от ряда процессов, скорости которых характеризуются константами К: 1) Всасывание препарата в кровяное русло при внесосудистом введении – константа – К12. 2) Транспорт препарата из крови в органы – К23. 3) Транспорт препарата из органа в кровь – К32.

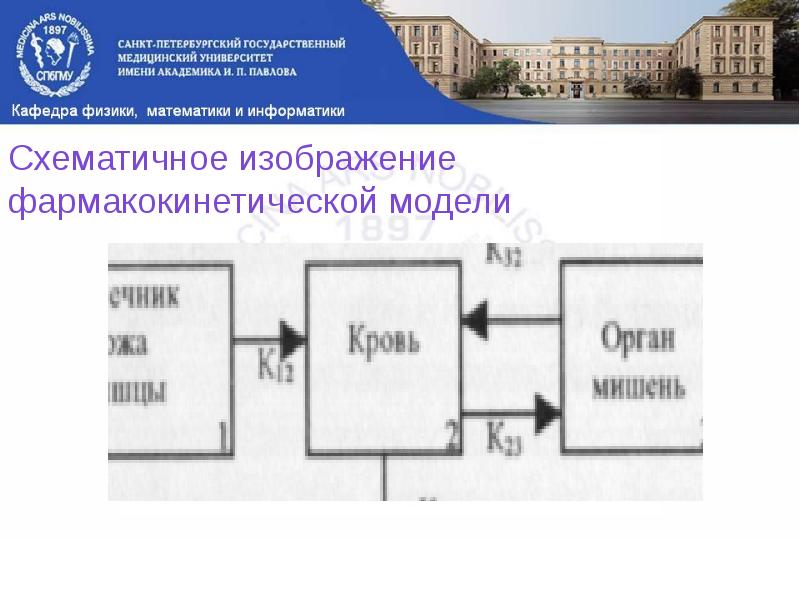
Схематичное изображение фармакокинетической модели

Уравнения изменения скоростей концентраций Всегда решаются, т.е. интегрируются, только дифференциальные уравнения первой степени, к которым и стараются свести путем преобразований и упрощений системы из нескольких уравнений.

Упрощение системы Допустим, что препарат непрерывно со скоростью Q поступает в кровь, тогда изменение его количества в крови: где k – константа удаления препарата из крови

Дифференциальное уравнение и его частное решение Предположим, что в момент t=0, масса препарата в крови m=0.

Зависимость концентрации препарата от времени Для получения зависимости C(t) разделим обе части уравнения на объем V, в котором распределяется препарат. При

Скорость введения препарата Для достижения в крови некоторой постоянной концентрации препарата С* его следует вводить со скоростью Q= С*Vk Время достижения уровня С* будет также будет зависеть от константы скорости выведения препарата k. Таким образом, лечебная концентрация препарата в крови устанавливается не мгновенно, как хотелось бы в лечебных целях, а по прошествии некоторого времени.

Нагрузочная доза препарата Для более быстрого достижения уровня С* сочетать непрерывное введение препарата с начальным разовым введением некоторой нагрузочной дозы mn. Нагрузочная доза препарата в крови будет уменьшаться по закону , из которого следует закон изменения количества препарата со временем:

Уравнения изменения концентрации или Из последнего уравнения видно, что конечный уровень концентрации препарата, т.е. при    по-прежнему равен С* и не зависит от нагрузочной дозы.

Нагрузочная доза препарата Скорость достижения уровня С* зависит от величины   , т.е. нагрузочная доза для мгновенного достижения уровня С* может быть получена из равенства    . Она равна Таким образом для мгновенного создания в крови желаемой концентрации С* необходимо ввести нагрузочную дозу m* и вести инфузию со скоростью Q=C*Vk.

Выводы Этот теоретический вывод был подтвержден экспериментально, что и является решающей проверкой правильности модели. Более сложные модели можно построить путем суммирования блоков, если мы будем оставаться в рамках линейного приближения, т.е. описывать ситуацию линейными дифференциальными уравнениями.