Наука статистика презентация
Содержание
- 2. ВВЕДЕНИЕ Статистика изучает общественные явления с точки зрения двух категорий: КОЛИЧЕСТВО
- 3. ПОКАЗАТЕЛИ СОВОКУПНОСТЬ – это количественное проявление одушевленных или неодушевленных объектов в
- 4. ЗАДАЧА Обследованию подвергнуты рабочие цеха на предмет выявления ТАРИФНОГО РАЗРЯДА, ВОЗРАСТА,
- 5. ТЕОРЕТИЧЕСКАЯ ПОДГОТОВКА 1. Из массива данных выделить совокупности. Это совокупности:
- 6. ТЕОРЕТИЧЕСКАЯ ПОДГОТОВКА 3. Определить варианты по рядам распределения. Статистические распределения могут
- 7. ТЕОРЕТИЧЕСКАЯ ПОДГОТОВКА 4. Определить необходимое число групп (n) Ключевым вопросом статистического
- 8. ИСХОДНЫЕ ДАННЫЕ Варианты тарифного разряда (х) : 4 3 3 6
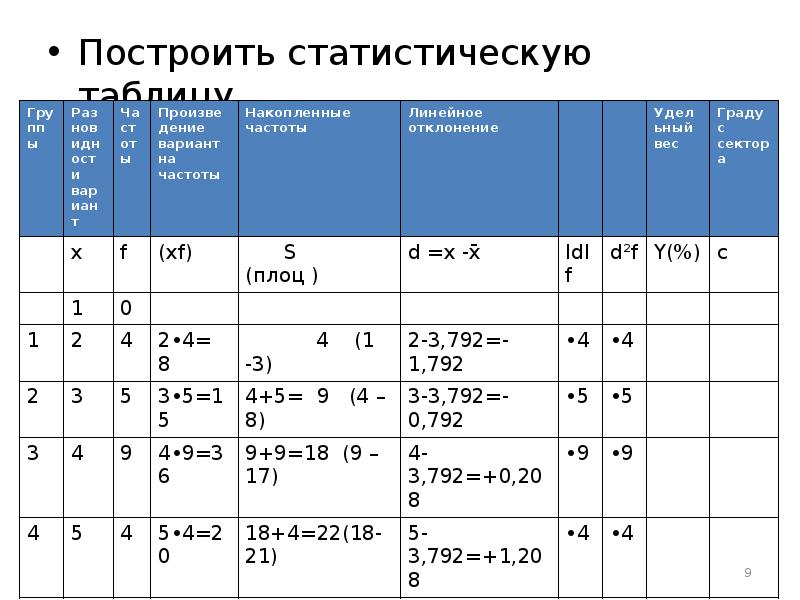
- 9. Построить статистическую таблицу. Построить статистическую таблицу.
- 10. РЕШЕНИЕ 1. Построить дискретный ряд распределения в котором определить: Необходимое число
- 11. РЕШЕНИЕ Дискретный ряд распределяется по пяти группам, поэтому в таблицу заносим
- 12. РЕШЕНИЕ Третья группа – 4 4 4 4 4 4 4
- 13. РЕШЕНИЕ Накопленная частота подсчитывается следующим образом: В первой группе накопленная частота
- 14. РЕШЕНИЕ Распределение по правилу (ПЛОЦ) осуществляется следующим образом: Первая группа (1
- 15. РЕШЕНИЕ Вторая группа (4 – 8). Третья группа (9 – 17).
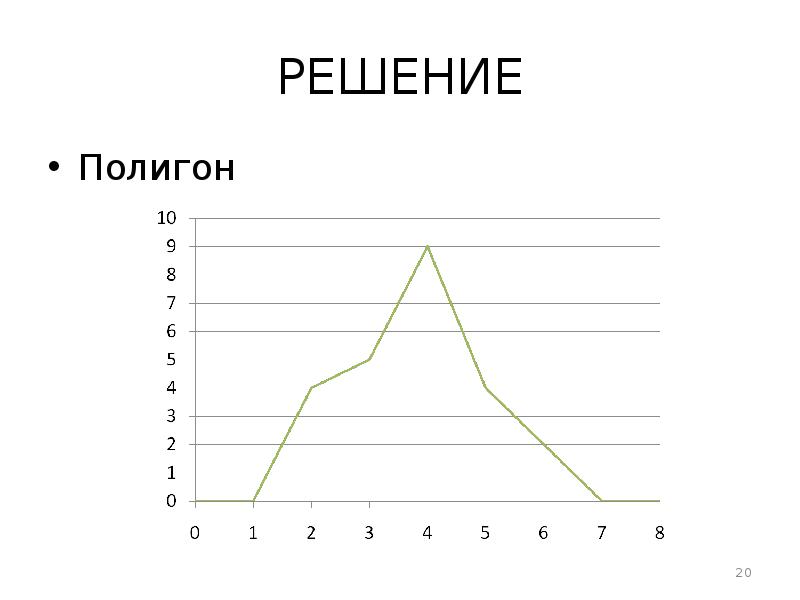
- 16. РЕШЕНИЕ 2. Дать графическое изображение дискретного ряда. Графическим изображением дискретного ряда
- 17. РЕШЕНИЕ отступить от левого края влево на одну варианту и от
- 18. РЕШЕНИЕ Полигон. Строится в прямоугольных системах координат. По оси абсцисс откладываются
- 19. РЕШЕНИЕ от начала координат до правого расширения разновидностей вариант, ось (0
- 20. РЕШЕНИЕ Полигон
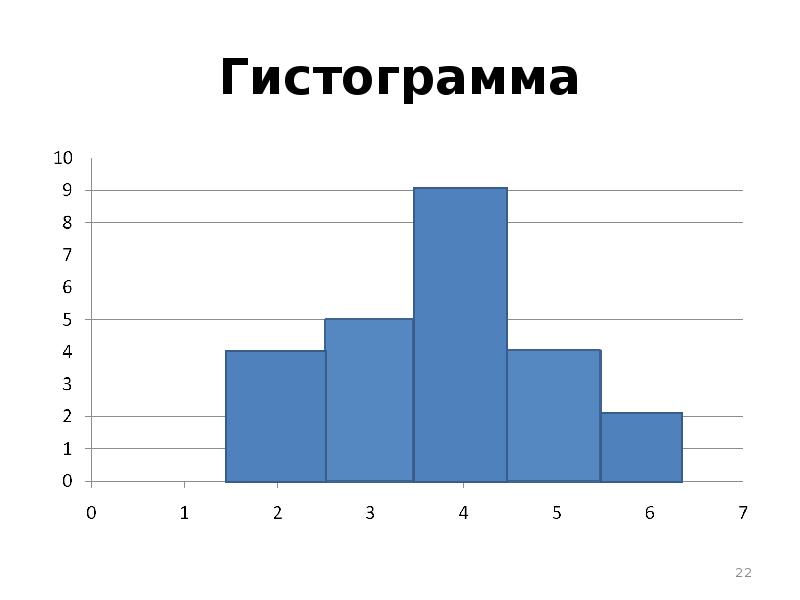
- 21. РЕШЕНИЕ Гистограмма. Это система прямоугольников, высоты которых равны значениям частот соответствующих
- 22. Гистограмма
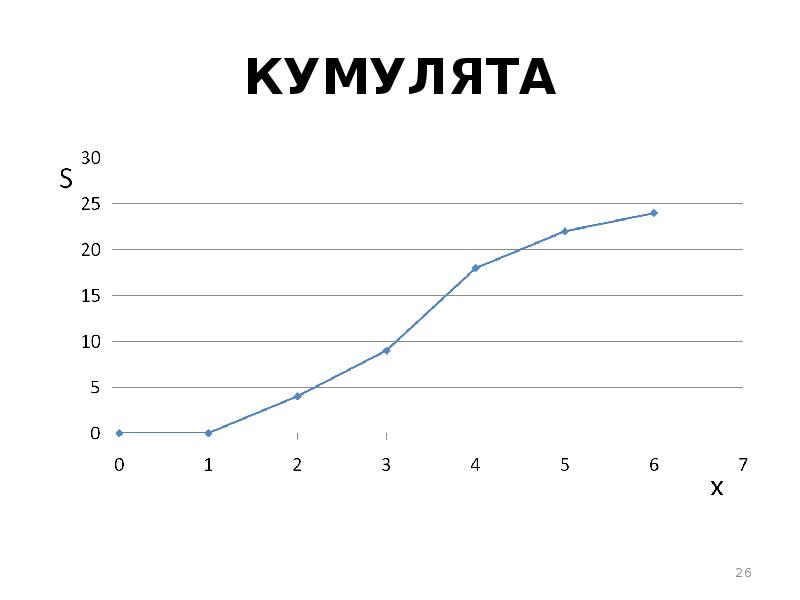
- 23. РЕШЕНИЕ Кумулята. Строится в прямоугольной системе координат, по оси абсцисс откладываются
- 24. РЕШЕНИЕ При нанесении точек необходимо пользоваться следующим правилом: левая граница расширения
- 25. РЕШЕНИЕ варианты равны значениям накопленных частот соответствующих групп. Полученные точки последовательно
- 26. КУМУЛЯТА
- 27. РЕШЕНИЕ 3. Вычислить показатели центра распределения, которым относятся МОДА, МЕДИАНА, СРЕДНЯЯ
- 28. РЕШЕНИЕ и среднюю арифметическую взвешенную:
- 29. РЕШЕНИЕ Мода (Мо) – это варианта, которая чаще всего встречается в
- 30. РЕШЕНИЕ Медиана (Ме) – это варианта, которая делит ряд распределения пополам,
- 31. РЕШЕНИЕ 4. Вычислить показатели вариации, к которым относятся: линейное отклонение
- 32. РЕШЕНИЕ Среднее линейное отклонение Среднее квадратическое отклонение
- 33. РЕШЕНИЕ Дисперсия Коэффициент вариации
- 34. РЕШЕНИЕ Вычислить показатели формы распределения (коэффициент асимметрии)
- 35. РЕШЕНИЕ При этом если Аs больше 0, то асимметрия правосторонняя, если
- 36. РЕШЕНИЕ
- 37. РЕШЕНИЕ
- 38. РЕШЕНИЕ
- 39. РЕШЕНИЕ
- 40. РЕШЕНИЕ
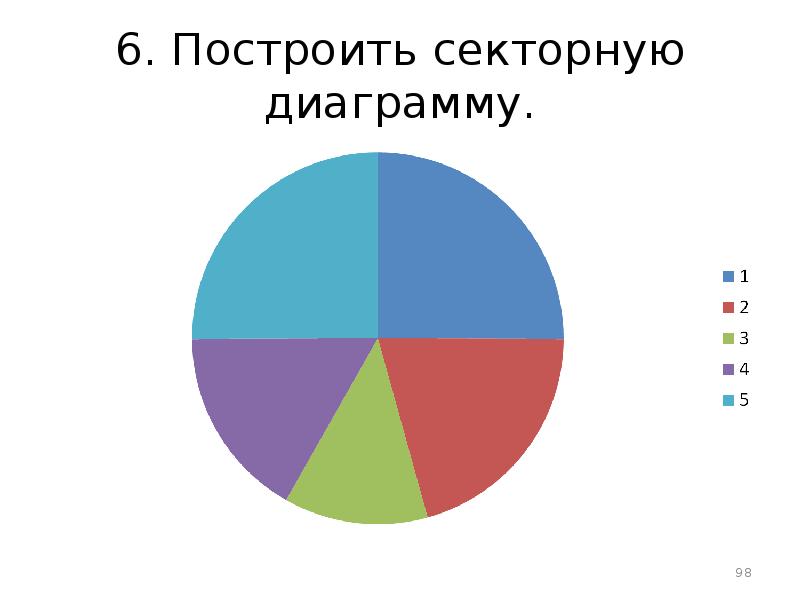
- 41. РЕШЕНИЕ Построить секторную диаграмму. Это круг разделенный радиусами на отдельные секторы.
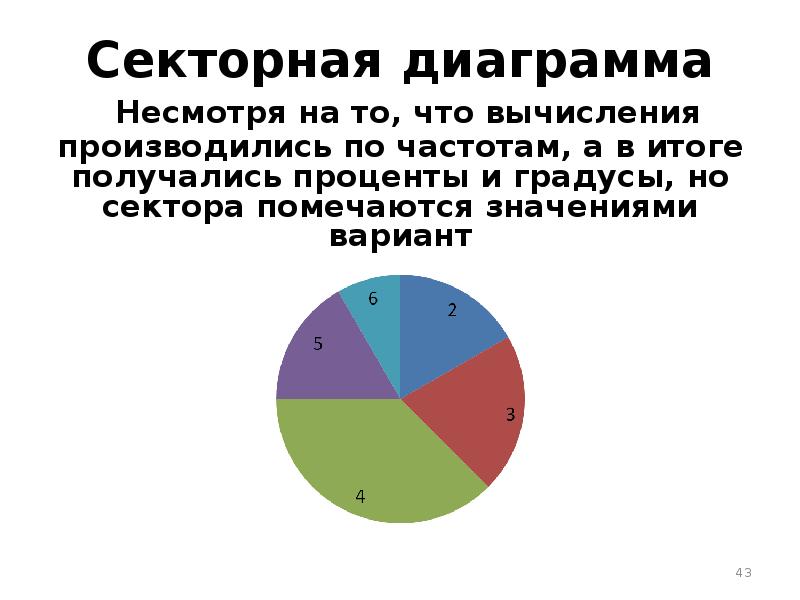
- 42. РЕШЕНИЕ Секторная диаграмма. Несмотря на то, что вычисления производились по частотам,
- 43. Секторная диаграмма Несмотря на то, что вычисления производились по частотам, а
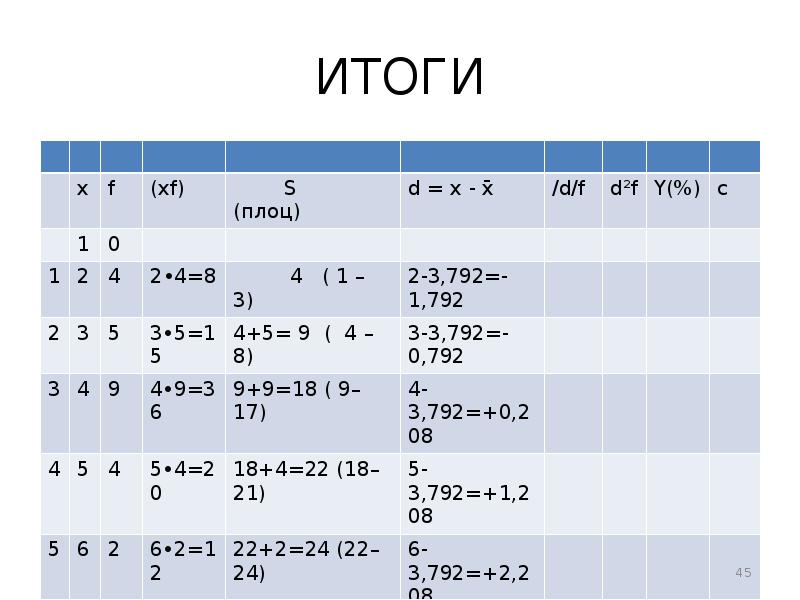
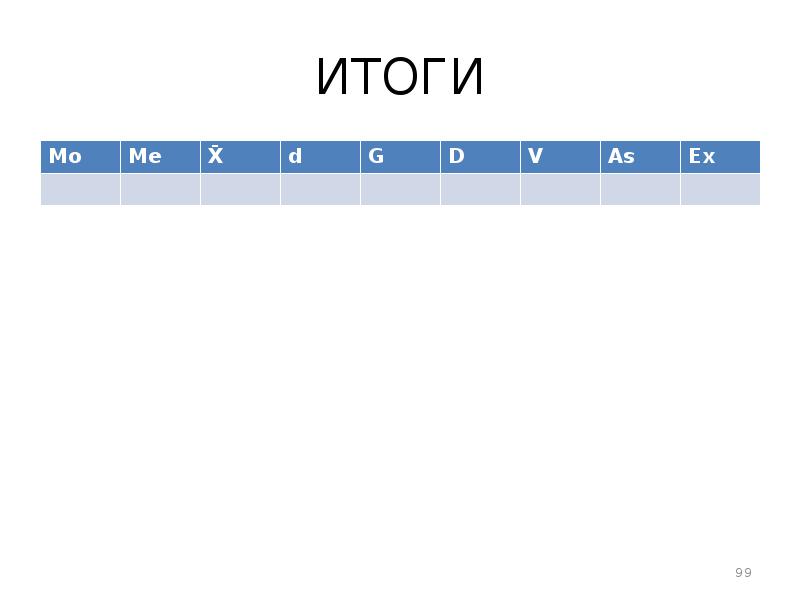
- 44. ИТОГИ Т.о. в результате решения задачи получены следующие результаты:
- 45. ИТОГИ
- 46. контрольная работа №1 1. Построить ряды распределения. 2. Дать графическое изображение
- 47. ЗАДАЧА № 2 ИНТЕРВАЛЬНЫЙ РЯД. Во второй части решения задачи необходимо
- 48. ТЕОРЕТИЧЕСКАЯ ПОДГОТОВКА 1. На первом этапе необходимо рассчитать интервал распределения, используя
- 49. 2. На втором этапе необходимо рассчитать центры распределения или интервалы распределения
- 50. ИСХОДНЫЕ ДАННЫЕ Варианты возраста рабочих (X) : 24 42 36 18
- 51. ИНТЕРВАЛ
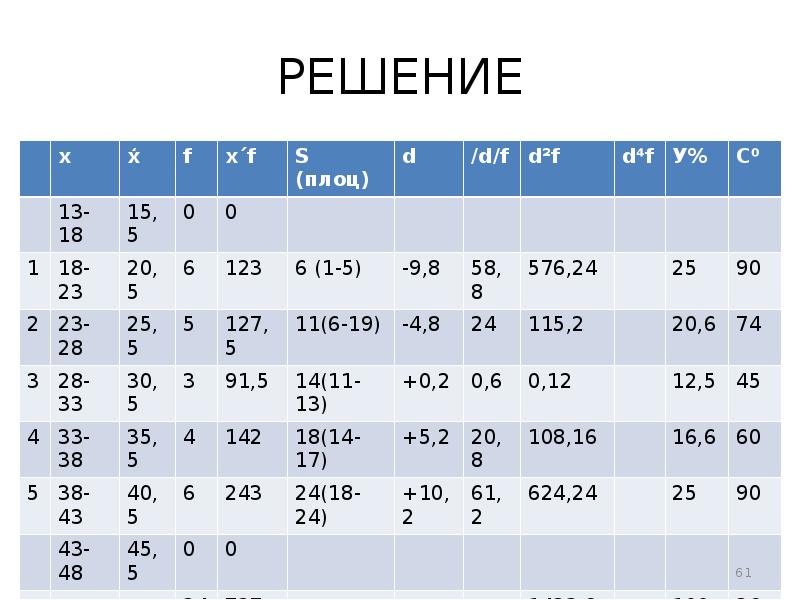
- 52. РЕШЕНИЕ 1. Построить интервальный ряд распределения в котором определить: интервалы границ
- 53. РЕШЕНИЕ Вторая группа. (23 – 28). Началом второй группы является правая
- 54. РЕШЕНИЕ Интервальные ряды также как дискретные необходимо подвергнуть расширению. При этом
- 55. СЕРЕДИНЫ ИНТЕРВАЛОВ
- 56. РЕШЕНИЕ Середины интервалов определяются следующим образом: Первая группа: 20,5 Вторая
- 57. РЕШЕНИЕ Частоты рассчитываются следующим образом. Каждой группе принадлежат варианты, которые по
- 58. РЕШЕНИЕ Во второй группе варианты: 24 25 26 23 27, т.е.
- 59. РЕШЕНИЕ Накопленные частоты определяются по стандартной схеме. Первая группа:
- 60. РЕШЕНИЕ Распределение накопленных частот по правилу (плоц). Первая группа: (1
- 61. РЕШЕНИЕ
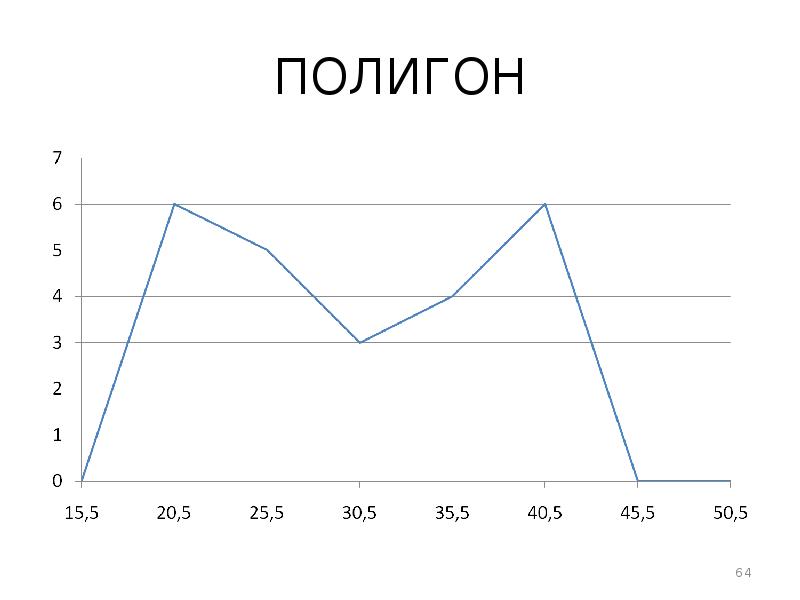
- 62. РЕШЕНИЕ 2. Дать графическое изображение интервального ряда. Графически интервальный ряд распределения
- 63. РЕШЕНИЕ По оси ординат откладываются значения частот, т.е. от 0 до
- 64. ПОЛИГОН
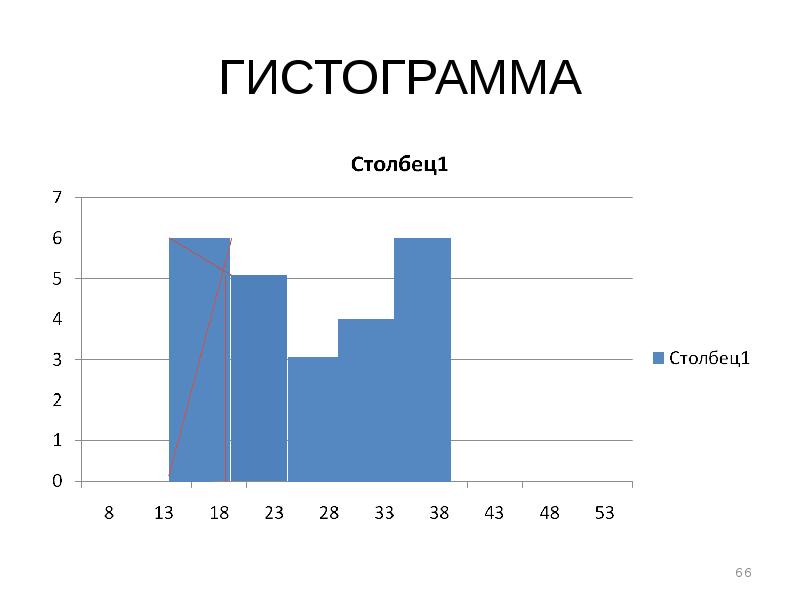
- 65. РЕШЕНИЕ Гистограмма. Координатные оси соответствуют полигону. Однако в интервальном ряду прямоугольники
- 66. ГИСТОГРАММА
- 67. РЕШЕНИЕ С помощью гистограммы можно определить значение графической моды. Для этого
- 68. РЕШЕНИЕ Возникает вопрос. Какой прямоугольник является модальным? Модальным является прямоугольник, соответствующий
- 69. РЕШЕНИЕ Из точки пересечения полученных отрезков опустить перпендикуляр на ось абсцисс,
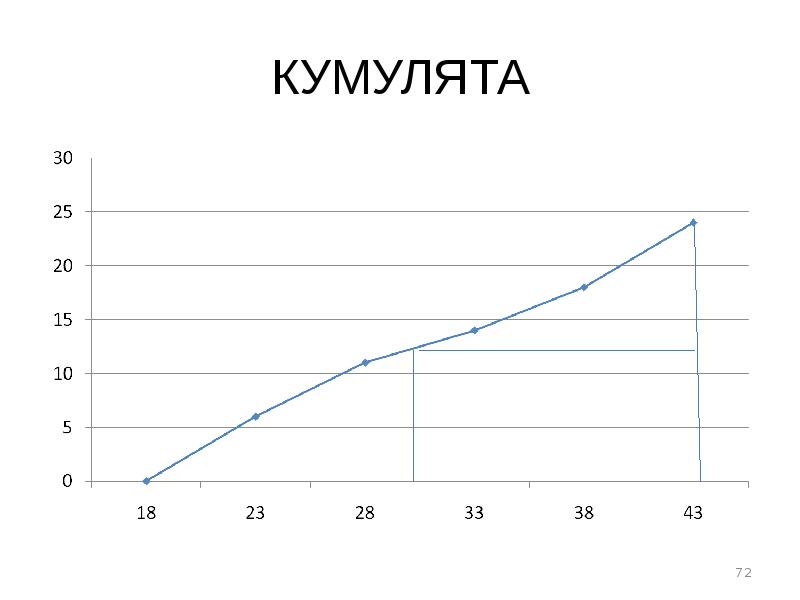
- 70. Кумулята. Строится в прямоугольных системах координат. По оси абсцисс откладываются значения
- 71. РЕШЕНИЕ Полученные точки соединяются прямыми линиями слева направо. С помощью кумуляты
- 72. КУМУЛЯТА
- 73. РЕШЕНИЕ Вычислить показатели центра распределения к которым относятся средняя арифметическая, мода,
- 74. РЕШЕНИЕ Средняя арифметическая взвешенная:
- 75. РЕШЕНИЕ Мода в интервальном ряду:
- 76. Х(Мо) – модальная варианта, левая граница модального интервала, а модальный интервал
- 77. f(Mo) – модальная частота, т.е. максимальная частота, которая равна 6. f(Mo)
- 78. РЕШЕНИЕ Первая мода:
- 79. РЕШЕНИЕ Вторая мода:
- 80. РЕШЕНИЕ Медиана в интервальном ряду определяется по следующей формуле:
- 81. РЕШЕНИЕ Х(Ме) – левая граница медианного интервала, который определяется по номеру
- 82. РЕШЕНИЕ f(Ме) – частота медианного интервала. i – интервал распределения. n
- 83. РЕШЕНИЕ Медиана равна:
- 84. РЕШЕНИЕ 4. Вычислить показатели вариации, к которым относятся: линейное отклонение:
- 85. РЕШЕНИЕ среднее линейное отклонение:
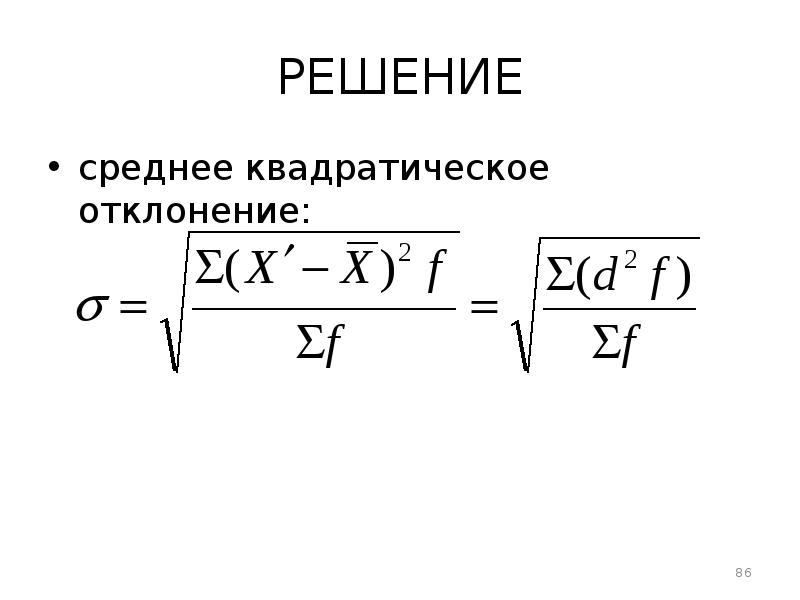
- 86. РЕШЕНИЕ среднее квадратическое отклонение:
- 87. РЕШЕНИЕ дисперсия:
- 88. РЕШЕНИЕ Коэффициент вариации:
- 89. РЕШЕНИЕ 5. Вычислить показатели формы распределения, к которым относятся: коэффициент асимметрии:
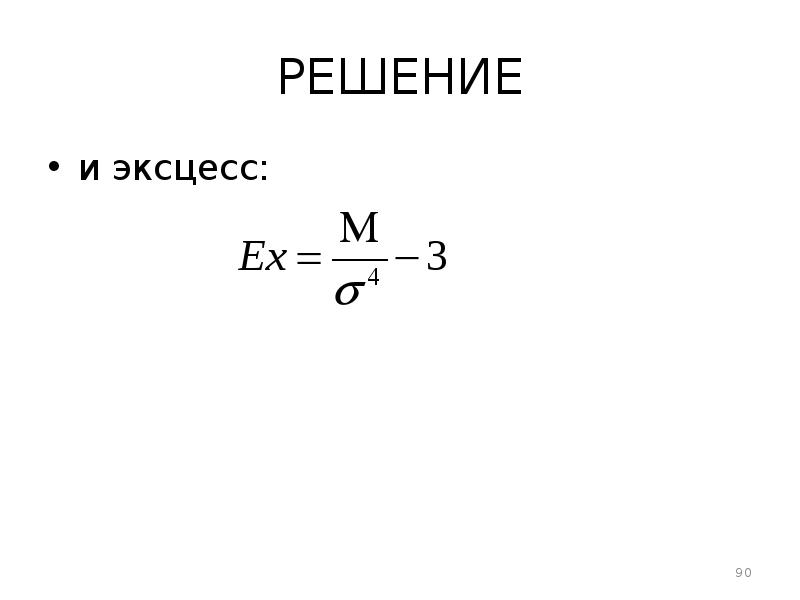
- 90. РЕШЕНИЕ и эксцесс:
- 91. РЕШЕНИЕ М – момент четвертого порядка, который определяется по следующей формуле:
- 92. РЕШЕНИЕ
- 93. РЕШЕНИЕ
- 94. РЕШЕНИЕ
- 95. РЕШЕНИЕ
- 96. РЕШЕНИЕ Показатели асимметрии
- 97. РЕШЕНИЕ Аs(1) = +1,039 Аs(2) = -1,163 М = 5245,576
- 98. 6. Построить секторную диаграмму.
- 99. ИТОГИ
- 100. КОНТРОЛЬНАЯ РАБОТА №2 X(min) = HB + 20 X(max) = HB
- 101. Скачать презентацию




























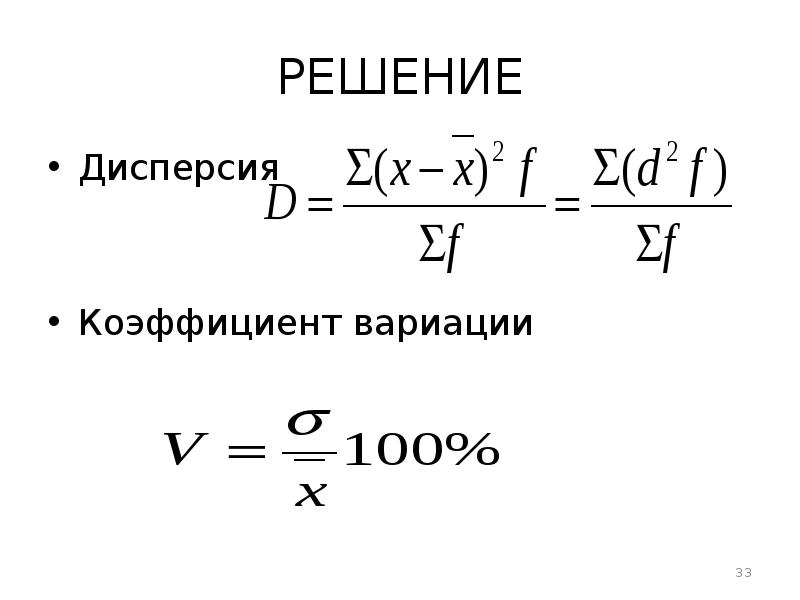













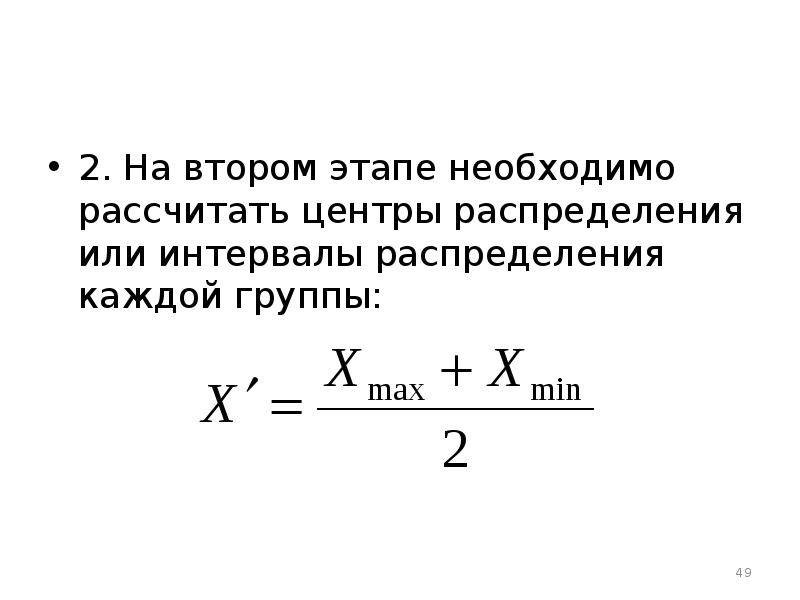
































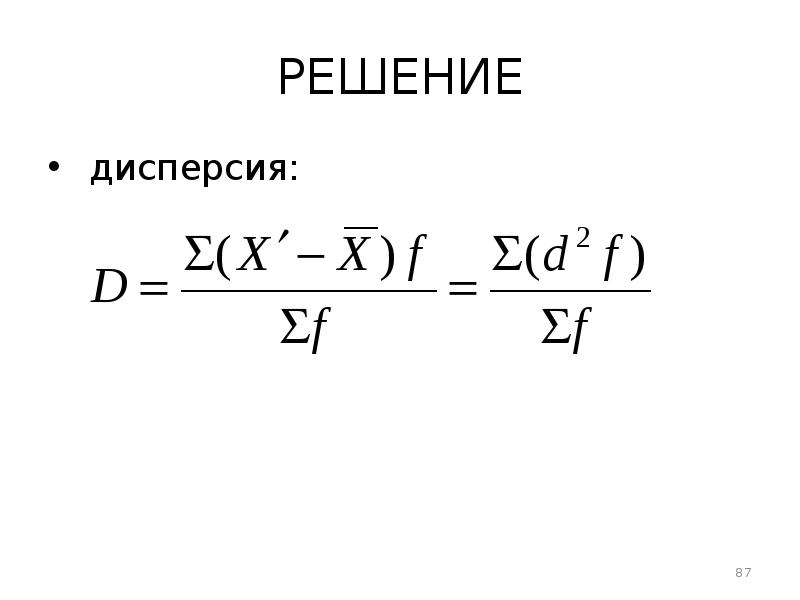










Слайды и текст этой презентации
Похожие презентации





























