Обернені задачі моделювання. Моделювання фізичних процесів презентация
Содержание
- 2. Практичні задачі моделювання Є модель, є вхідні дані, є вихідні дані
- 3. Де таке виникає? Томографічна реконструкція Спектроскопія Надрозрізнення Непрямі вимірювання Локація …
- 4. Нехай є математична модель
- 5. Пряма задача Пряма задача моделювання – знайти значення характеристики при певних
- 6. Пряма задача термодеструкції
- 7. Пряма задача переносу рентгенівського випромінювання
- 8. Не прямі задачі Обернена задача Задача синтезу Задача оптимізації
- 9. Обернена задача Знайти вхідні параметри, при яких досягаються задані вихідні значення
- 10. Обернена задача Знайти функцію джерела термодетрукції, яка задає заданий розподіл температури
- 11. Задача синтезу Знайти модель, яка для заданих вхідних значень дає задані
- 12. Задача синтезу для переносу рентгенівського випромінювання Знайти яка повинна бути установка,
- 13. Задача синтезу для ЯМР томографії Знайти розподіл магнітного поля (імпульсну послідовність),
- 14. Задача оптимізації Знайти всі параметри, при яких заданий цільовий функціонал має
- 15. Оптимізація При яких параметрах задачі, що реалізуються на практиці, розподіл температур
- 16. Особливості не прямих задач Може не існувати розв’язку Може існувати багато
- 17. Цікавий факт Прямі задачі та задачі оптимізації найчастіше розв’язуються так, як
- 18. Приклади нестійких задач Часто задача має розв’язок, але нестійка до вхідних
- 19. Задача спектроскопії
- 20. Чому ця задача нестійка?
- 21. Які ще задачі нестійкі? Інтегральні рівняння першого роду Системи лінійних рівнянь
- 22. Коректно та некоректно поставлені задачі Задача називається коректно поставленою (за Адамаром),
- 23. Страшна проблема Питання: що робити, якщо виникла некоректна задача, яка
- 24. Розв’язання некоректних задач Звести задачу до коректно поставленої, розв’язок якої близький
- 25. Співставлення за точністю Зміна задачі змінює розв’язок Реальні вхідні дані
- 26. Деякі методи для задач оптимізації (коректних) Зворотне керування Лінійне та нелінійне
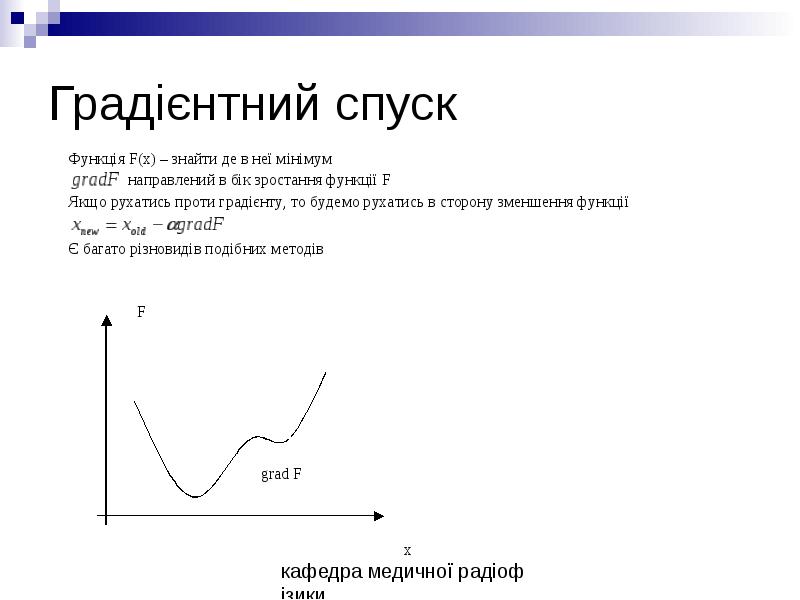
- 27. Градієнтний спуск
- 28. Деякі методи для зворотних задач, задач синтезу та інших некоректних Розв’язання
- 29. Регуляризація за Тихоновим Теорема Тихонова Якщо розв’язок заданий на компакті (обмежена,
- 30. Регуляризація за Тихоновим Задача змінюється так, щоб розв’язок був заданий на
- 31. Приклади регуляризації за Тихоновим Метод підбору Метод квазі (псевдо) розв’язку Псевдо-обернена
- 32. Метод підбору
- 33. Метод псевдорозв’язку
- 34. Псевдо-обернена матриця Мура Пенроуза
- 35. Метод заміни рівняння близьким до нього
- 36. Метод урізаного сингулярного розвинення (метод головних компонент) Потужний метод для перевизначених
- 37. Метод Лагранжа Задача замінюється варіаційної
- 38. Нормальний розв’язок системи лінійних рівнянь
- 39. Метод ітерацій
- 40. Метод параметричної регресії Створюється проста модель з невідомими параметрами Параметри підбираються
- 41. Задача При томографії твердого тіла час поперечної релаксації дуже малий Чи
- 42. Реконструкція спінової густини і часу поперечної релаксації за сигналом Фур’є томографа
- 43. Дискретизація задачі Час і просторові координати замінюємо дискретним набором параметрів
- 44. Розв’язок Рівняння замінюємо варіаційною задачею на екстремум
- 45. Метод Проні Прямий розв’язок варіаційної задачі складний, оскільки рівняння нелінійні Треба
- 46. Метод Проні
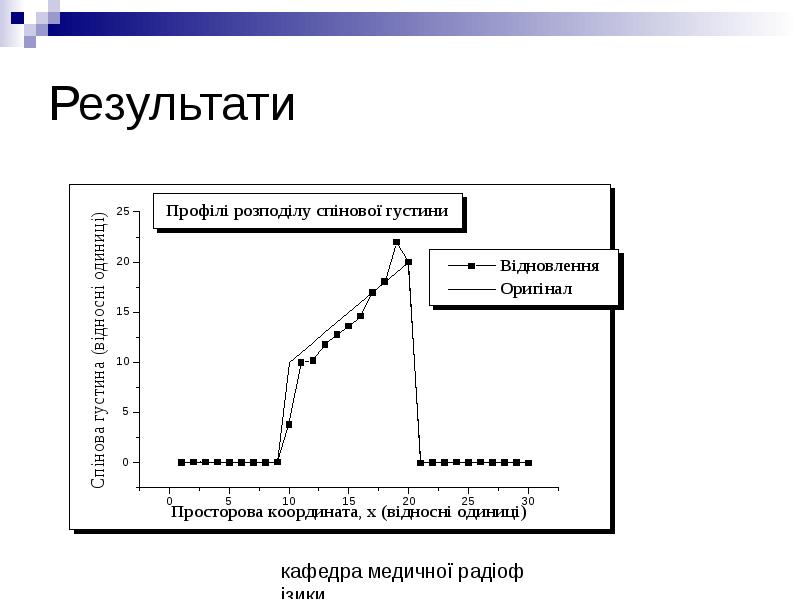
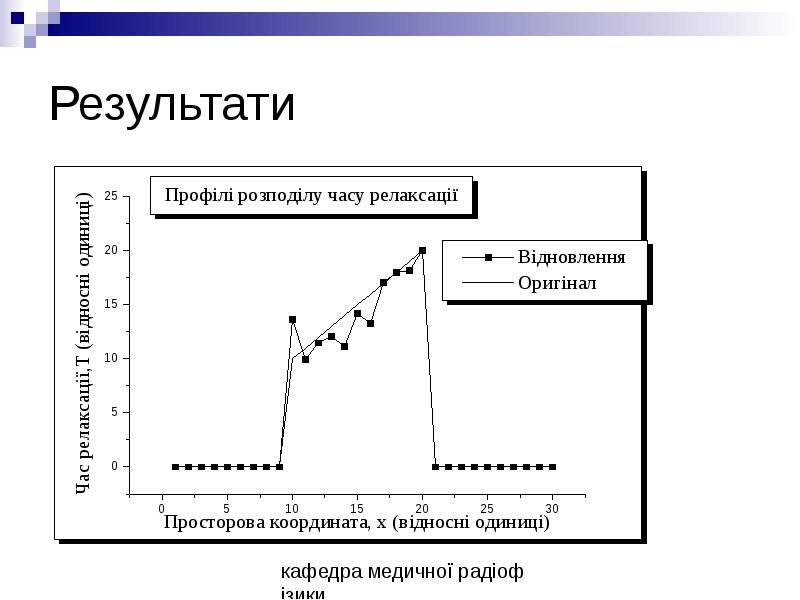
- 47. Результати
- 48. Результати
- 49. Висновки Зворотні задачі та задачі синтезу – некоректні Для розв’язку таких
- 50. Питання
- 51. Скачать презентацию















































Слайды и текст этой презентации
Скачать презентацию на тему Обернені задачі моделювання. Моделювання фізичних процесів можно ниже:
Похожие презентации