Обыкновенные дифференциальные уравнения. Теорема существования. (Лекция 2.7) презентация

Лекция 2.7. 12. Обыкновенные дифференциальные уравнения. 12.1. Дифференциальные уравнения 1-го порядка. 12.1.1. Общие понятия. Теорема существования. Простейшие дифференциальные уравнения: или Решение Более сложные дифференциальные уравнения: и т.д. или и т.д.

Определение. Дифференциальным уравнением 1-го порядка называется уравнение, связывающее независимую переменную функцию и ее производную Будем рассматривать дифференциальные уравнения функции одной переменной. Общий вид дифференциального уравнения 1-го порядка или

Определение. Решением дифференциального уравнения называется функция, которая при подстановке ее вместе с производной в это уравнение превращает его в тождество. Примеры: 1) Решение где - произвольная постоянная. 2) Решение

Дифференциальное уравнение 1-го порядка имеет бесчисленное множество решений, которые обычно определяются формулой содержащей одну произвольную постоянную. Такое множество решений называют общим решением дифференциального уравнения. Придавая определенные (допустимые) значения, получим частные решения. При решении конкретных задач нас будет интересовать частное решение, определяемое начальными условиями. Обычно начальные условия задаются парой значений или Задача отыскания частного решения по начальному условию называется задачей Коши.

Теорема Коши о существовании и единственности решения. Пусть дано дифференциальное уравнение и начальное условие Если функция и ее частная производная непрерывны в открытой области, содержащей точку то в достаточно малом интервале это уравнение имеет единственное решение удовлетворяющее заданному начальному условию Без доказательства.

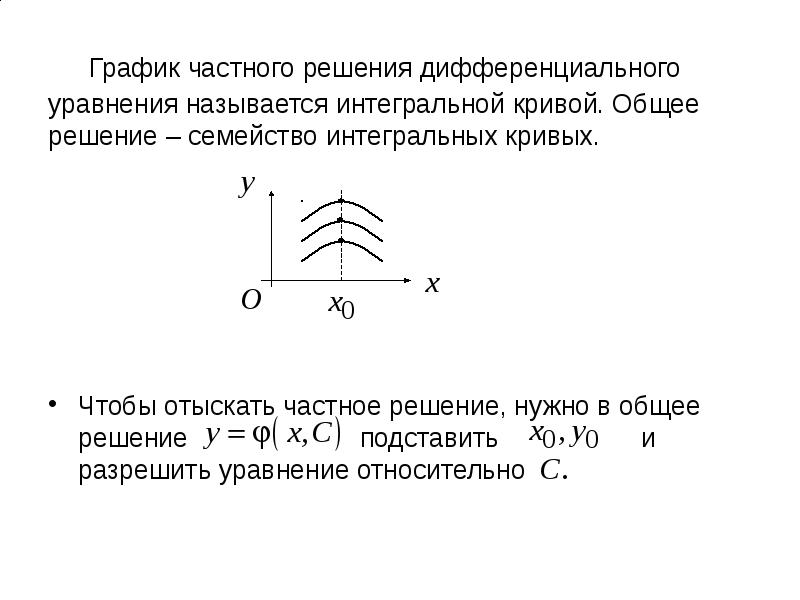
График частного решения дифференциального уравнения называется интегральной кривой. Общее решение – семейство интегральных кривых. Чтобы отыскать частное решение, нужно в общее решение подставить и разрешить уравнение относительно

Примеры: 1) Дифференциальное уравнение Общее решение Начальное условие Подставим начальное условие в общее решение дифференциального уравнения. Получим алгебраическое уравнение для определения произвольной постоянной Следовательно Частным решением дифференциального уравнения, удовлетворяющим начальным условиям будет

2) Дифференциальное уравнение Общее решение Начальное условие Подставим начальное условие в общее решение дифференциального уравнения. Получим Частным решением дифференциального уравнения, удовлетворяющим начальным условиям будет

3) Дифференциальное уравнение Общее решение Начальное условие Подставим начальное условие в общее решение дифференциального уравнения. Получим Частным решением дифференциального уравнения, удовлетворяющим начальным условиям будет Общее решение дифференциального уравнения может быть получено и в неявном виде

12.1.2. Дифференциальные уравнения с разделяющимися переменными. Рассмотрим дифференциальное уравнение Проинтегрировав, получим Если то Пример:

Определение. Дифференциальные уравнения, в которых переменные можно разделить посредством умножения или деления обеих частей уравнения на одно и то же выражение, называются дифференциальными уравнениями с разделяющимися переменными. Внимание! Может произойти потеря частного решения.

Пример. Рассмотрим дифференциальное уравнение Разделим переменные Потеряли частное решение

12.1.3. Физические задачи, приводящие к дифференциальным уравнениям. 1) Радиоактивный распад. Экспериментально установлено, что скорость распада пропорциональна количеству не распавшегося вещества. В момент Период полураспада Тогда Следовательно - определяется экспериментально.

2) Охлаждение тела. Скорость охлаждения тела пропорциональна разности между температурой тела и температурой окружающей среды Окончательно

12.1.4. Однородные дифференциальные уравнения. Определение. Дифференциальное уравнение называется однородным, если функция может быть представлена, как функция отношения своих аргументов Пример.

Функция называется однородной функцией измерения если Примеры: 1) - 1-й порядок однородности. 2) - 2-й порядок однородности. 3) - нулевой порядок однородности (просто однородная функция) Пример приведения функции.

Дифференциальное уравнение где однородная функция нулевого измерения, можно преобразовать к уравнению с разделяющимися переменными. Введем вспомогательную функцию или Тогда Вычислив интеграл, и перейдя к получим Предполагается, что Если то

Пример. Тогда Проинтегрировав, получим или Окончательно