Оценки параметров генеральной совокупности презентация

Дисциплины: «Теория вероятностей», «Математическая статистика», «Теория вероятностей и математическая статистика» Тема: Оценки параметров генеральной совокупности

Домашнее задание (проверка) 16. Для вариационного ряда Найдем математическое ожидание, дисперсию, вариацию:

Точечные оценки параметров Пусть случайная величина Х имеет закон распределения, зависящий от параметра θ (тэта): F(x,θ). О величине параметра можно судить по конечной выборке из генеральной совокупности. Оценкой параметра θ называется любая функция от значений выборки , т.е. статистика. Статистику можно рассматривать как случайную величину. Ее нужно выбирать таким образом, чтобы ее значения точнее оценивали значение неизвестного параметра θ. Оценка называется несмещенной, если ее математическое ожидание . Для несмещенных оценок устраняется возможность появления систематической ошибки при оценивании параметра θ. Оценка называется состоятельной, если она удовлетворяет закону больших чисел, т.е. предел по вероятности . Несмещенная оценка называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок этого параметра, т.е. дисперсия

Точечные оценки параметров Оценки называются точечными, так как они оценивают одно численное значение параметра (точку). Пусть генеральные параметры распределения для случайной величины Х будут (математическое ожидание) и (дисперсия). Тогда для повторной выборки: выборочное среднее является несмещенной, состоятельной и эффективной оценкой параметра а: выборочная дисперсия является смещенной, состоятельной оценкой параметра : , причем исправленная выборочная дисперсия является несмещенной, состоятельной оценкой параметра :

Точечные оценки параметров выборочная доля является несмещенной, состоятельной и эффективной оценкой генеральной доли р: Для указанных оценок справедливы формулы: Для повторной выборки дисперсии Для бесповторной выборки дисперсия

Пример 1: Из 1500 деталей отобрано 250, распределение которых по размеру Х задано в таблице: Найти точечные оценки для среднего и дисперсии, а также дисперсию оценки среднего при повторном и бесповторном отборах. Решение. Вычислим по формулам (используем середины интервалов сi, число интервалов r=6, объем выборки n=250):

Пример 1 (продолжение): Вычислим дисперсию оценки среднего: для повторной выборки: для бесповторной выборки

Пример 2: Выборочно обследовали партию кирпича. Из 100 проб в 12 случаях кирпич оказался бракованным. Найти оценку доли бракованного кирпича и дисперсию этой оценки. Решение. По условию задачи число бракованных изделий m=12, объем выборки n=100, тогда оценкой доли бракованных является выборочная доля Дисперсия этой оценки для повторной выборки равна А среднее квадратическое отклонение этой оценки равно

Метод наименьших квадратов для нахождения точечных оценок: Исследуется зависимость двух случайных величин Y и Х по их выборкам и . Пусть выбранный вид функции ϕ, устанавливающей эту зависимость, содержит параметры , i=1,2,…,k, тогда их оценки выбираются так, чтобы функция принимала минимальное значение. Из необходимого условия экстремума следует решение системы уравнений:

Пример 3: Найти оценки параметров a и b по результатам выборочного наблюдения, если связь между случайными величинами Y и X линейна: . Объем выборки равен n. Решение. Используем метод наименьших квадратов. Построим функцию и найдем ее минимум. Вычислим частные производные и положим их равными нулю: Решим эту систему относительно a и b:

Пример 3 (продолжение): Разделим оба равенства на n и обозначим выборочные средние: Тогда получим систему линейных алгебраических выражений: Эту систему можно решить любым известным методом (Гаусса, Кремера, матричным): Окончательно получим оценки:

Интервальные оценки параметров Интервальная оценка параметра дает возможность определить точность и надежность его оценки. Интервальной оценкой параметра θ называется интервал (α,β), который с заданной вероятностью γ (гамма) накрывает неизвестное значение этого параметра. Интервал (α,β) называется доверительным интервалом, вероятность γ - доверительной вероятностью или уровнем надежности.

Интервальные оценки параметров Обычно доверительный интервал симметричен относительно точечной оценки , т.е. имеет вид , где Δ - предельная ошибка выборки. Причем вероятность . Рассмотрим генеральную совокупность объема N и выборку из нее . Для нее имеем: выборочное среднее – выборочную дисперсию – выборочную долю признака – которым в выборке обладают m элементов. Рассмотрим следующие интервальные оценки:

1. Доверительный интервал для генеральной средней а а) для повторной выборки б) для бесповторной выборки Величина t определяется: при n>30 из функции Лапласа Ф(t)=γ, при n≤30 из вероятности , где ξ имеет распределение Стьюдента для (n-1) степени свободы.

Пример 4: Для определения среднего процентного содержания белка в зернах пшеницы было отобрано 625 зерен, обследование которых показало, что выборочное среднее равно 16,8, а выборочная дисперсия равна 4. Чему равна с вероятностью 0,988 предельная ошибка выборки? Решение. По условию задачи . Так как генеральная совокупность бесконечна, то используем формулу для повторной выборки при определении предельной ошибки: Значение t найдем из условия Ф(t)=γ, т.е. Ф(t)=0,988. По таблице значений функции Лапласа найдем: t=2,51. Найдем предельную ошибку

Пример 5: Выборочное среднее квадратическое отклонение десяти измерений некоторой величины равно 10 см. Найти с надежностью γ=0,6 предельную ошибку выборки. Решение. Здесь n=10<30 и выборка повторная, S=10. По таблицам распределения Стьюдента для γ=0,6 и степени свободы n-1=9 находим t=0,88. Тогда получим предельную ошибку выборки

Пример 6: Из партии в 5000 электрических ламп было отобрано 300 по схеме бесповторной выборки. Средняя продолжительность горения ламп в выборке оказалась равной 1450 часам, а дисперсия – 4000. Найти доверительный интервал для среднего срока горения лампы с надежностью 0,9996. Решение. По условию задачи γ=0,9996 и объем выборки n=300>30, тогда по таблице значений функции Лапласа находим t из условия Ф(t)=0,9996: t=3,57. Применим формулу , где и вычислим предельную ошибку Искомый доверительный интервал будет равен:

2. Доверительный интервал для генеральной доли признака р: а) для повторной выборки б) для бесповторной выборки Величина t определяется из функции Лапласа Ф(t)=γ.

Пример 7: В партии, содержащей 5000 изделий, проверено 400. Среди них оказалось 300 изделий высшего сорта. Найти с надежностью 0,95 доверительный интервал для доли изделий высшего сорта в случаях повторной и бесповторной выборок. Решение. По условию задачи имеем: По значению функции Лапласа Ф(t)=0,95 определим t=1,96. 1) Для повторной выборки предельная ошибка доли равна Тогда доверительный интервал равен: 2) Для бесповторной выборки предельная ошибка доли равна Тогда доверительный интервал равен:

Пример 8: Среди стандартных изделий одной фабрики в среднем 15% относится ко второму сорту. С какой вероятностью можно утверждать, что процент изделий второго сорта среди 1000 стандартных изделий данной фабрики отличается от 15% не более чем на 2%? Решение. По условию задачи имеем n=1000, w=15%/100%=0,15, Δ=2%/100%=0,02. Требуется найти вероятность Найдем t из формулы , тогда Используя значения из таблицы функции Лапласа найдем

3. Доверительный интервал для генеральной дисперсии Где и определяются из условия Обычно они определяются так, чтобы Тогда по таблице распределения Хи-квадрат со степенью свободы (n-1) они определяются из условий

Пример 9: Признак Х генеральной совокупности распределен нормально. Имеется выборка в виде таблицы Найти доверительный интервал, накрывающий среднее квадратическое отклонение с вероятностью 0,99. Решение. Вычислим выборочные характеристики:

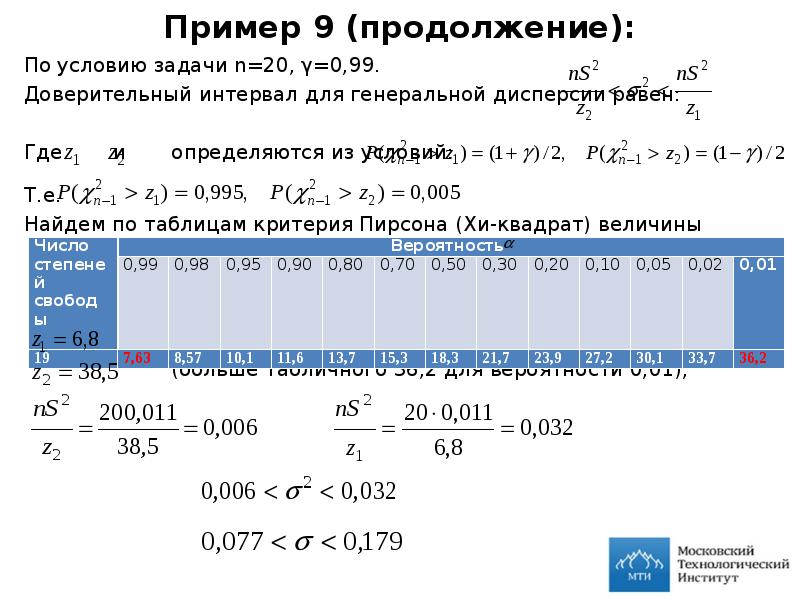
Пример 9 (продолжение): По условию задачи n=20, γ=0,99. Доверительный интервал для генеральной дисперсии равен: Где и определяются из условий: Т.е. Найдем по таблицам критерия Пирсона (Хи-квадрат) величины (меньше табличного 7,63 для вероятности 0,99), (больше табличного 36,2 для вероятности 0,01),

4. Объем выборки n, необходимый для достижения требуемой надежности γ При параметре а повторная выборка – бесповторная выборка – 2) При параметре р повторная выборка – бесповторная выборка – Замечание: При N→ в бесконечность, формулы для бесповторной выборки совпадут с формулами для повторной выборки.

Пример 10: Найти объемы повторной и бесповторной выборок из 10000 банок консервов для определения доли банок, не соответствующих стандарту. Предполагается, что предельная ошибка выборки не превосходит 0,05 с доверительной вероятностью 0,9995. Решение. По условию задачи N=10000, Δ=0,05, γ=0,9995. По таблице значений функции Лапласа Ф(t)=0,9995 найдем t=3,5. 1) Для повторной выборки объем равен Так выборочная доля w по условию задачи неизвестна, тогда выберем его таким, чтобы выражение w(1-w) было максимальным. Это условие достигается при w=0,5 (вычислим производную функции и положим ее равной нулю: (w(1-w))’=1-2w=0 ). Тогда завышенное значение n будет равно n=4900*0,5*0,5=1225.

Пример 10 (продолжение): Для бесповторной выборки объем равен В этом случае наибольшее значение выражения w(1-w) соответствует максимальному n. Положим w=0,5, тогда Вопрос: Для расчета средней арифметической статистической совокупности используется формула (n – объем выборки, xi – выборочные значения): 1) 2) 3)

Тестовые вопросы 1. Характеристикой оценок числовых характеристик по результатам выборочных значений является: а) репрезентативность оценки; б) несмещенность оценки; в) сходимость любой оценки к математическому ожиданию теоретического распределения; г) независимость оценки от объема выборки. 2. Определение искомой характеристики генеральной совокупности внутри какого-то интервала с заданной вероятностью, называется а) интервальной оценкой; б) точечной оценкой; в) выборочной оценкой; г) качественной оценкой.

Тестовые вопросы 3. Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид … а) (10,6; 13,4) б) (12; 13,7) в) (10,8; 12) г) (11,2; 11,8) 4. Точечная оценка математического ожидания нормального распределения равна 15. Тогда его интервальная оценка может иметь вид... а) (13,8; 15) б) (13,8; 16,2) в) (15; 16,2) г) (13,8; 14,1)

Тестовые вопросы 5. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 10, 13, 13. Тогда несмещенная оценка дисперсии измерений равна: а) 6; б) 2; в) 12; г) 3. 6. По городской телефонной сети было произведено 100 наблюдений и установлено, что средняя продолжительность телефонного разговора составляет 4 минут при среднеквадратичном отклонении 2 мин. Предельная ошибка выборки с вероятностью 0,954 составляет а) 0,2; б) 0,3; в)  0,4; г) 0,5.

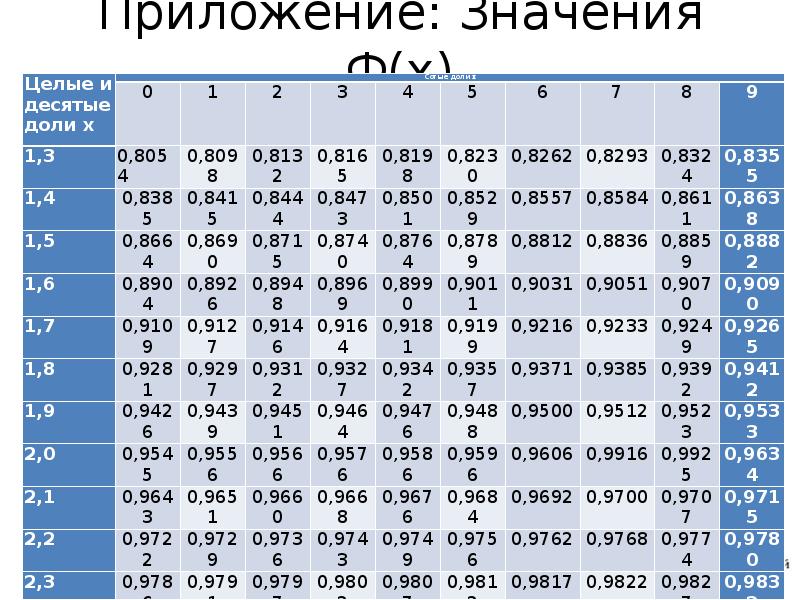
Приложение: Значения Ф(х)

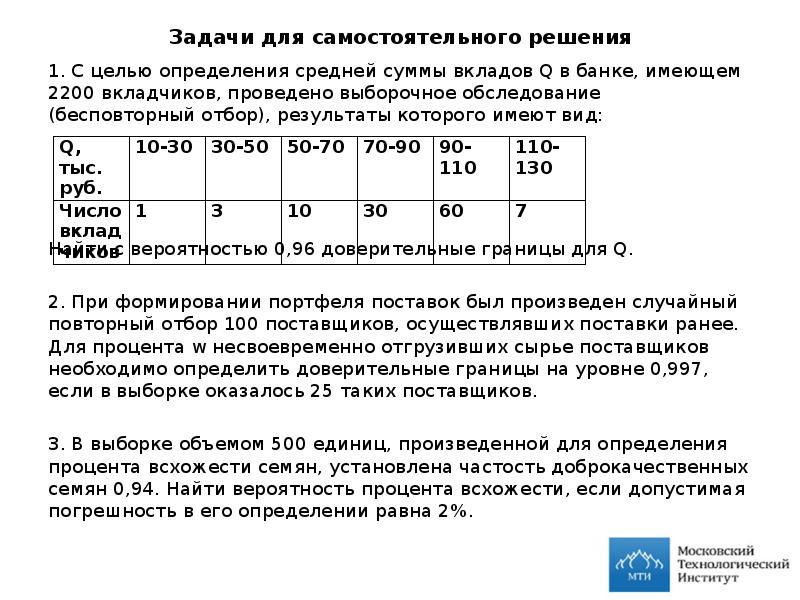
Задачи для самостоятельного решения 1. С целью определения средней суммы вкладов Q в банке, имеющем 2200 вкладчиков, проведено выборочное обследование (бесповторный отбор), результаты которого имеют вид: Найти с вероятностью 0,96 доверительные границы для Q. 2. При формировании портфеля поставок был произведен случайный повторный отбор 100 поставщиков, осуществлявших поставки ранее. Для процента w несвоевременно отгрузивших сырье поставщиков необходимо определить доверительные границы на уровне 0,997, если в выборке оказалось 25 таких поставщиков. 3. В выборке объемом 500 единиц, произведенной для определения процента всхожести семян, установлена частость доброкачественных семян 0,94. Найти вероятность процента всхожести, если допустимая погрешность в его определении равна 2%.

Задачи для самостоятельного решения 4. Сколько лиц в возрасте от 19 до 24 лет надо опросить, чтобы установить средний процент студентов с точностью до 0,5%? 5. Определить численность выборки при обследовании остатков на расчетных счетах у клиентов банка, чтобы с вероятностью 0,683 предельная ошибка равнялась 5 усл. ед., если усл. ед. 6. Из 2500 ящиков продукции было проверено 10%. Среди них оказалось 80% ящиков с продукцией первого сорта. Найти границы, в которых с вероятностью 0,996 заключена доля ящиков с продукцией первого сорта. 7. По данным 10 измерений некоторой величины найдено ее выборочное среднее значение 20 и выборочная исправленная дисперсия 25. Найти границы, в которых с вероятностью 0,99 заключено истинное значение измеряемой величины. Найти с вероятностью 0,99 доверительный интервал для дисперсии генеральной совокупности этой величины.