Основы корреляционного анализа презентация
Содержание
- 2. Многомерный корреляционный анализ При исследование реальных экономических явлений приходится сталкиваться с
- 3. Многомерный корреляционный анализ Закон распределения не известен Обычно ограничиваются
- 4. Многомерный корреляционный анализ Ковариационная матрица позволяет строить и анализировать
- 5. Ковариация Ковариация Для устранения недостатка ковариации был введён линейный коэффициент
- 6. Основатели корреляционного анализа Карл (Чарлз) Пирсон (Karl (Charles) Pearson)
- 7. Ковариация Ковариация Коэффициент корреляции рассчитывается по формуле:
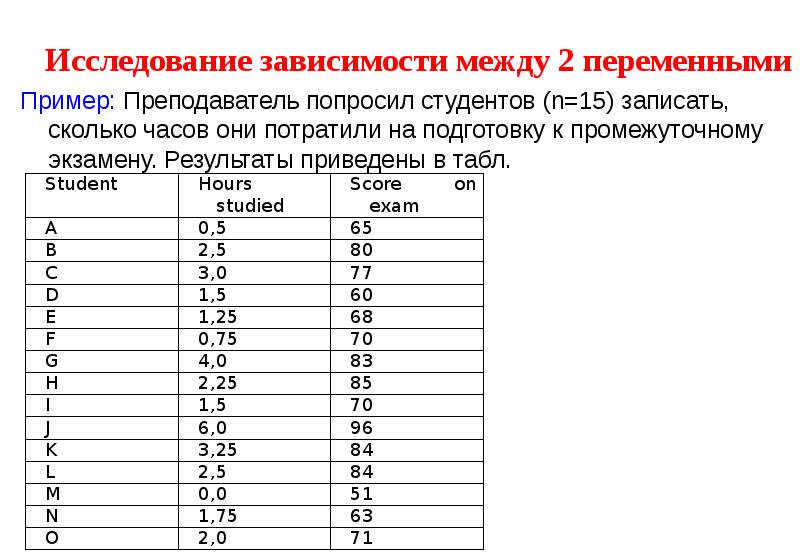
- 8. Исследование зависимости между 2 переменными Исследование зависимости между 2 переменными
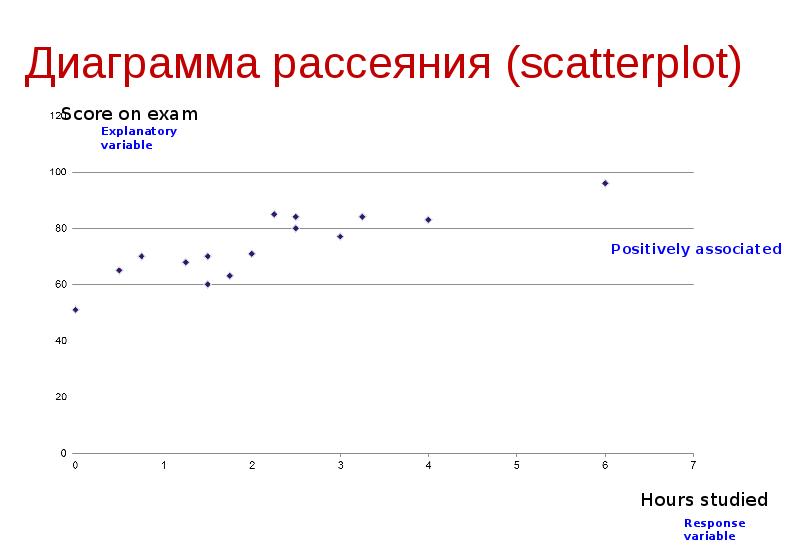
- 9. Диаграмма рассеяния (scatterplot)
- 10. «Существует ли зависимость между доходом семьи и ее расходами на питание?»
- 11. Характеристики статистической связи, рассматриваемые в корреляционном анализе используются в качестве «входной»
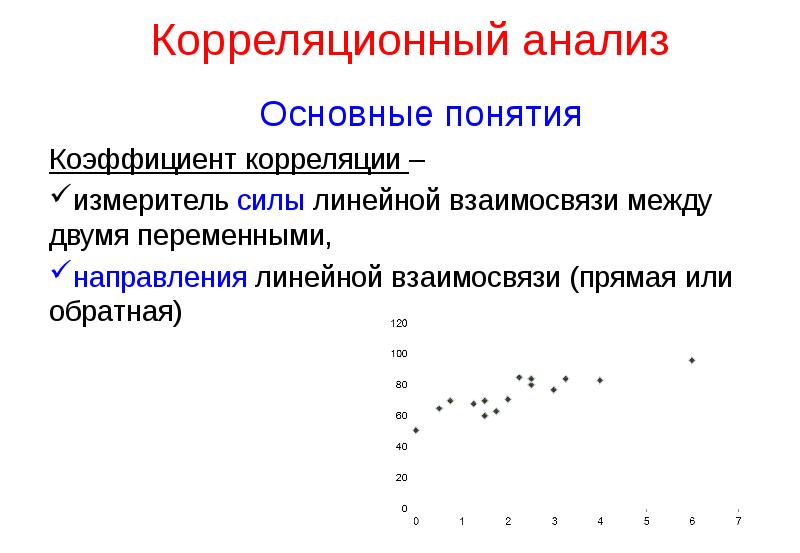
- 12. Корреляционный анализ Основные понятия Коэффициент корреляции – измеритель силы линейной
- 13. Корреляционный анализ Основные понятия Случайные величины X и Y могут
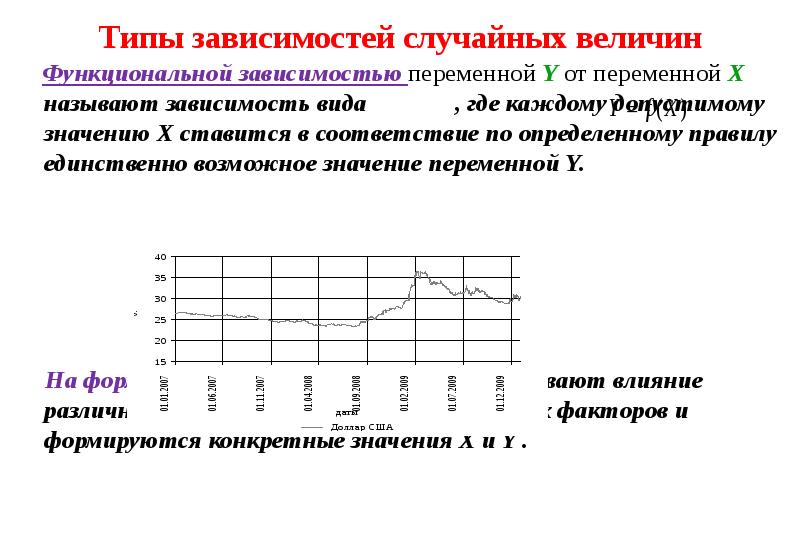
- 14. Типы зависимостей случайных величин Функциональной зависимостью переменной Y от переменной
- 15. Типы зависимостей случайных величин Пример: Допустим, что на X и
- 16. Типы зависимостей случайных величин Пример: Допустим, что на X и
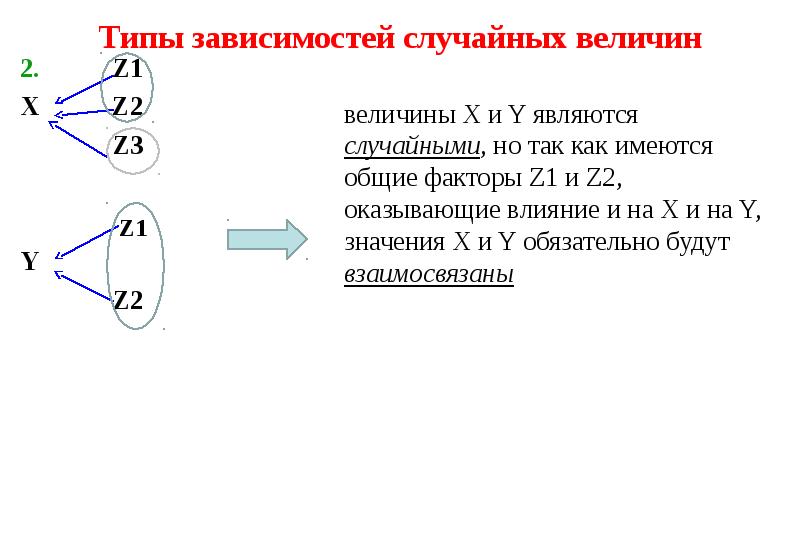
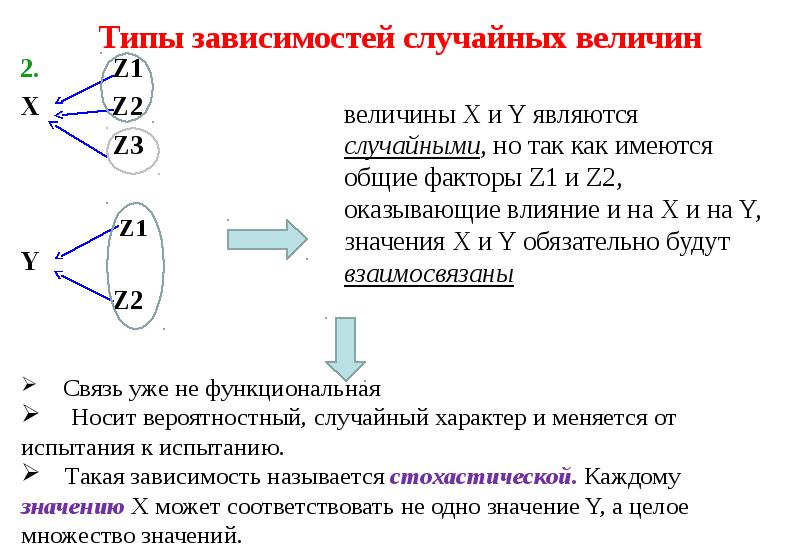
- 17. Типы зависимостей случайных величин 2. Z1 X
- 18. Типы зависимостей случайных величин 2. Z1 X
- 19. Типы зависимостей случайных величин у
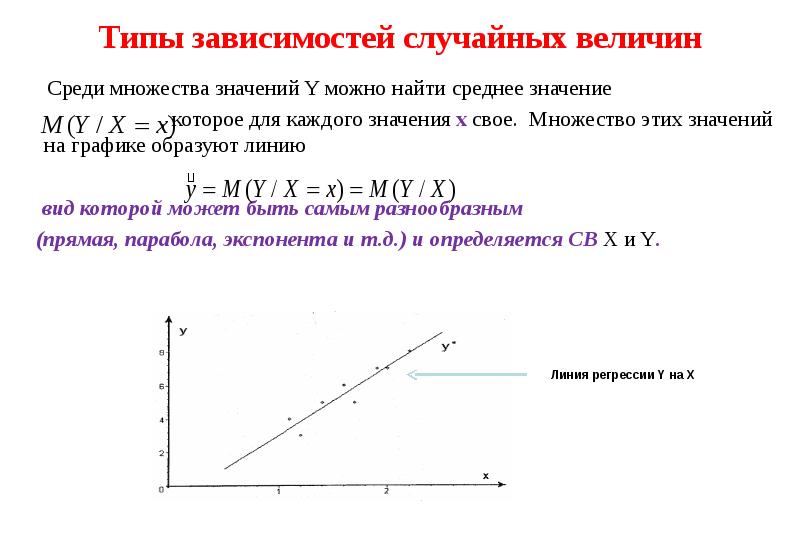
- 20. Типы зависимостей случайных величин Среди множества значений Y можно найти
- 21. Типы зависимостей случайных величин Если изменение одной из СВ приводит
- 22. Исследование зависимости между 2 переменными Исследование зависимости между 2 переменными
- 23. Линейный коэффициент корреляции Двумерная корреляционная модель Исходной для анализа является матрица
- 24. Корреляционный анализ Двумерная корреляционная модель Двумерная корреляционная модель определяется
- 25. Коэффициенты корреляции Парный коэффициент корреляции характеризует тесноту линейной взаимосвязи
- 26. Корреляционный анализ Точечные оценки параметров двумерной корреляционной модели
- 27. Диаграмма рассеяния Диаграмма рассеяния На практике изучение зависимости между
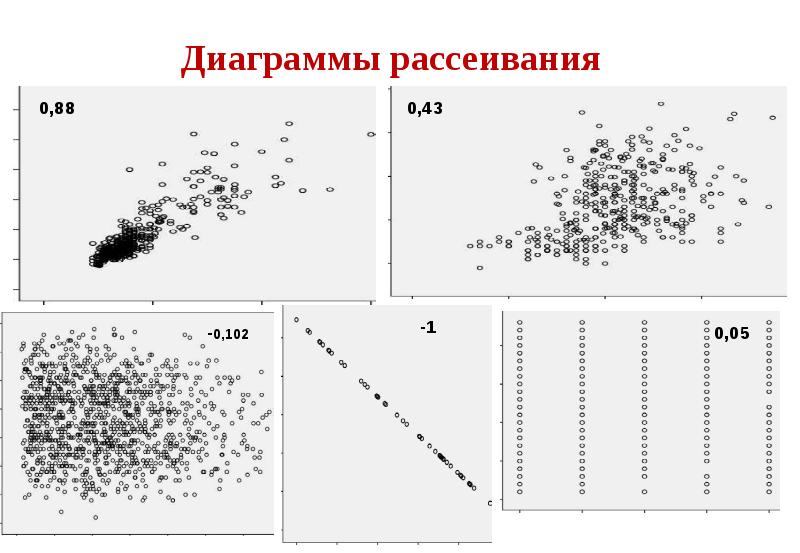
- 28. Диаграммы рассеивания
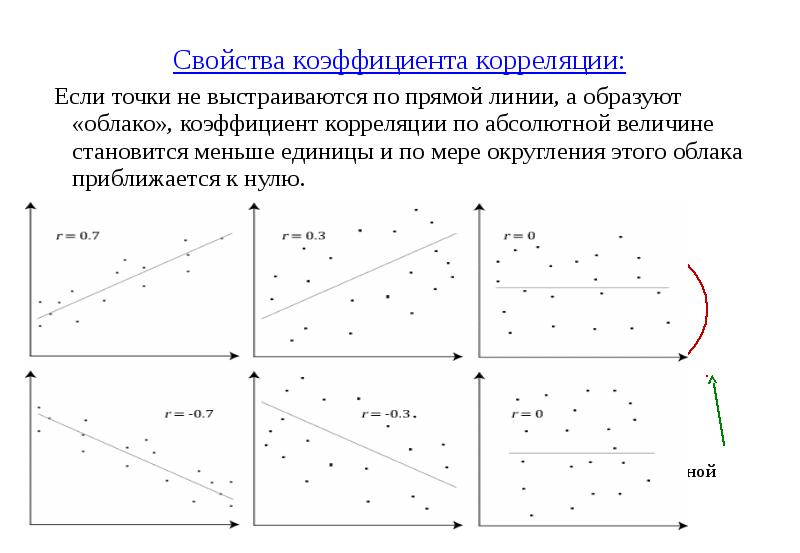
- 30. Свойства коэффициента корреляции: Если точки не выстраиваются по прямой линии,
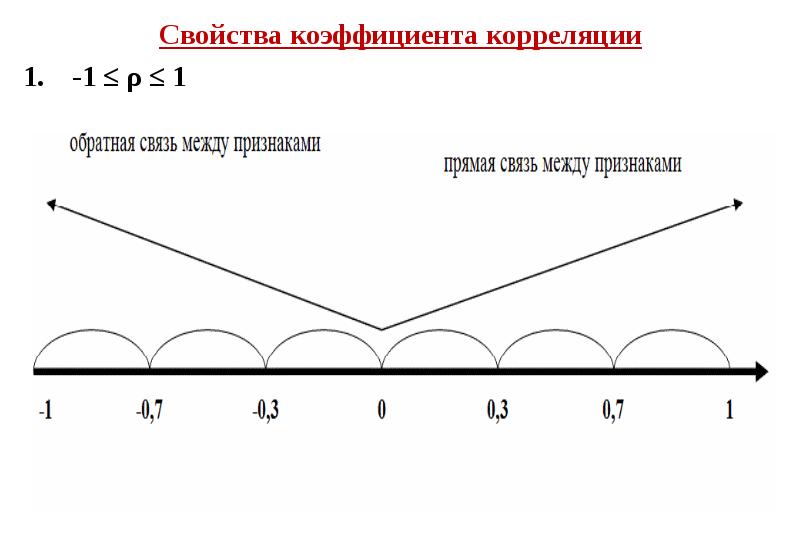
- 31. Свойства коэффициента корреляции Свойства коэффициента корреляции -1 ≤ ρ ≤ 1
- 32. Свойства коэффициента корреляции Свойства коэффициента корреляции 2. Если случайные величины
- 33. Свойства коэффициента корреляции Свойства коэффициента корреляции 2. Из условия
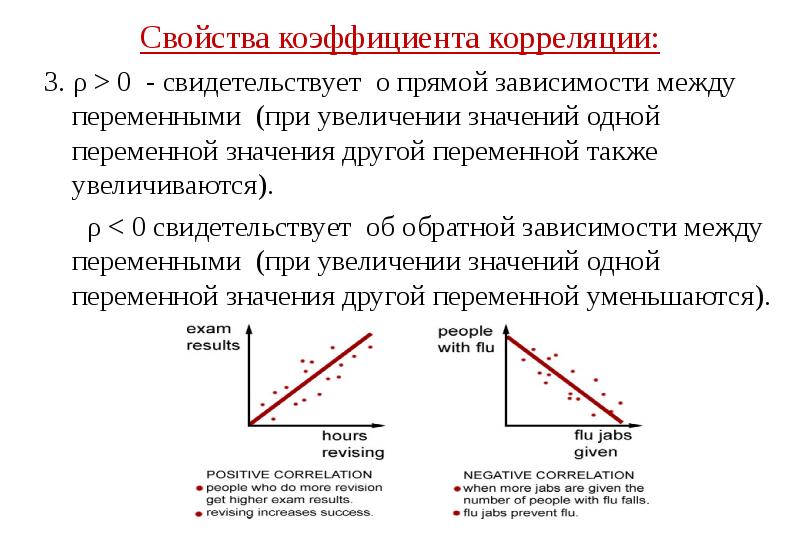
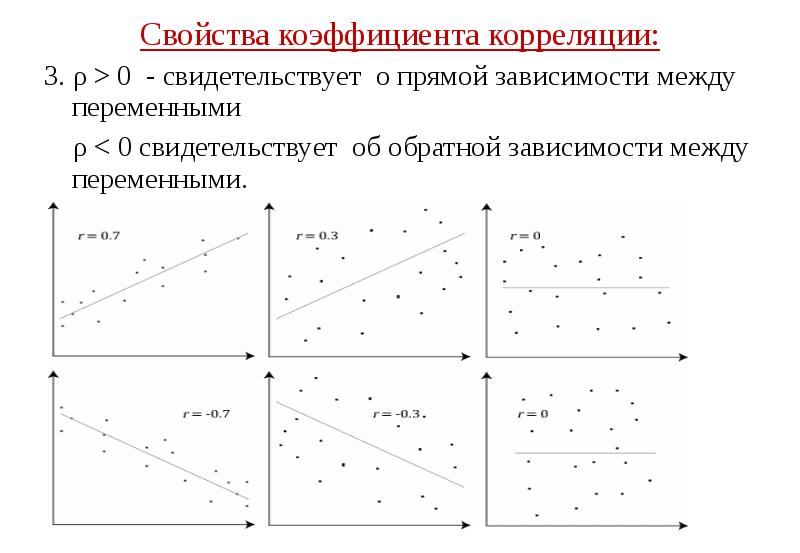
- 34. Свойства коэффициента корреляции: Свойства коэффициента корреляции: 3. ρ > 0
- 35. Свойства коэффициента корреляции: Свойства коэффициента корреляции: 3. ρ > 0
- 36. Свойства коэффициента корреляции Свойства коэффициента корреляции 45. Сила корреляционной связи не
- 37. Свойства коэффициента корреляции Свойства коэффициента корреляции Пример
- 38. Свойства коэффициента корреляции Свойства коэффициента корреляции 5. Неважно, какую переменную мы
- 39. Свойства коэффициента корреляции Свойства коэффициента корреляции 7. Коэффициент корреляции не имеет
- 40. Свойства коэффициента корреляции Свойства коэффициента корреляции 8. Если все значения переменных
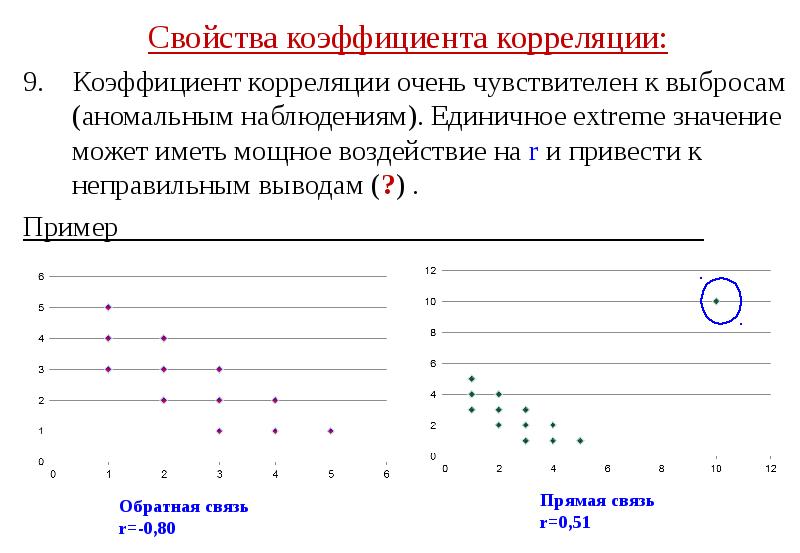
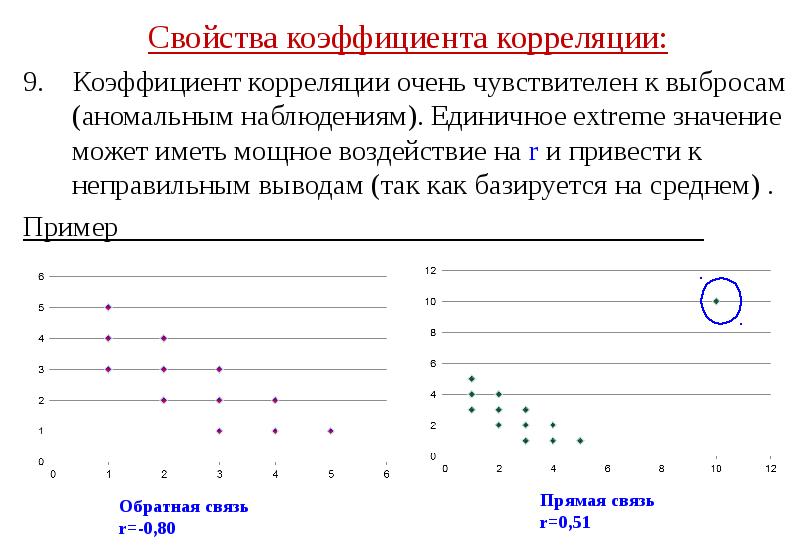
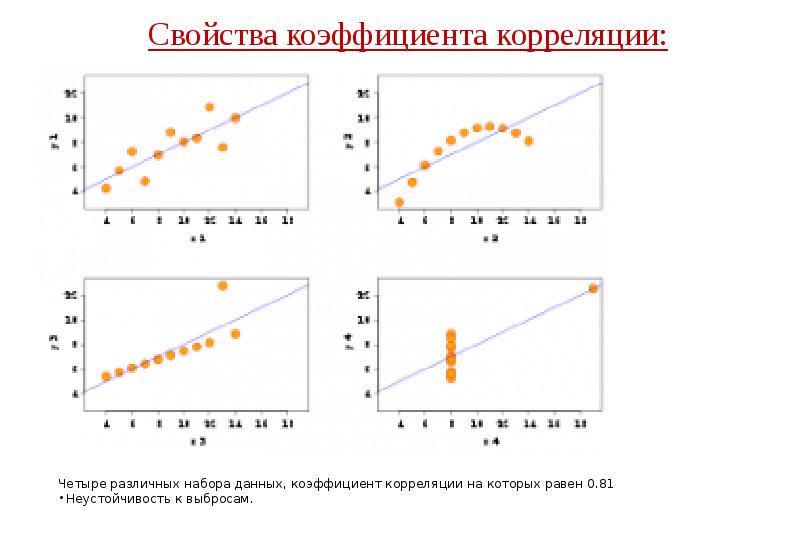
- 41. Свойства коэффициента корреляции: Свойства коэффициента корреляции: 9. Коэффициент корреляции очень чувствителен
- 42. Свойства коэффициента корреляции: Свойства коэффициента корреляции: 9. Коэффициент корреляции очень чувствителен
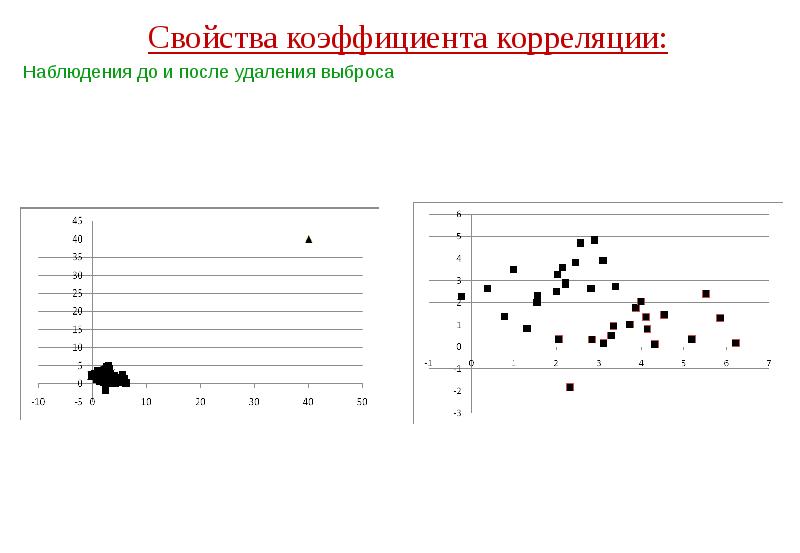
- 43. Свойства коэффициента корреляции: Свойства коэффициента корреляции: Наблюдения до и после удаления
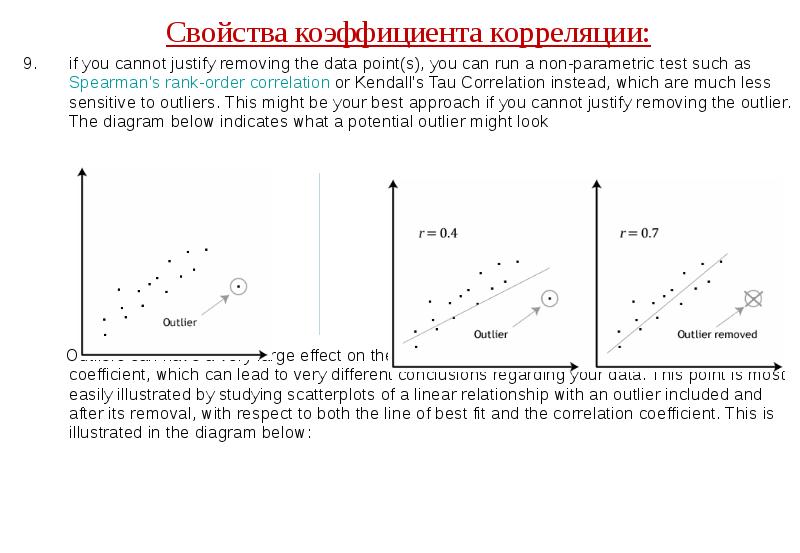
- 44. Свойства коэффициента корреляции: Свойства коэффициента корреляции: if you cannot justify removing
- 45. Свойства коэффициента корреляции: Свойства коэффициента корреляции: if you cannot justify removing
- 46. Свойства коэффициента корреляции: Свойства коэффициента корреляции: if you cannot justify removing
- 47. Свойства коэффициента корреляции: Свойства коэффициента корреляции:
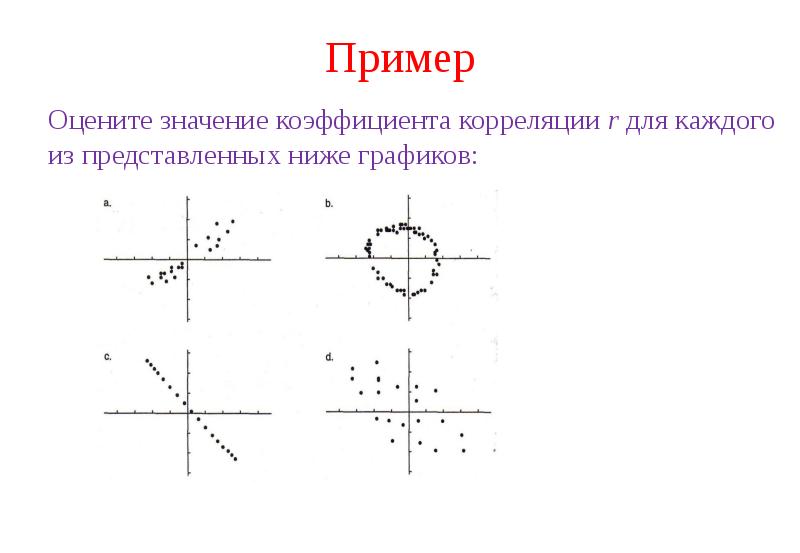
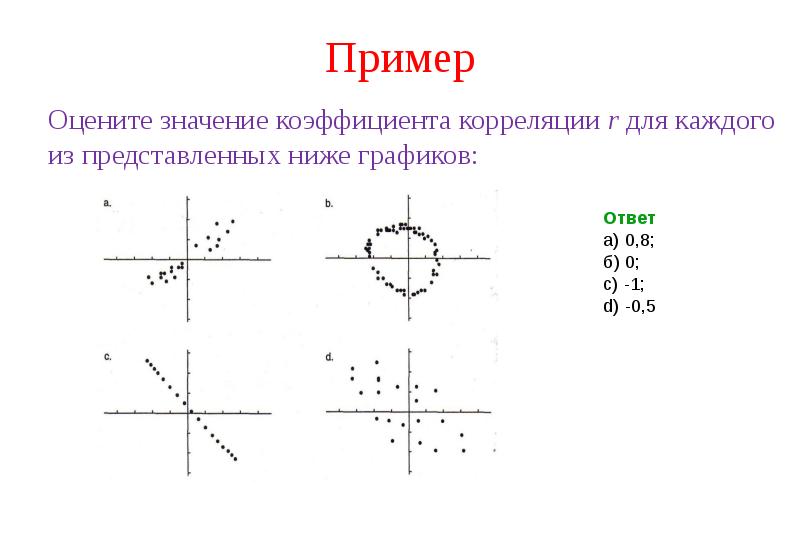
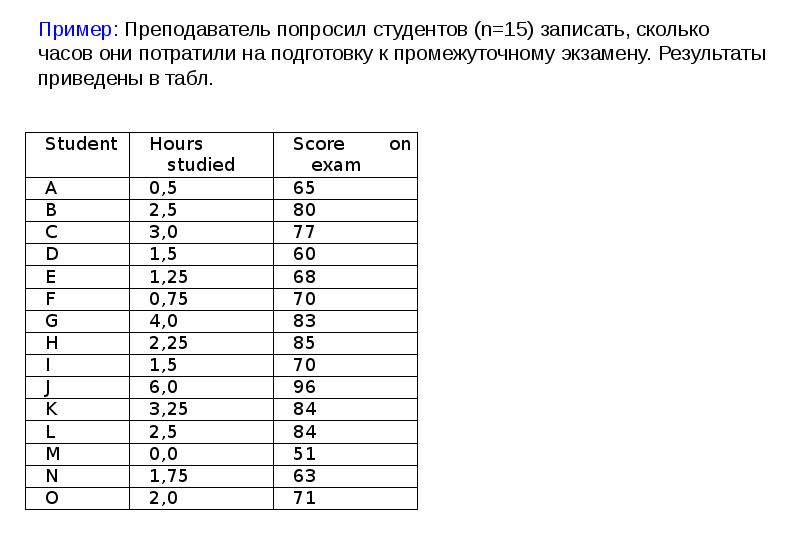
- 48. Пример Оцените значение коэффициента корреляции r для каждого из представленных
- 49. Пример Оцените значение коэффициента корреляции r для каждого из представленных
- 50. Проверка значимости коэффициента корреляции Значимость парных коэффициентов корреляции проверяется
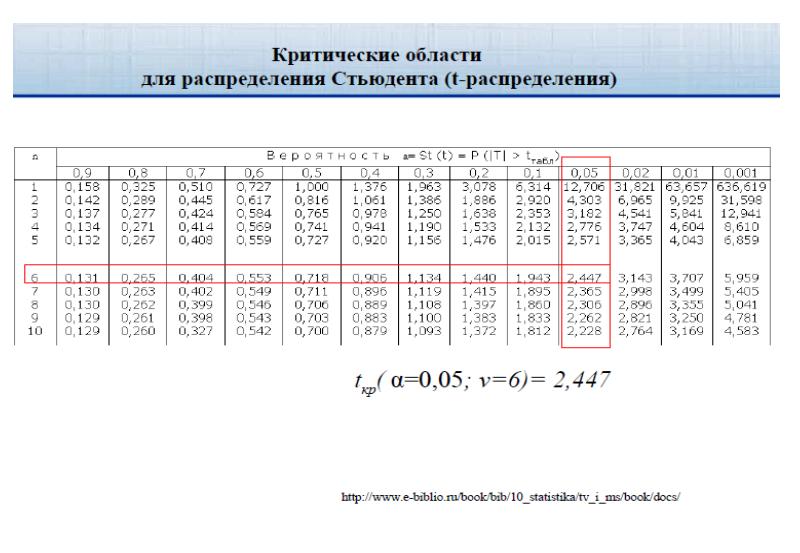
- 51. Проверка значимости коэффициента корреляции 2. Нахождение критического значения статистики
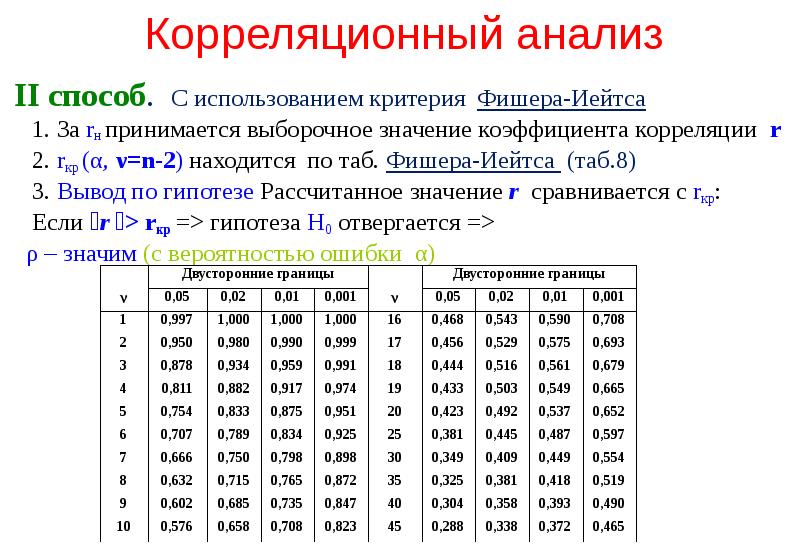
- 53. Корреляционный анализ II способ. С использованием критерия Фишера-Иейтса 1.
- 56. Проверка независимости (значимости) признаков 1. 2. 3. Вывод
- 57. Коэффициент детерминации в двумерной модели Квадрат парного коэффициент корреляции
- 58. Коэффициент детерминации в двумерной модели Квадрат парного коэффициент корреляции
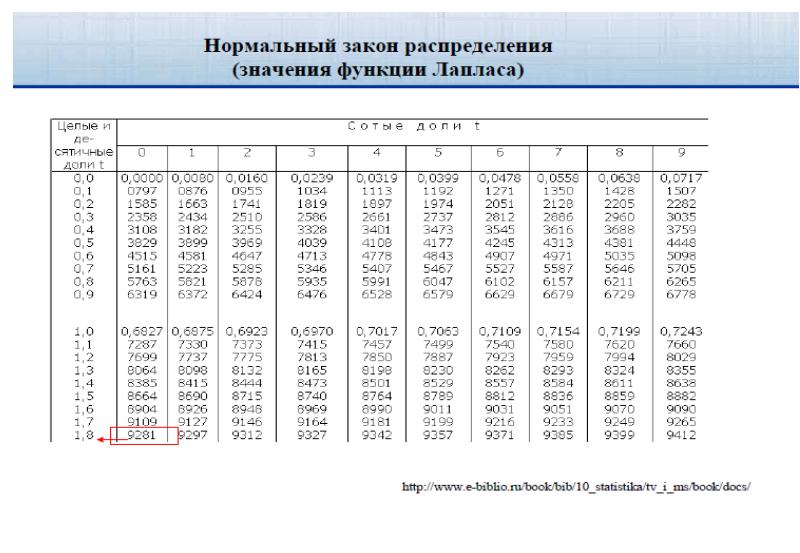
- 59. Интервальные оценки параметров связи I. Для значимых параметров связи
- 62. Интервальные оценки параметров связи 2. Обратный переход от Z к r
- 63. Трёхмерная корреляционная модель Пусть признаки X, Y, Z образуют трехмерную
- 64. Трёхмерная корреляционная модель Пусть признаки X, Y, Z образуют трехмерную
- 65. Трёхмерная корреляционная модель Для изучения разнообразия связей между тремя случайными
- 66. Трёхмерная (многомерная) корреляционная модель Исходной для анализа является матрица: X=
- 67. Трёхмерная (многомерная) корреляционная модель Парный коэффициент корреляции, например,
- 68. Матрица парных коэффициентов корреляции R =
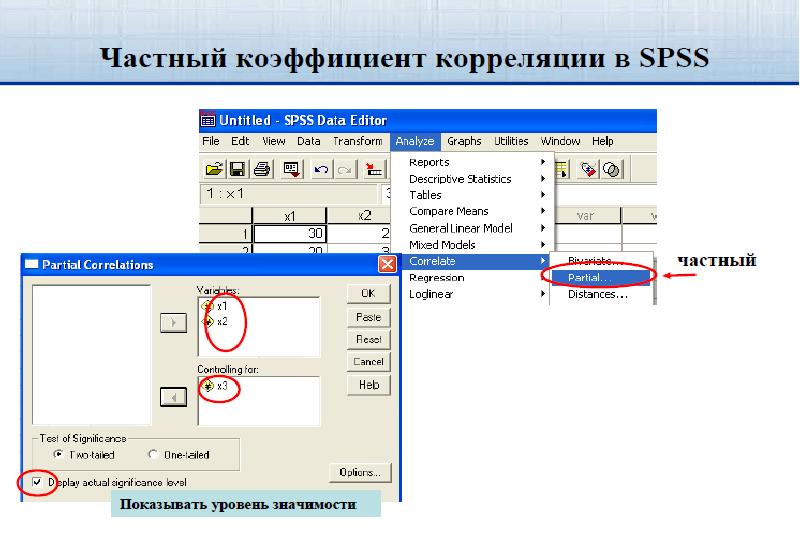
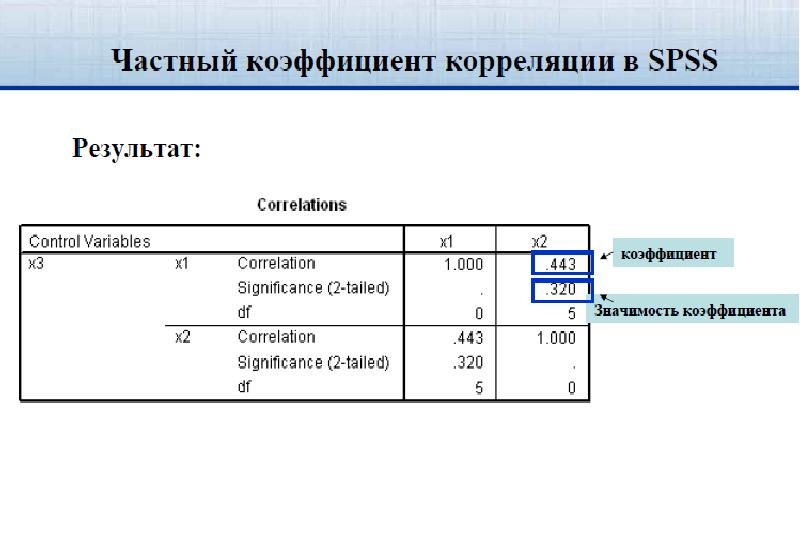
- 69. Трёхмерная корреляционная модель Частный коэффициент корреляции, например, ρxy/z характеризует тесноту связи
- 70. Трёхмерная корреляционная модель Частный коэффициент корреляции обладает всеми свойствами парного
- 71. Трёхмерная корреляционная модель Частный коэффициент корреляции например, Точечная оценка
- 72. Матрица частных коэффициентов корреляции
- 74. Трёхмерная корреляционная модель Проверка значимости парного и частного КК
- 75. Трёхмерная корреляционная модель Интервальная оценка для значимого парного
- 76. Трёхмерная корреляционная модель Множественный коэффициент корреляции Множественный коэффициент корреляции в
- 77. Трёхмерная корреляционная модель Множественный коэффициент корреляции Точечная оценка множественного
- 78. Коэффициент детерминации Квадрат множественного коэффициент корреляции
- 79. Многомерная корреляционная модель Многомерная корреляционная модель Множественный коэффициент
- 80. Множественный коэффициент корреляции и его свойства 1. Множественный коэффициент корреляции изменяется
- 81. Множественный коэффициент корреляции и его свойства 1. Множественный коэффициент корреляции изменяется
- 82. Множественный коэффициент корреляции и его свойства 3. Максимальное значение
- 83. Свойства множественного коэффициента корреляции 4. Множественный коэффициент корреляции превышает любой парный
- 84. Свойства множественного коэффициента корреляции 5. Присоединение любой новой предсказывающей переменной не
- 85. Коэффициент детерминации Наибольшему множественному коэффициенту детерминации соответствуют большие частные коэффициенты
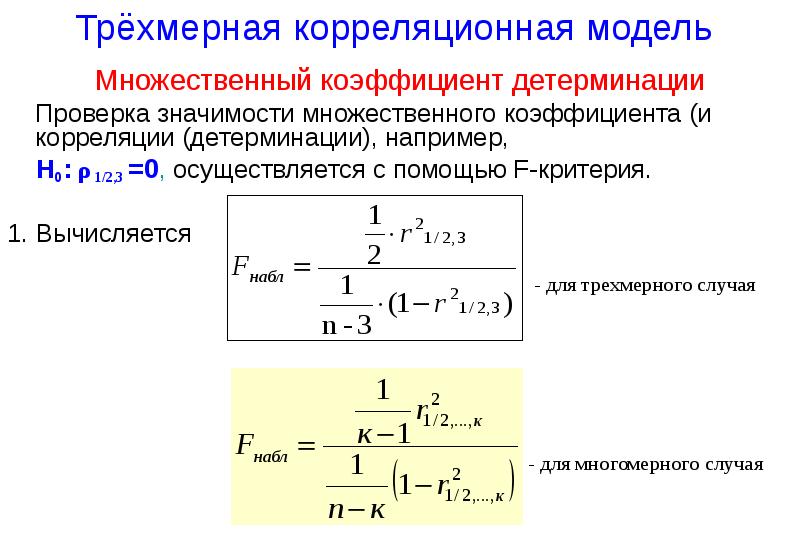
- 86. Трёхмерная корреляционная модель Множественный коэффициент детерминации Проверка значимости множественного коэффициента (и
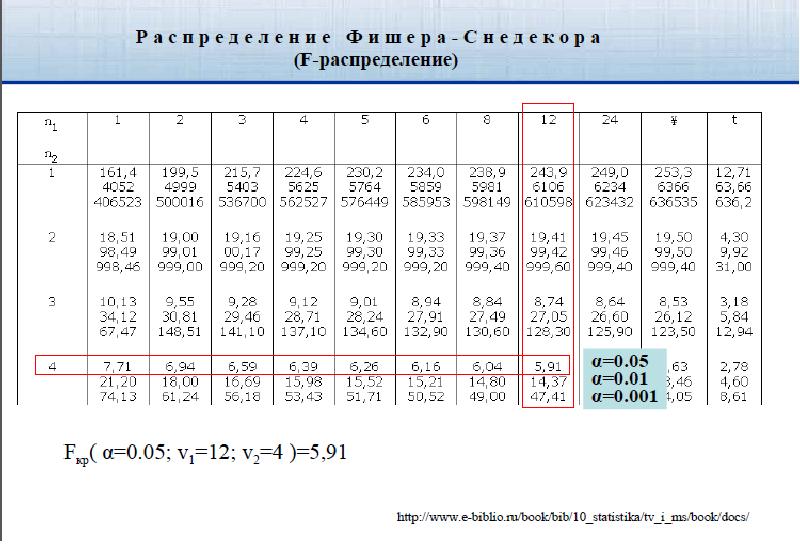
- 87. Трёхмерная корреляционная модель Множественный коэффициент детерминации По таблице F-распределения Фишера-Снедекора
- 89. Корреляционный анализ
- 91. Число наблюдений достаточно велико Если число наблюдений достаточно велико и
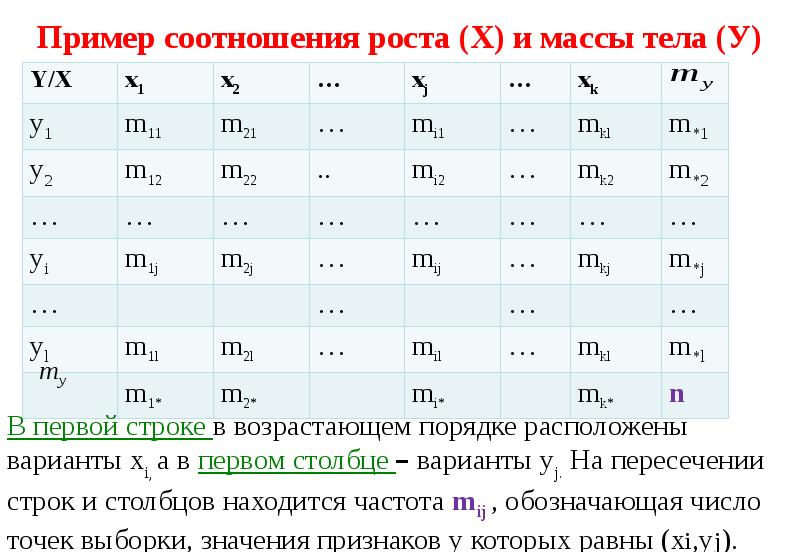
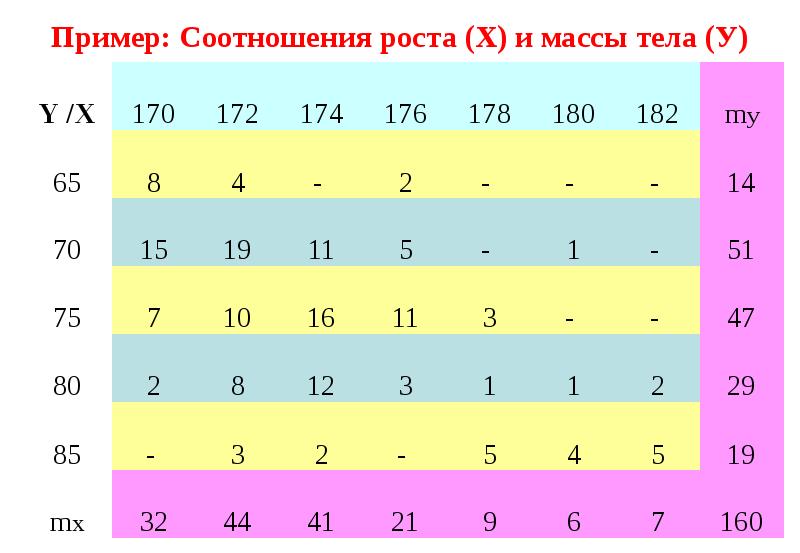
- 92. Пример соотношения роста (Х) и массы тела (У)
- 93. Корреляционная таблица Некоторые mij=0. В последней строке
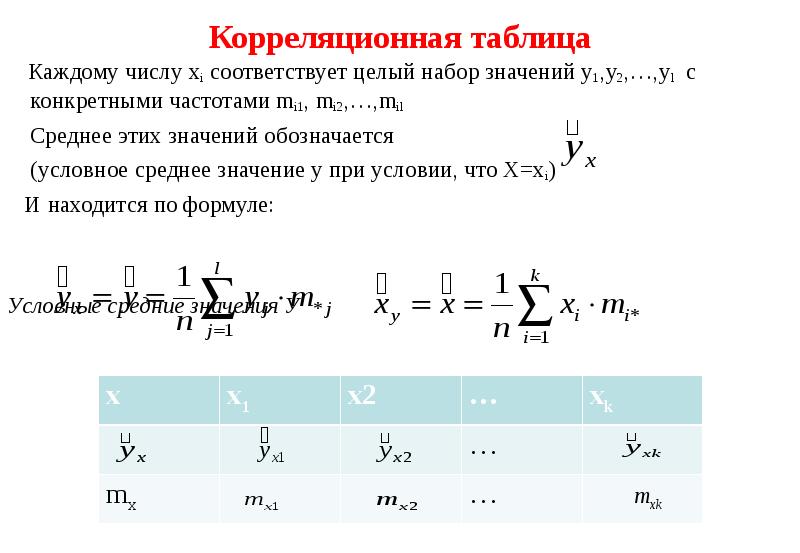
- 94. Корреляционная таблица Каждому числу xi соответствует целый набор значений y1,y2,…,yl
- 95. Пример: Соотношения роста (Х) и массы тела (У)
- 96. Решение Выборочный коэффициент корреляции в случае сгруппированных данных по корреляционной
- 97. Решение Суммирование распространяется в знаменателе на все возможные х
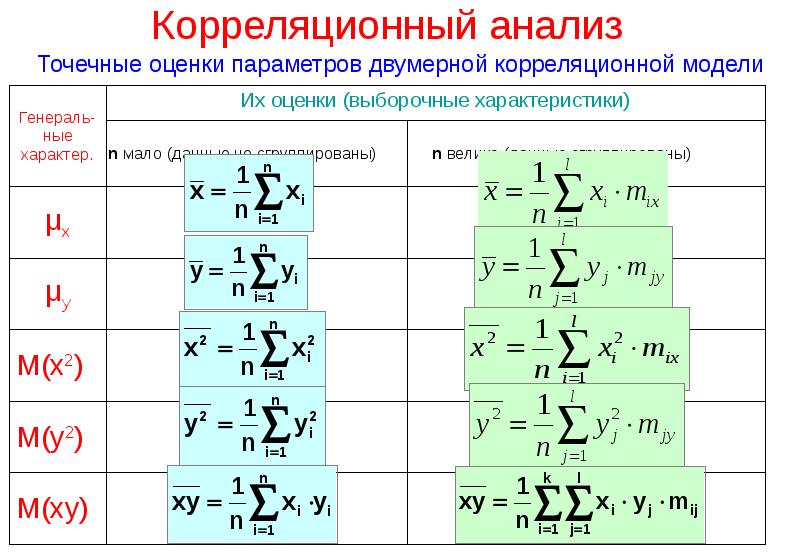
- 98. Корреляционный анализ Точечные оценки параметров двумерной корреляционной модели
- 99. Проверка независимости (значимости) признаков Значимость парных коэффициентов корреляции можно проверить
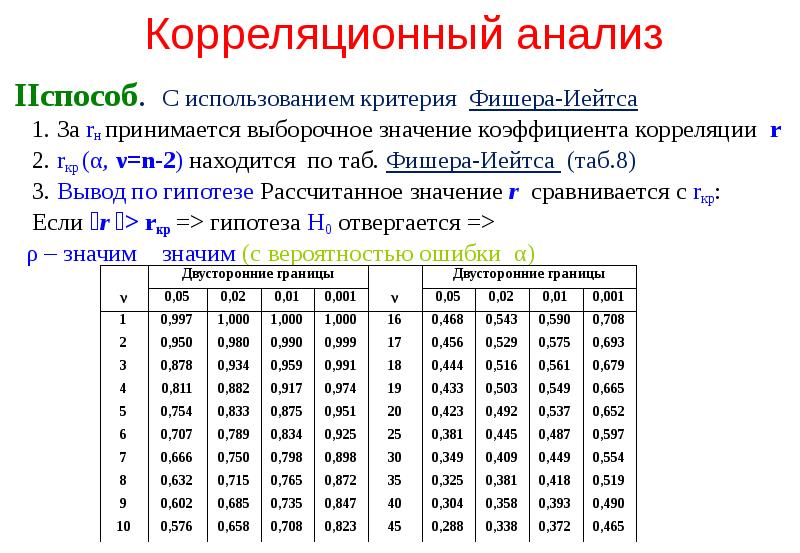
- 100. Корреляционный анализ IIспособ. С использованием критерия Фишера-Иейтса 1. За
- 101. Интервальные оценки параметров связи Для значимых параметров связи (парных
- 102. Интервальные оценки параметров связи 2. Обратный переход от Z к r
- 103. Корреляционный анализ
- 104. Коэффициент детерминации
- 105. Матрица парных коэффициентов корреляции (многомерный случай) R =
- 106. Корреляционный анализ В двумерном корреляционном анализе обычно строят корреляционную
- 107. Корреляционный анализ При небольших объемах выборки часто используют более предпочтительные оценки
- 108. Корреляционный анализ Уравнения линий регрессии Если наблюдаемые значения
- 109. Корреляционный анализ
- 110. Корреляционный анализ II. Интервальные оценки генеральных коэффициентов корреляции и регрессии
- 111. Двумерная корреляционная модель Остаточная дисперсия Выборочная дисперсия переменной Y может быть
- 112. Корреляционный анализ Точечные оценки параметров двумерной корреляционной модели
- 113. Трёхмерная корреляционная модель условные дисперсии
- 114. Трёхмерная корреляционная модель Множественный коэффициент детерминации Проверка значимости множественного коэффициента (и
- 115. Трёхмерная корреляционная модель Множественный коэффициент детерминации По таблице F-распределения Фишера-Снедекора
- 116. Скачать презентацию



















































































Слайды и текст этой презентации
Похожие презентации





























