Отношения, графы, деревья презентация
Содержание
- 2. Определение. Пусть а и b — объекты. Определение. Пусть а
- 3. Отношения Определение. Пусть А и В —множества. Отношением из А
- 4. Свойства отношений Определение. Пусть A—множество и R — отношение на A.
- 5. Графы Определение. Неупорядоченный граф G — это пара (А, R),
- 6. Пара (а, b)R называется дугой (или ребром) графа G. Пара
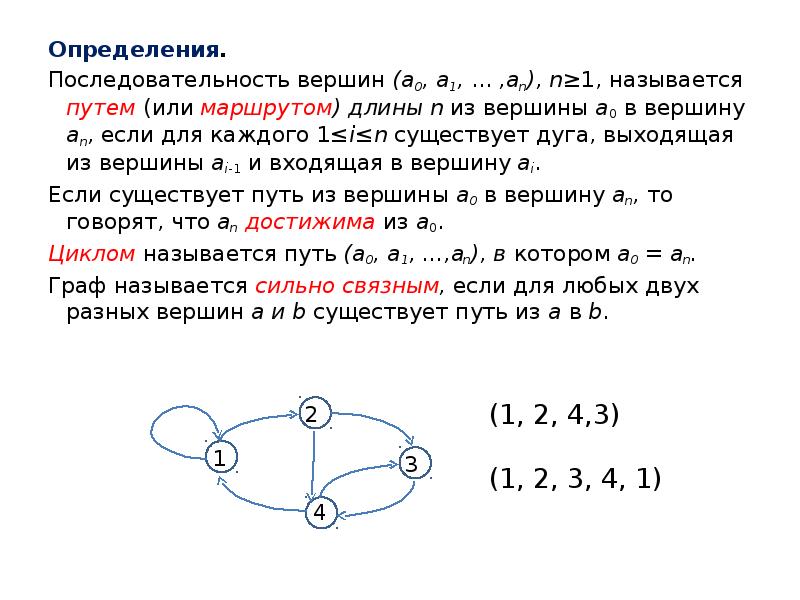
- 7. Определения. Определения. Последовательность вершин (а0, а1, ... ,аn), n≥1,
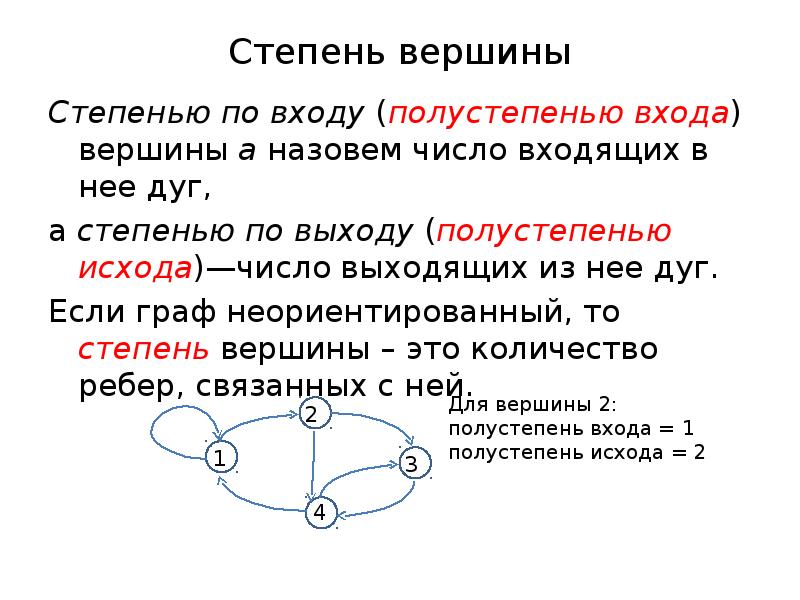
- 8. Степень вершины Степенью по входу (полустепенью входа) вершины а назовем число
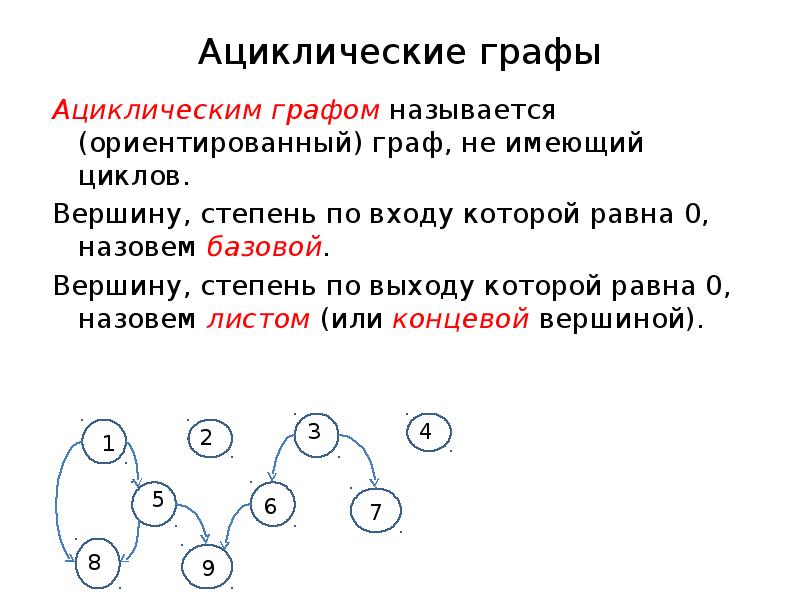
- 9. Ациклические графы Ациклическим графом называется (ориентированный) граф, не имеющий циклов. Вершину,
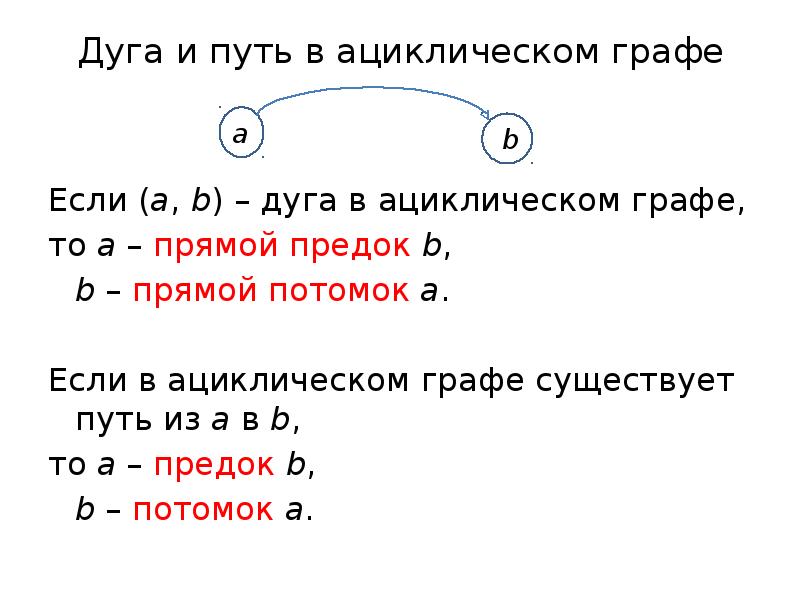
- 10. Дуга и путь в ациклическом графе Если (a, b) – дуга
- 11. Дерево (частный вид ациклического графа) Определение. (Ориентированным) деревом Т называется (ориентированный)
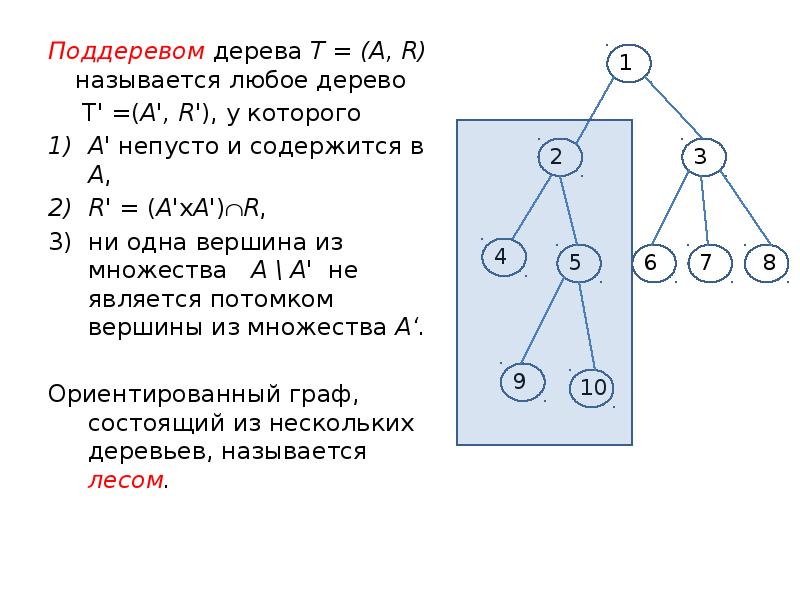
- 12. Поддеревом дерева Т = (А, R) называется любое дерево Поддеревом дерева
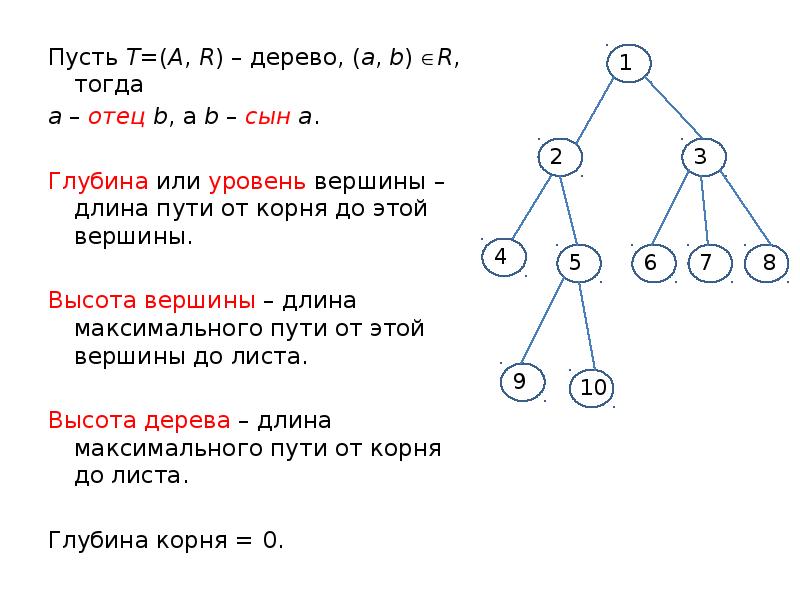
- 13. Пусть Т=(A, R) – дерево, (a, b) R, тогда Пусть Т=(A,
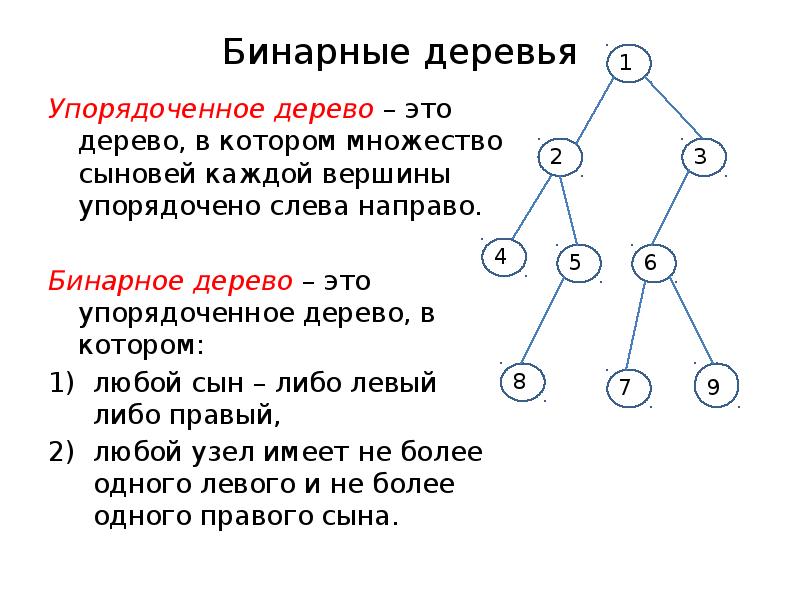
- 14. Бинарные деревья Упорядоченное дерево – это дерево, в котором множество сыновей
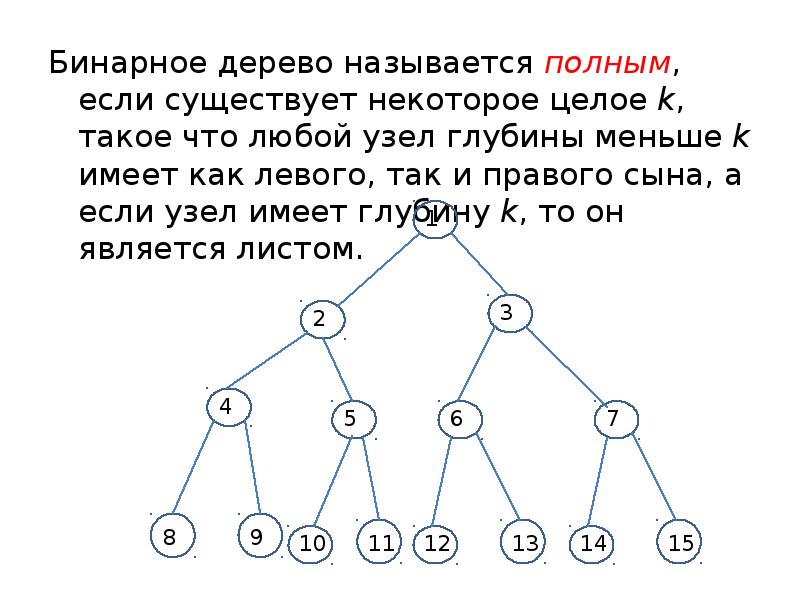
- 15. Бинарное дерево называется полным, если существует некоторое целое k, такое что
- 16. Представление полных бинарных деревьев с помощью массива Пусть T[2k-1] – массив
- 17. Скачать презентацию







![Представление полных бинарных деревьев с помощью массива
Пусть T[2k-1] – массив Представление полных бинарных деревьев с помощью массива
Пусть T[2k-1] – массив](/documents_3/d79be698ac7a74ae3d5439dd923a818c/img15.jpg)
Слайды и текст этой презентации
Похожие презентации





























