Потенциальная яма в импульсном представлении презентация

1.5. Потенциальная яма в импульсном представлении Импульсное представление. Распределение по импульсам. Возврат в координатное представление

Импульсное представление Спектр квантовой задачи является инвариантом, не зависящим от выбора базиса Импульсное представление – фурье-преобразование координатного пространства Базис в импульсном представлении L – ширина ямы или ширина области, в которой локализован потенциал или волновые функции частицы Формально базис при построении гамильтоновой матрицы можно представить в виде Единица означает, что соответствующая базисная функция описывает состояние частицы с импульсом k

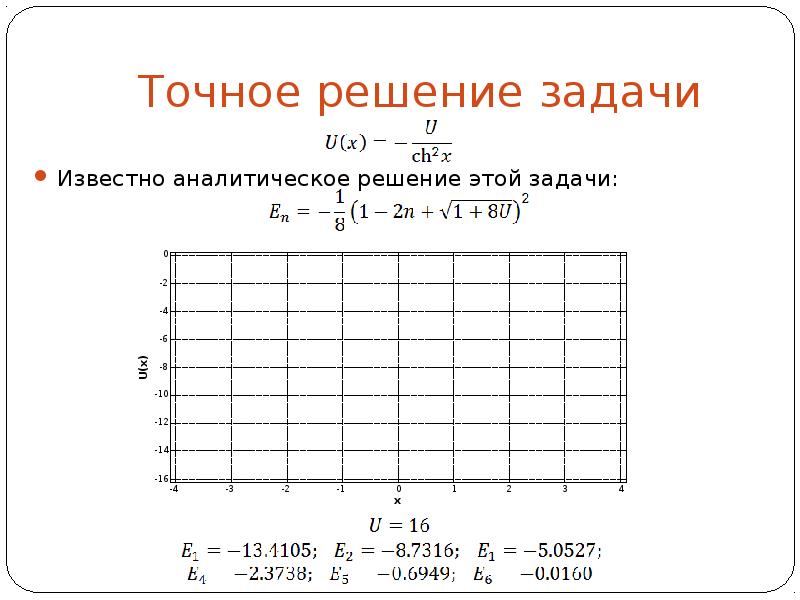
Точное решение задачи Известно аналитическое решение этой задачи:

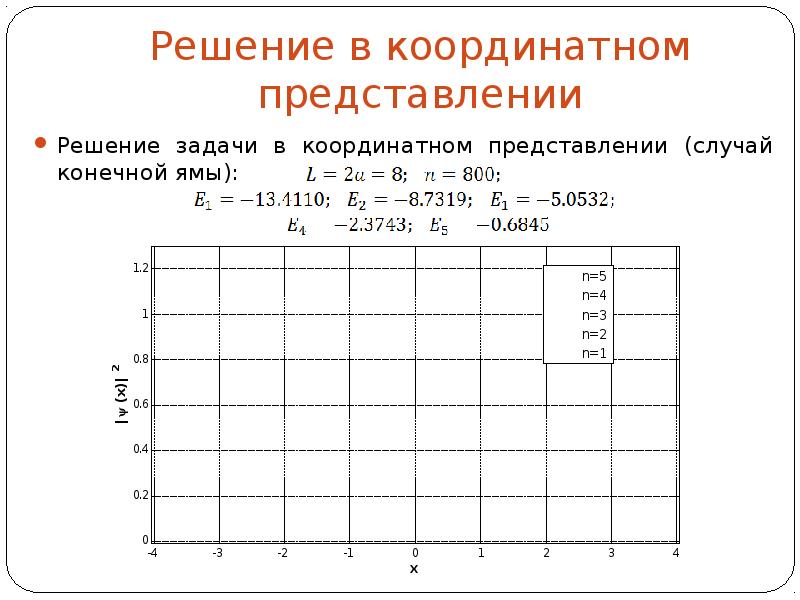
Решение в координатном представлении Решение задачи в координатном представлении (случай конечной ямы):

Решение в импульсном представлении Для решения задачи в импульсном представлении следует записать гамильтониан в терминах импульсного базиса Кинетическая энергия диагональна в импульсном представлении: Слагаемое, отвечающее потенциальной энергии частицы, недиагонально: Результат расчета практически не изменится, если последнее выражение рассчитать аналитически:

Решение в импульсном представлении Гамильтонова матрица в импульсном представлении: Матрица является плотной Результатом диагонализации будут собственные значения, являющиеся спектром системы, и собственные функции, отвечающие этим собственным значениям, которые теперь будут зависеть не от координаты, а от импульса частицы Значения импульса меняются от – π/h до π/h с шагом π/a

Распределение по импульсам Спектр системы не зависит от представления, в котором построена гамильтонова матрица. Решение задачи в импульсном представлении: Собственные функции зависят от представления, в котором построена гамильтонова матрица. После диагонализации матрицы будут получены собственные функции в импульсном представлении.

Распределение по импульсам

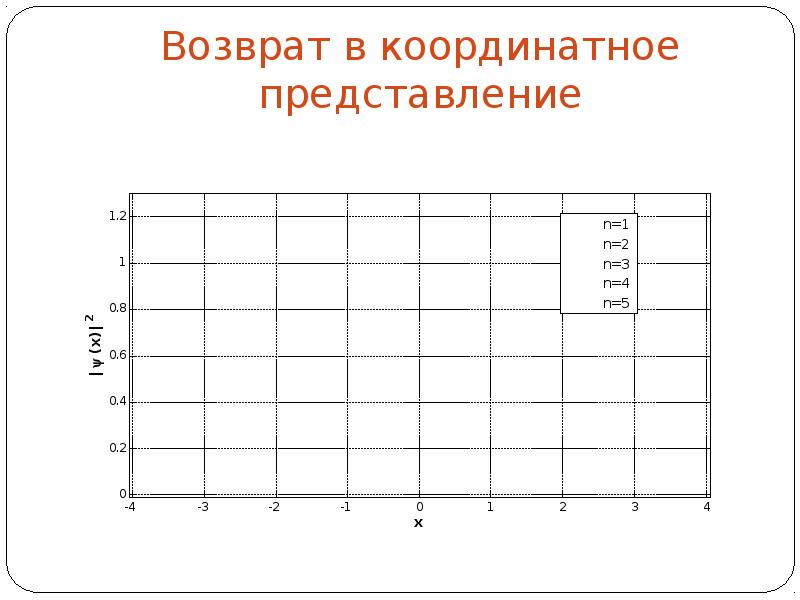
Возврат в координатное представление Чтобы получить из собственных функций в импульсном представлении собственные функции в координатном представлении, необходимо выполнить обратное фурье-преобразование: Для четных собственных функций: Для нечетных собственных функций:

Возврат в координатное представление