Распределение газовых молекул по скоростям и энергиям презентация
Содержание
- 2. 1. Скорости газовых молекул. Опыт Штерна В средине XIX века
- 3. Теоретики первыми нашли выход. Из уравнения молекулярно-кинетической теории газов известно, что
- 4. Например, при плотности азота, равной 1,25 кг/м3, при t = 0
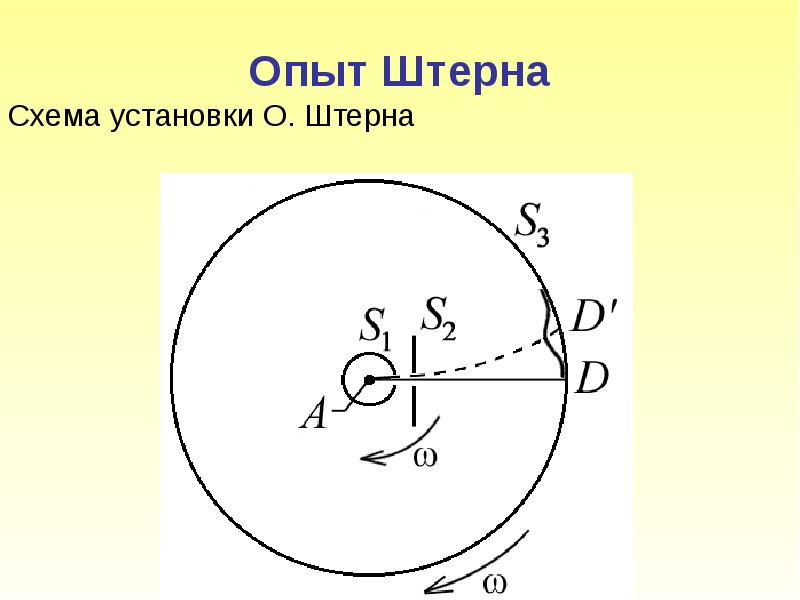
- 5. Опыт Штерна Схема установки О. Штерна
- 6. Платиновая нить А, покрытая снаружи серебром, располагается вдоль оси коаксиальных цилиндров
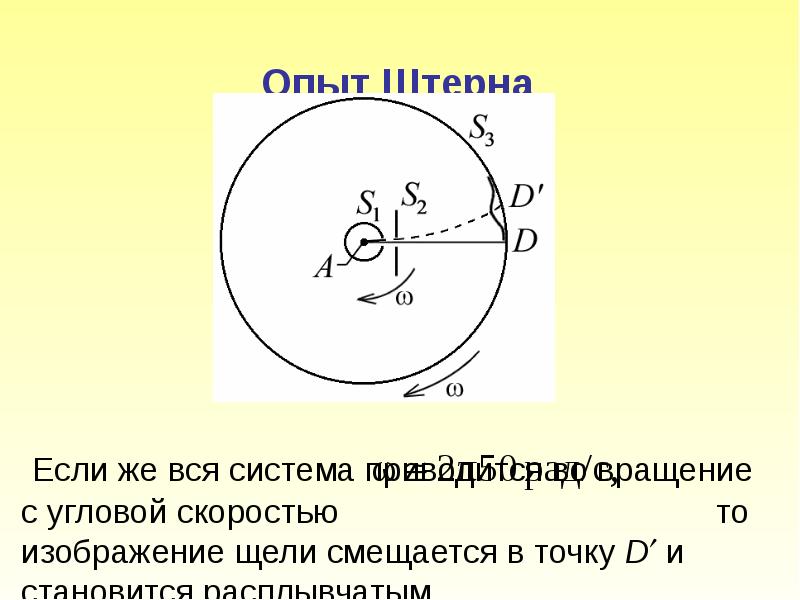
- 7. Опыт Штерна Если же вся система
- 8. Пусть l – расстояние между D и D/, измеренное вдоль поверхности
- 9. Температура нити в опытах Штерна равнялась 1200С, что соответствует среднеквадратичной скорости
- 10. Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно сталкиваясь
- 11. 2. Вероятность события. Понятие о распределении молекул газа по скоростям 2.
- 13. Математическое определение вероятности: вероятность какого-либо события – это предел, к которому
- 14. Молекулы движутся хаотически. Среди них есть и очень быстрые, и очень
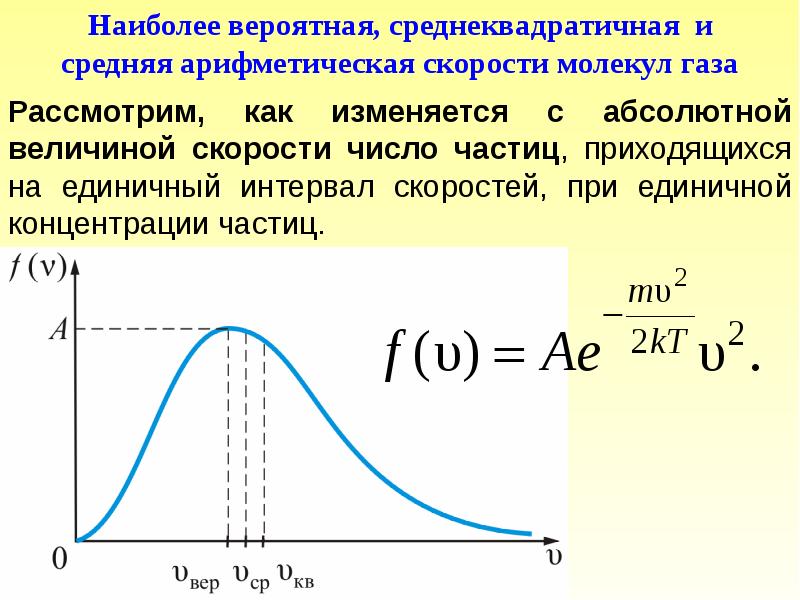
- 17. Таким образом, f(υ) – имеет смысл вероятности, то есть показывает, какова
- 18. 3. Функция распределения Максвелла 3. Функция распределения Максвелла Пусть имеется
- 20. Максвелл Джеймс Клерк (1831 – 1879) – английский физик. Работы посвящены
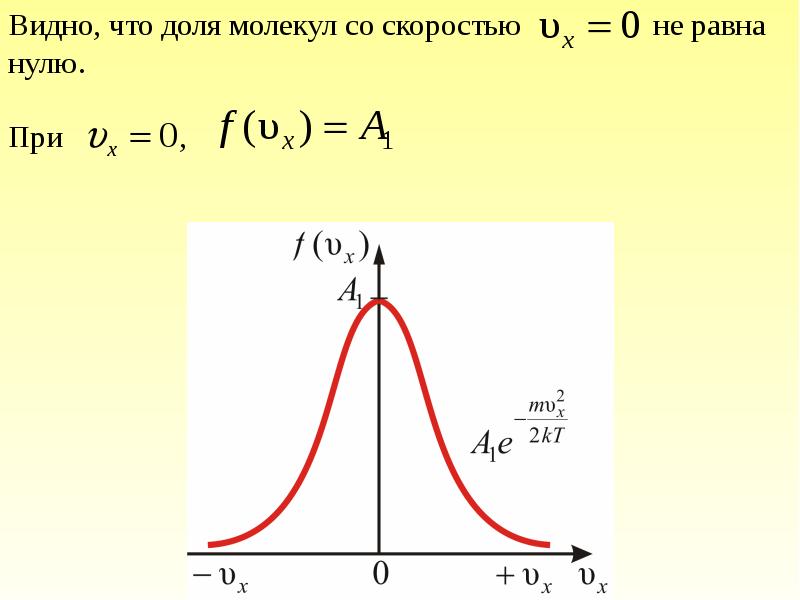
- 21. Скорость – векторная величина. Для проекции скорости на ось х (x-ой
- 23. Приведённое выражение и график справедливы для распределения молекул газа по x-ым
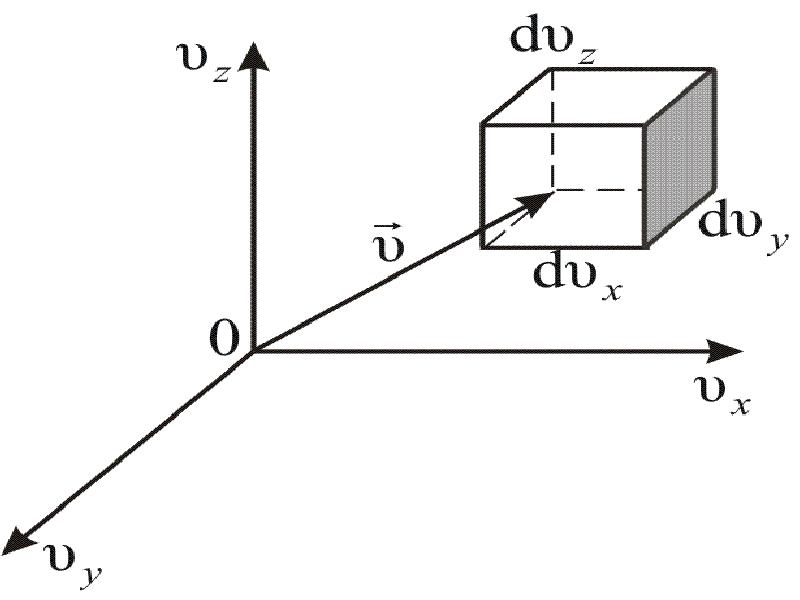
- 24. Вероятность того, что скорость молекулы одновременно удовлетворяет трём условиям: x –
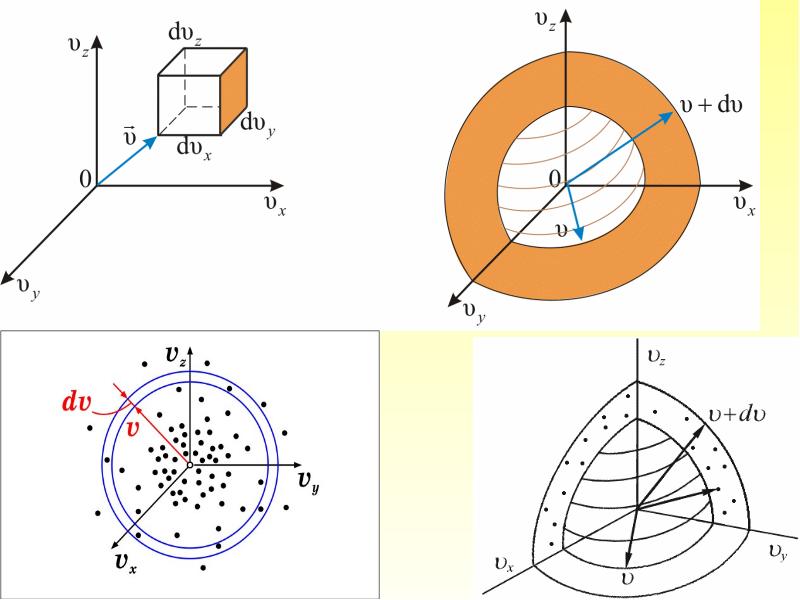
- 25. Или
- 29. Объём этого шарового слоя: Общее число молекул в слое:
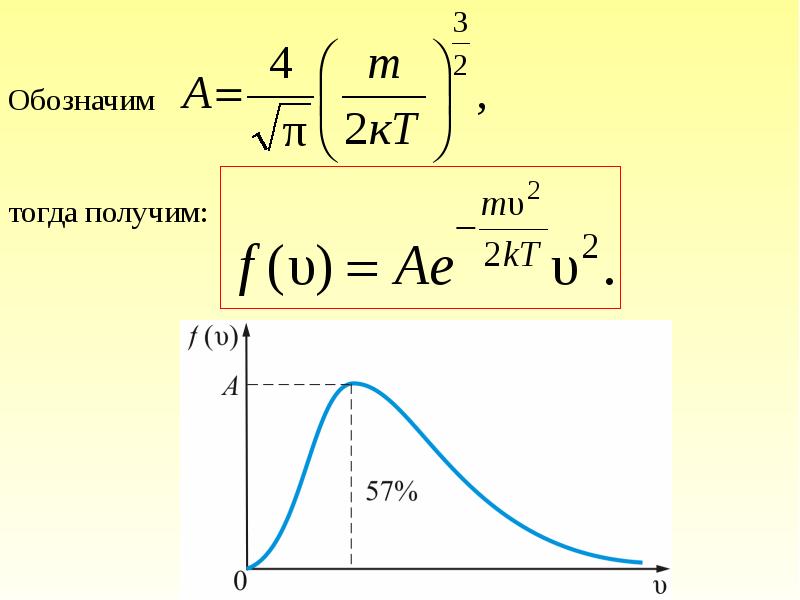
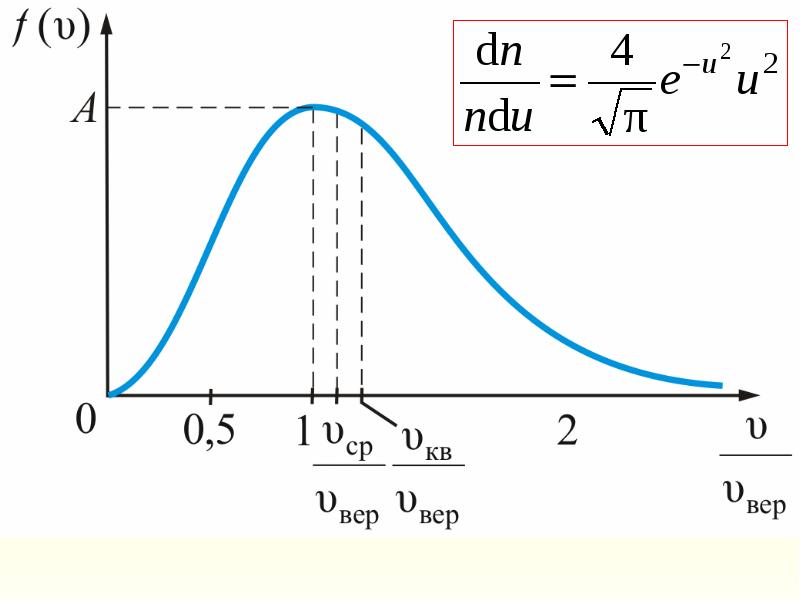
- 30. Отсюда следует закон Максвелла – распределение молекул по абсолютным значениям скоростей:
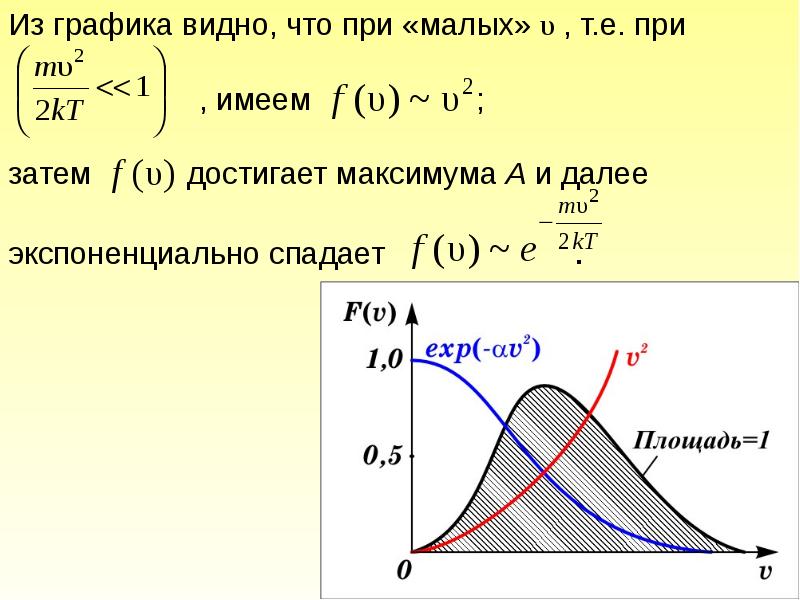
- 31. При получаем плотность вероятности, или функцию распределения молекул
- 34. Рассмотрим пределы применимости классического описания распределения частиц по скоростям.
- 35. Здесь –
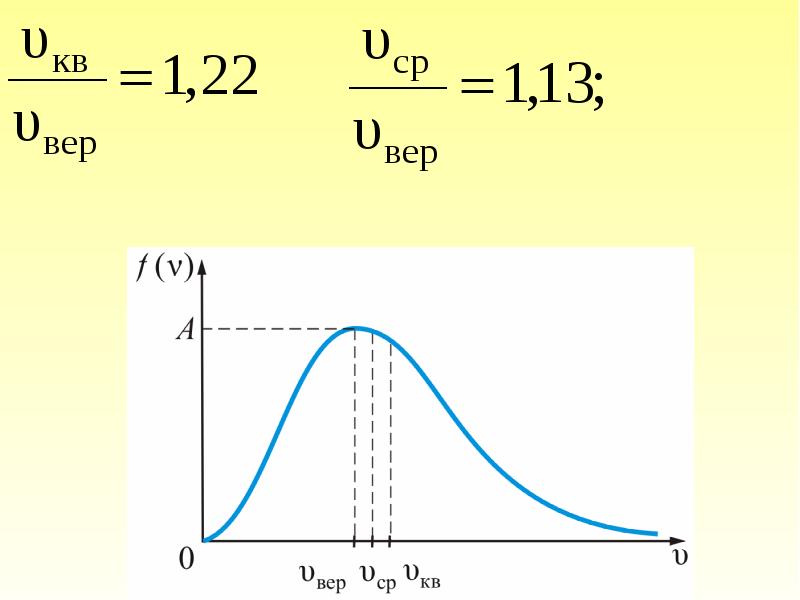
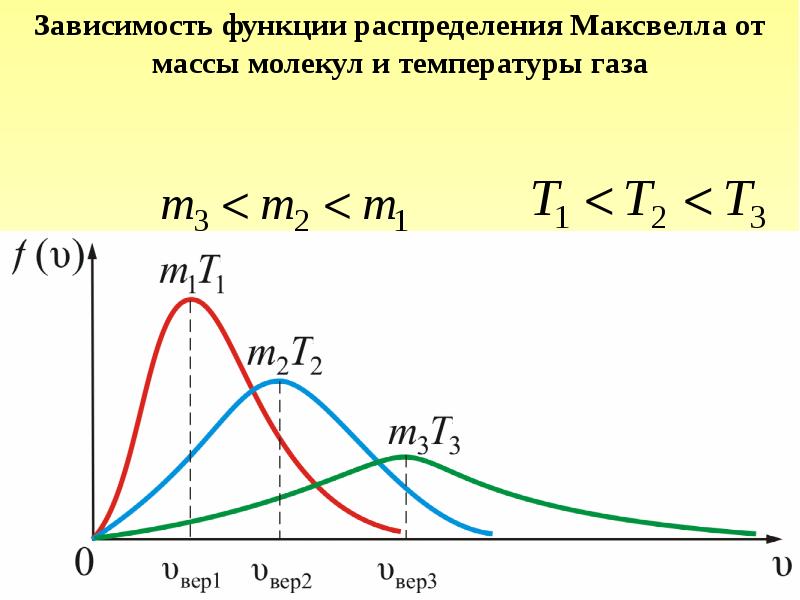
- 36. Рассмотрим, как изменяется с абсолютной величиной скорости число частиц, приходящихся на
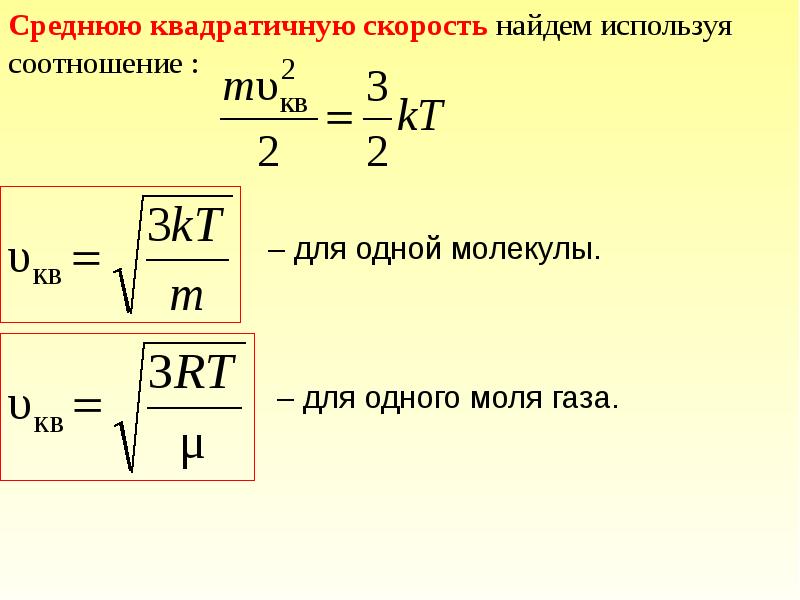
- 40. Средняя арифметическая скорость υср где
- 42. Формула Максвелла для относительных скоростей Для решения многих задач удобно использовать
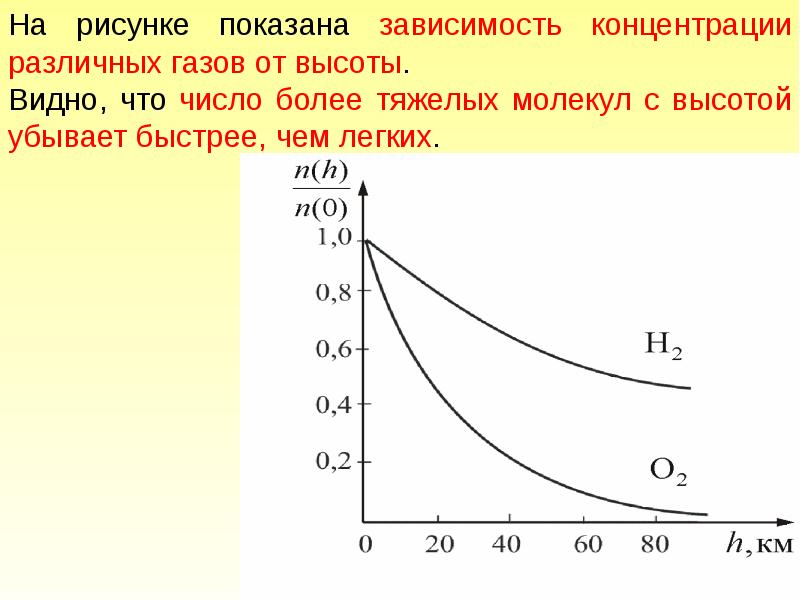
- 47. Атмосферное давление на какой-либо высоте обусловлено весом выше лежащих слоёв газа.
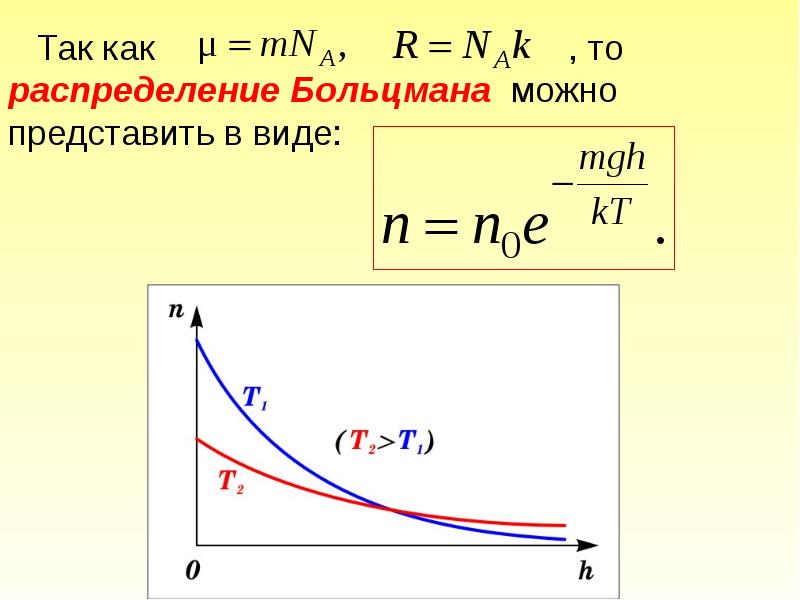
- 51. Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового
- 60. Отсюда получим функцию распределения молекул по энергиям теплового движения:
- 62. Обозначим E=U+K – полная энергия. Тогда
- 64. где Ni – число частиц, находящихся в состоянии с энергией Еi,
- 65. Тогда, окончательное выражение распределения Максвелла-Больцмана для случая дискретных значений будет иметь
- 66. Скачать презентацию



















































Слайды и текст этой презентации
Скачать презентацию на тему Распределение газовых молекул по скоростям и энергиям можно ниже:
Похожие презентации