Распределение газовых молекул по скоростям и энергиям (Тема 2) презентация
Содержание
- 2. Тема 2. РАСПРЕДЕЛЕНИЕ ГАЗОВЫХ МОЛЕКУЛ ПО СКОРОСТЯМ И ЭНЕРГИЯМ 2.1. Скорости
- 4. 2.1. Скорости газовых молекул. Опыт Штерна В средине XIX века
- 5. Теоретики первыми нашли выход. Из уравнения молекулярно-кинетической теории газов известно, что
- 6. Получена хорошая формула для расчета среднеквадратичной скорости, но масса молекулы неизвестна.
- 7. Например, при плотности азота, равной 1,25 кг/м3, при t = 0
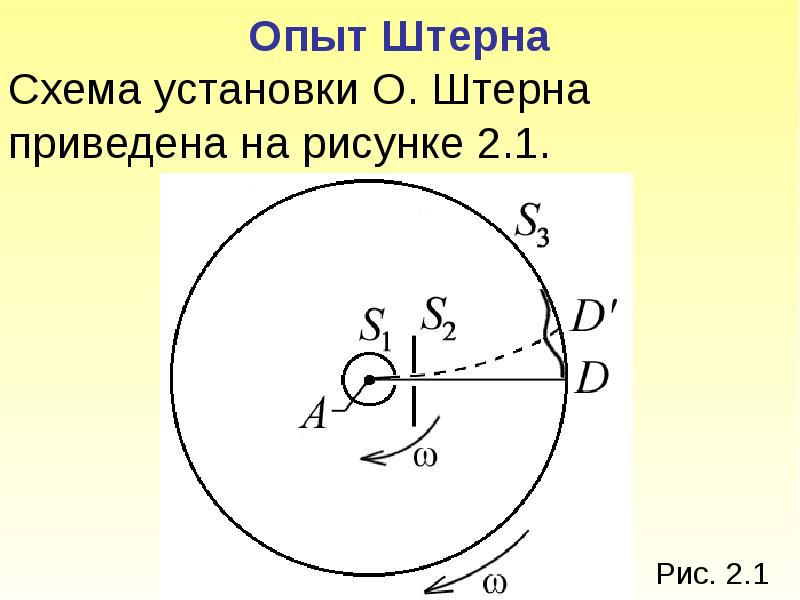
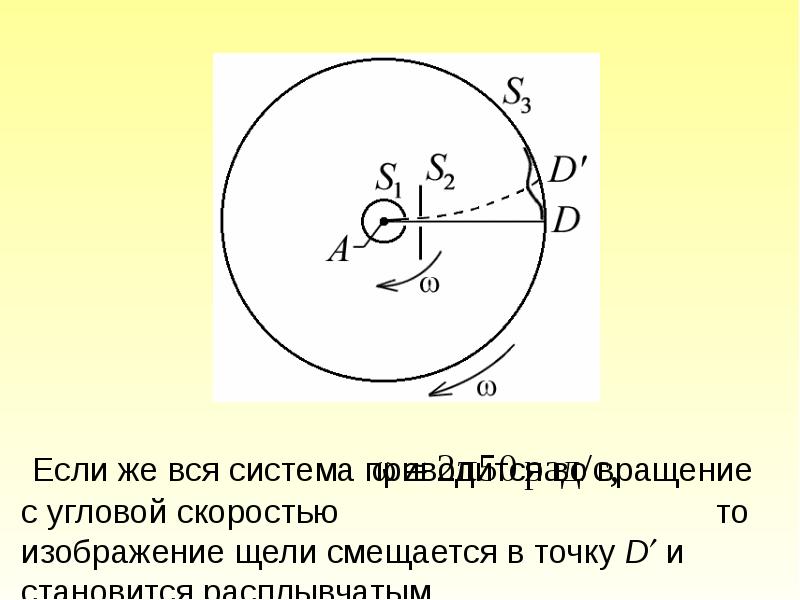
- 9. Опыт Штерна Схема установки О. Штерна приведена на рисунке 2.1.
- 10. Платиновая нить А, покрытая снаружи серебром, располагается вдоль оси коаксиальных цилиндров
- 11. Опыт Штерна Если же вся система
- 12. Пусть l – расстояние между D и, измеренное вдоль поверхности цилиндра
- 13. Температура нити в опытах Штерна равнялась 1200С, что соответствует среднеквадратичной скорости
- 14. Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно сталкиваясь
- 15. 2.2. Вероятность события. Понятие о распределении молекул газа по скоростям
- 16. Большое число сталкивающихся атомов и молекул обуславливает важные закономерности в поведении
- 17. Математическое определение вероятности: вероятность какого-либо события – это предел, к которому
- 19. Определить распределение молекул по скоростям вовсе не значит, что нужно определить
- 20. Итак, молекулы движутся хаотически. Среди них есть и очень быстрые, и
- 23. Мы будем искать число частиц (n) скорости которых лежат в определённом
- 24. Ясно так же, что n должно быть пропорционально концентрации молекул (n).
- 25. И так,
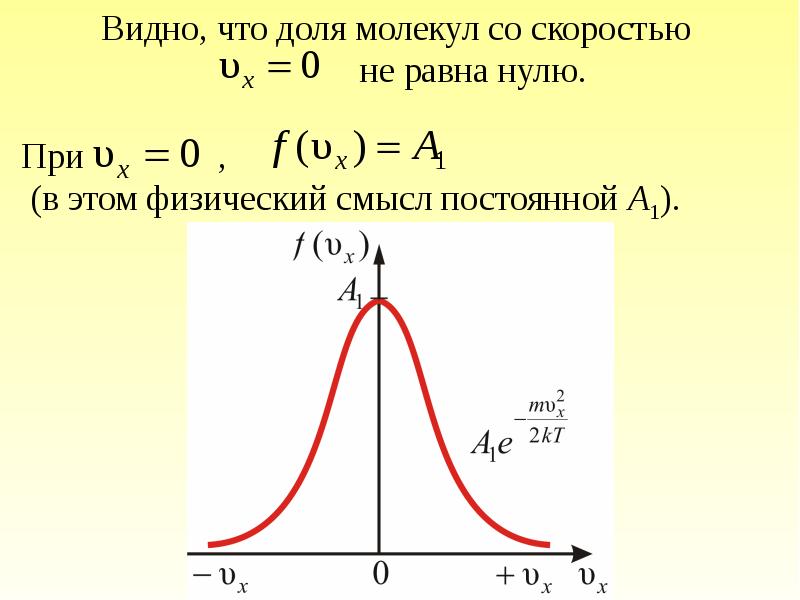
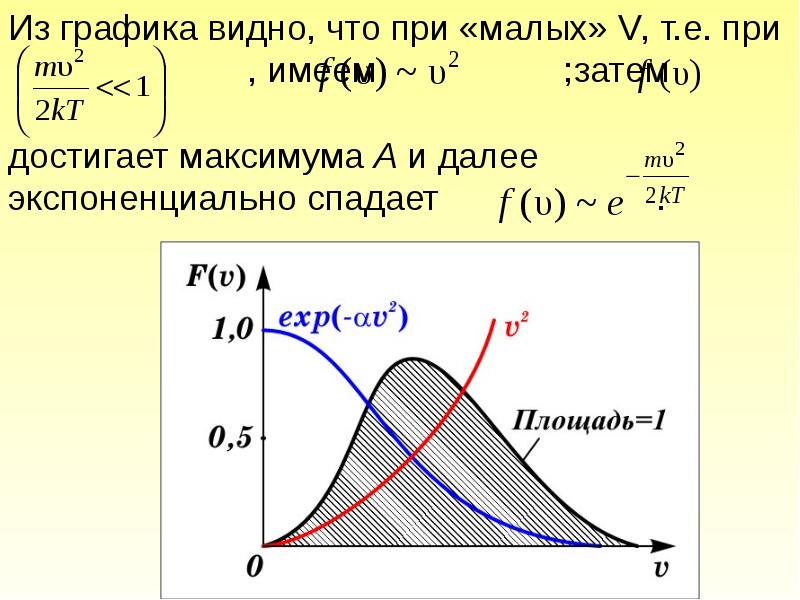
- 26. Таким образом, f(υ) – имеет смысл вероятности, то есть показывает, какова
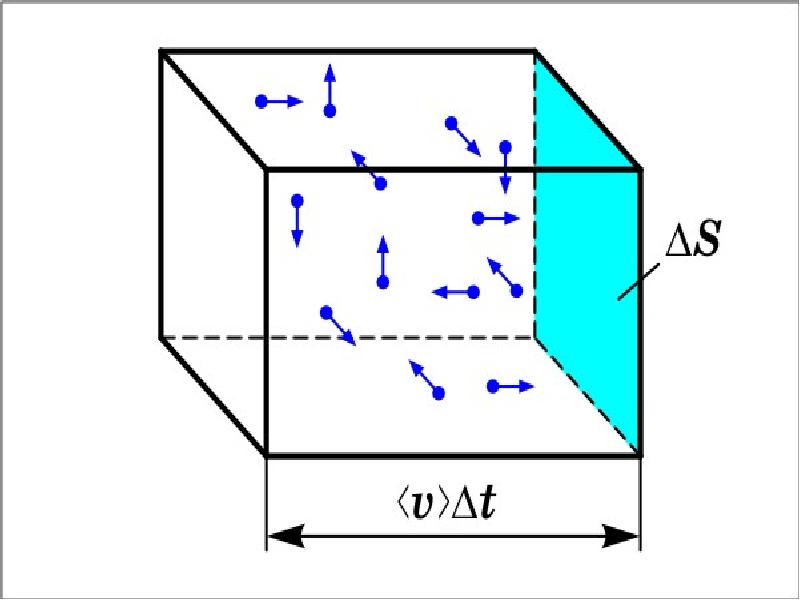
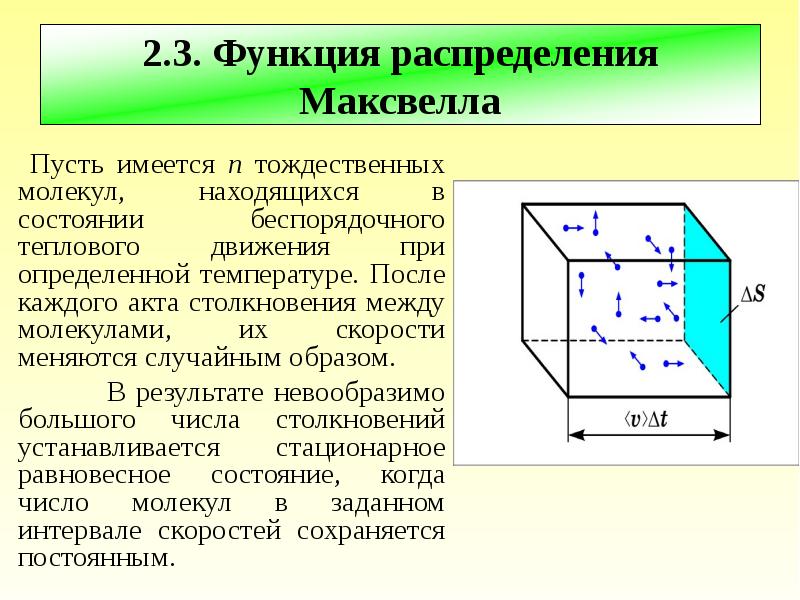
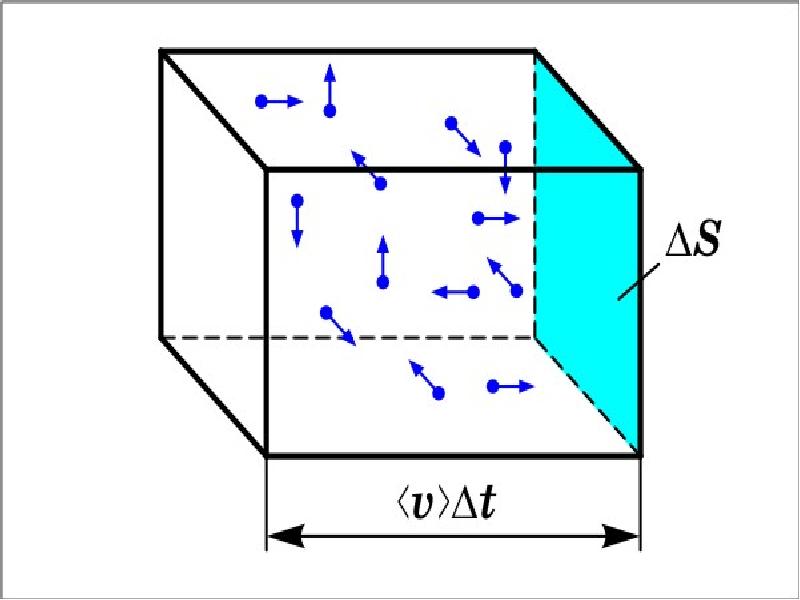
- 27. Пусть имеется n тождественных молекул, находящихся в состоянии беспорядочного теплового движения
- 28. В результате каждого столкновения проекции скорости молекулы испытывают случайное изменение на
- 29. При этом, мы не можем ничего определенного сказать о точном значении
- 30. Максвелл Джеймс Клерк (1831 – 1879)
- 31. Вывод формулы функции распределения молекул по скоростям есть в учебнике Ю.И
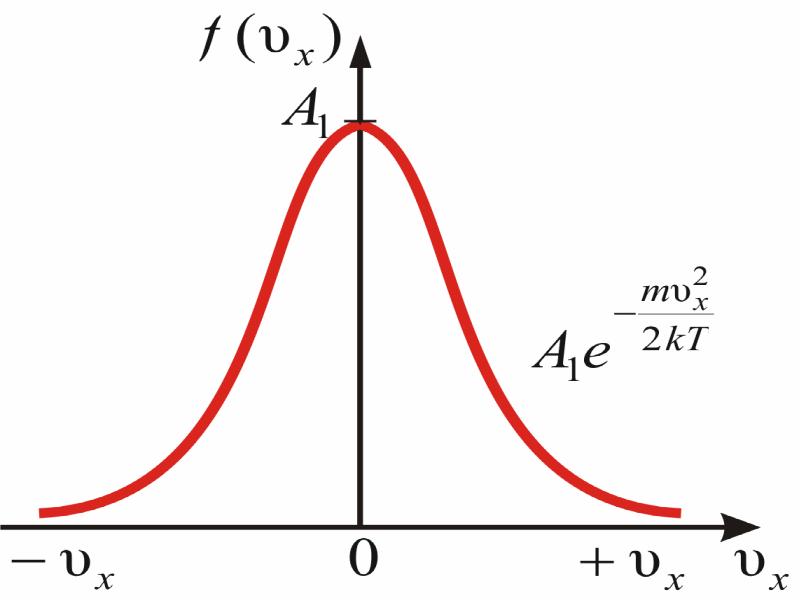
- 33. Скорость – векторная величина. Для проекции скорости на ось х (x-ой
- 36. Приведённое выражение и график справедливы для распределения молекул газа по x-ым
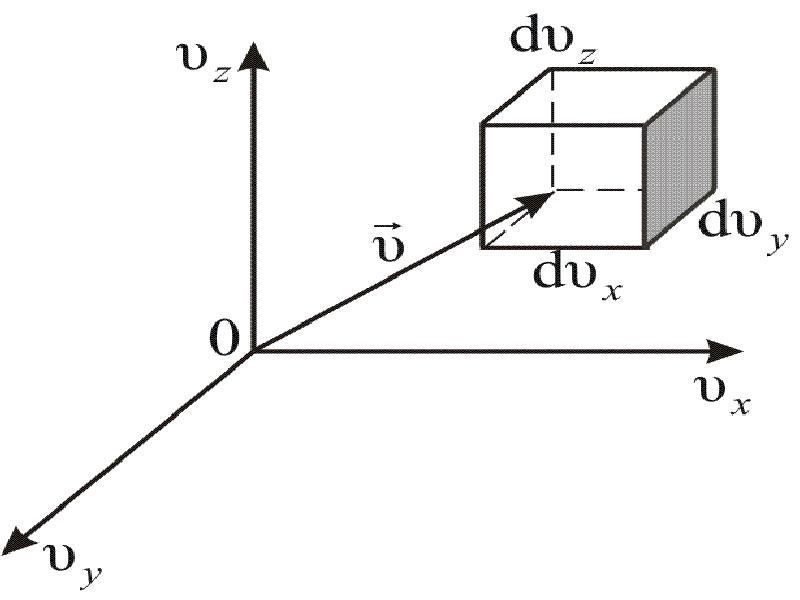
- 37. Вероятность того, что скорость молекулы одновременно удовлетворяет трём условиям: x –
- 38. Или
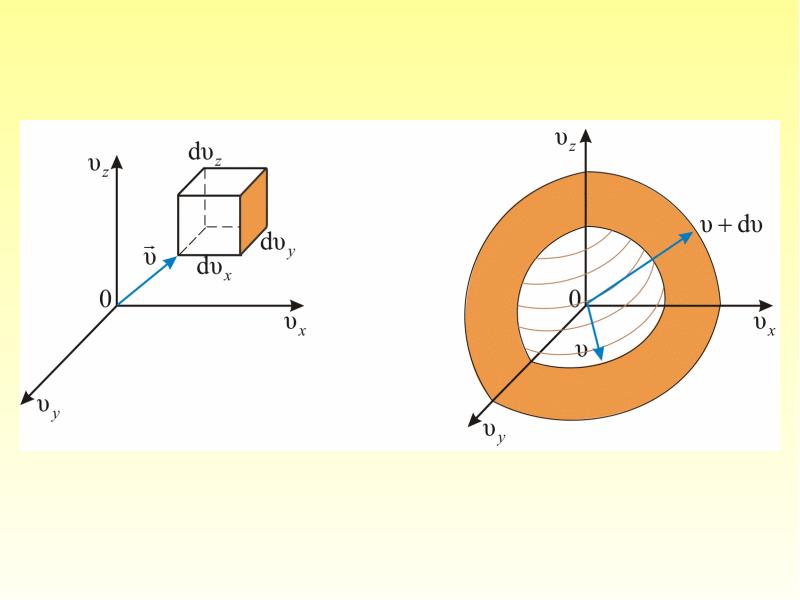
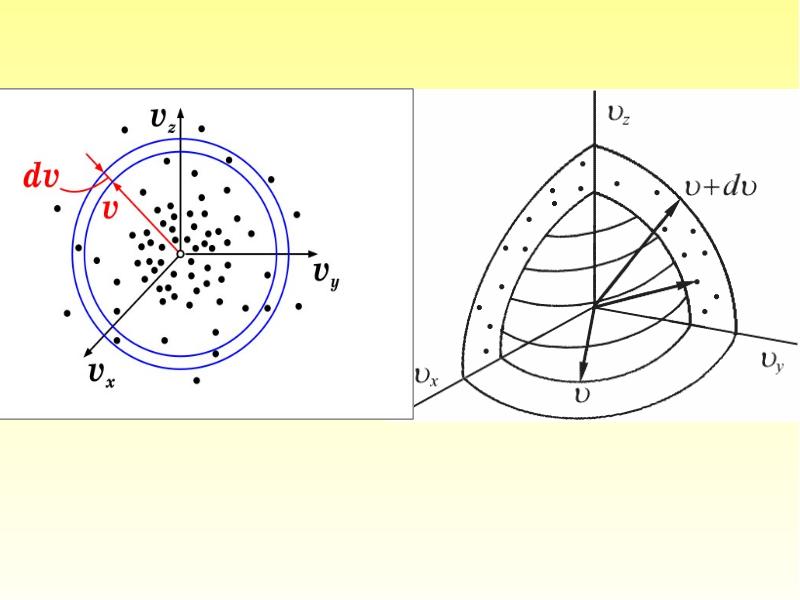
- 40. Величина (dnxyz) не может зависеть от направления вектора скорости. Поэтому надо
- 43. Этот шаровой слой складывается из тех параллелепипедов, о которых говорилось выше.
- 44. Отсюда следует закон Максвелла – распределение молекул по абсолютным значениям скоростей:
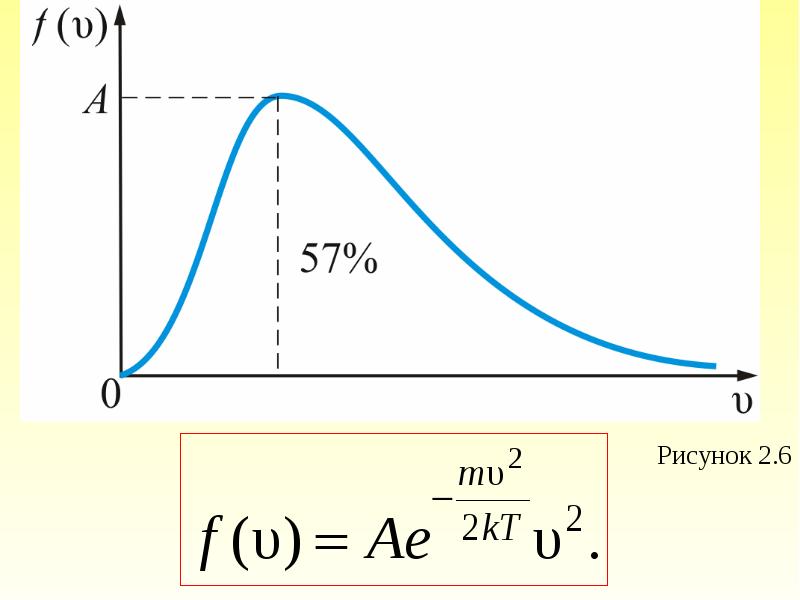
- 45. При получаем плотность вероятности, или функцию распределения молекул
- 46. Обозначим тогда,
- 48. Выводы: - Вид распределения молекул газа по скоростям, для каждого газа
- 49. Значит распределение Максвелла характеризует распределение молекул по значениям кинетической энергии (то
- 51. Рассмотрим пределы применимости классического описания распределения частиц по скоростям.
- 52. Здесь –
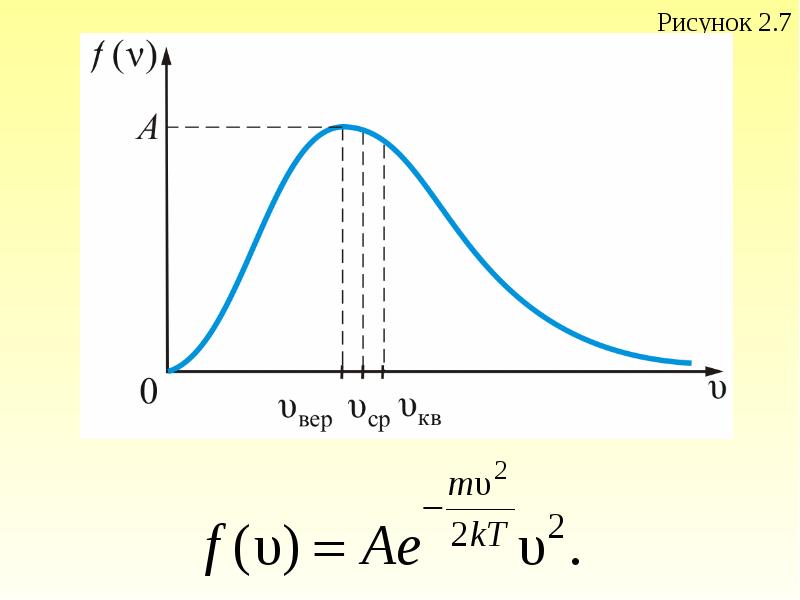
- 53. Наиболее вероятная, среднеквадратичная и средняя арифметическая скорости молекул газа Рассмотрим, как
- 56. Величина скорости, на которую приходится максимум зависимости называют наиболее
- 57. – наиболее вероятная скорость одной молекулы. для одного моля газа:
- 58. Среднюю квадратичную скорость найдем используя соотношение :
- 59. Средняя арифметическая скорость υср где
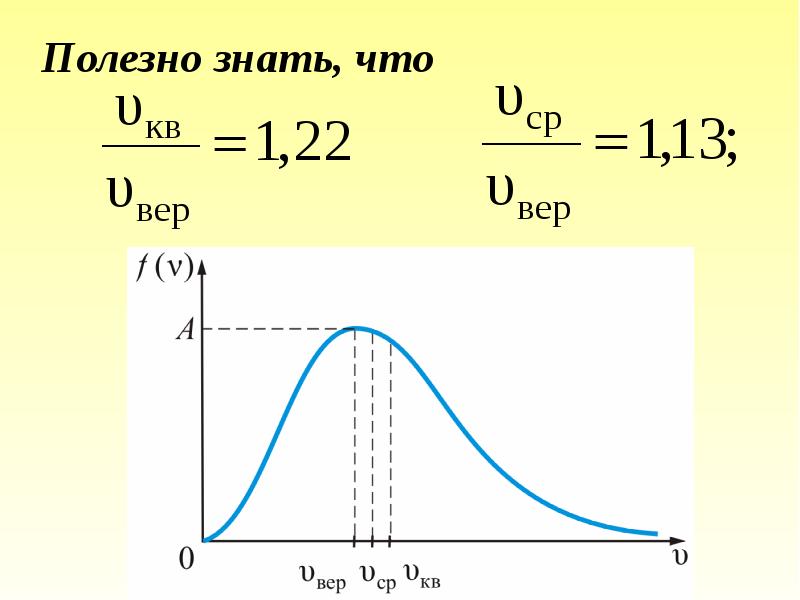
- 60. Полезно знать, что
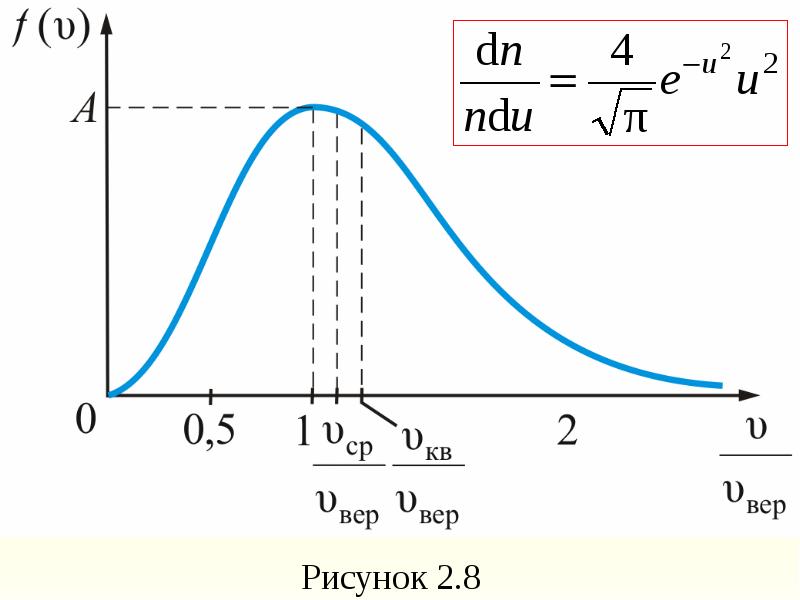
- 61. Формула Максвелла для относительных скоростей Для решения многих задач удобно
- 62. Это уравнение универсальное. В таком виде функция распределения не зависит ни
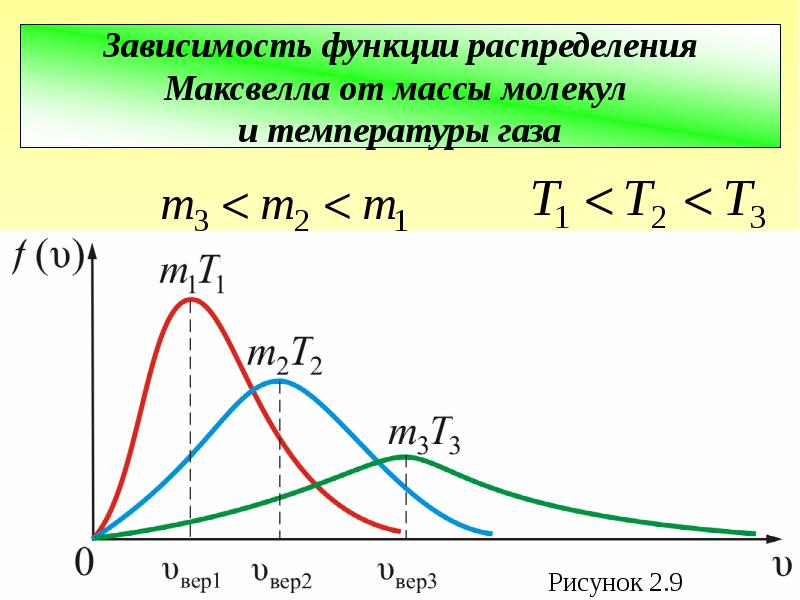
- 65. Из рис. 2.9 можно проследить за изменением при изменении
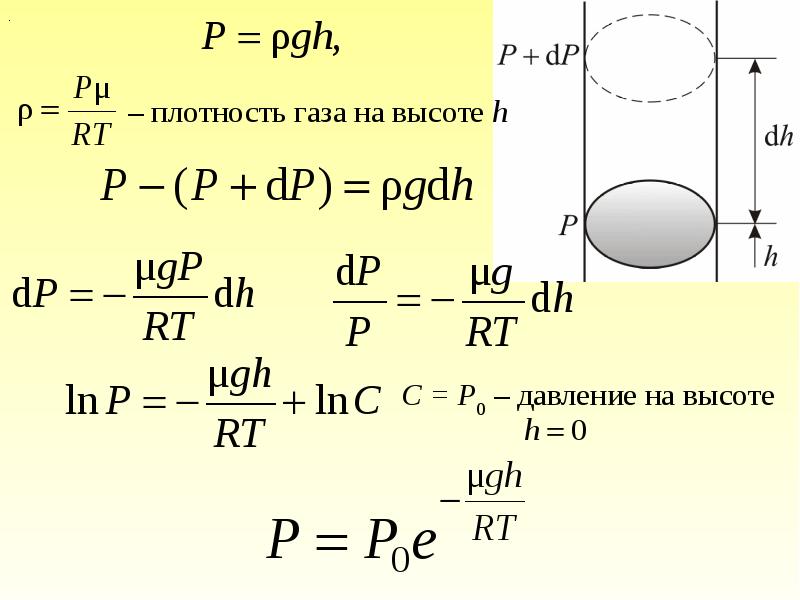
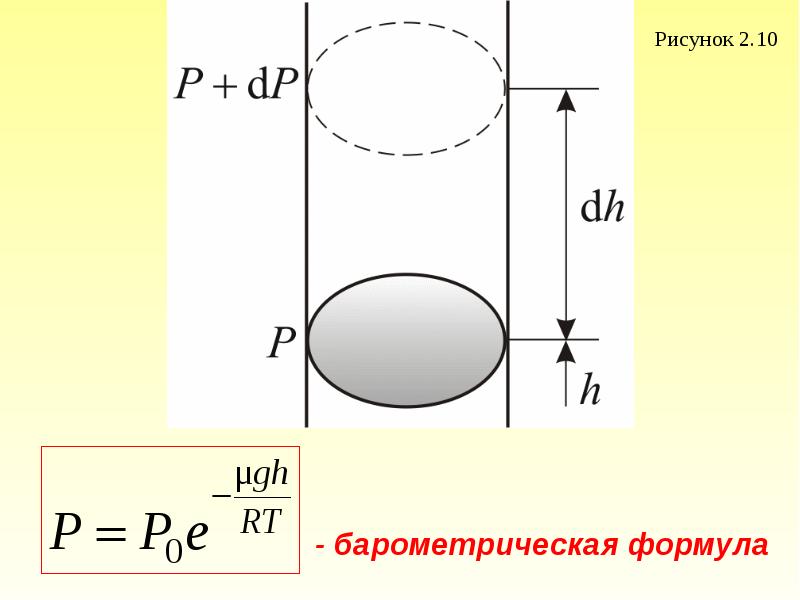
- 66. 2.4. Барометрическая формула Рассмотрим ещё один, очень важный закон.
- 69. Причём , dР < 0, так как на
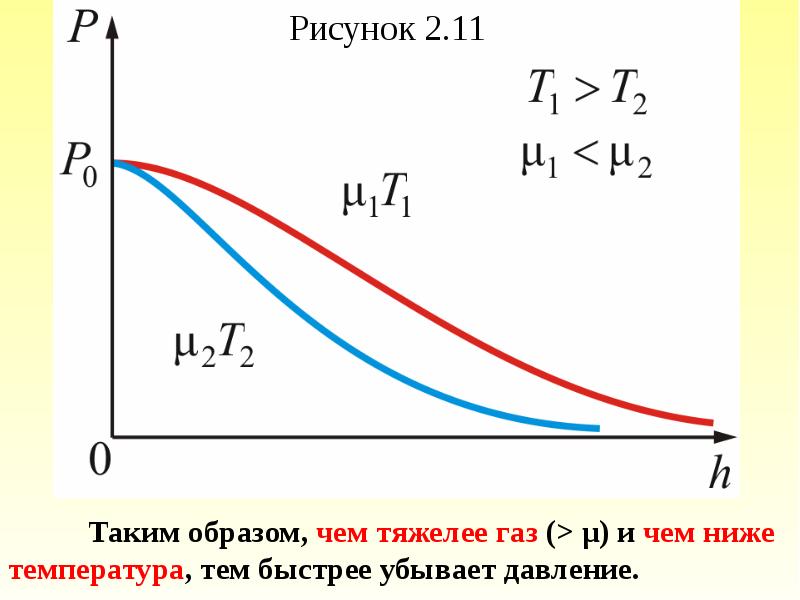
- 70. Из барометрической формулы следует, что P убывает с высотой тем быстрее,
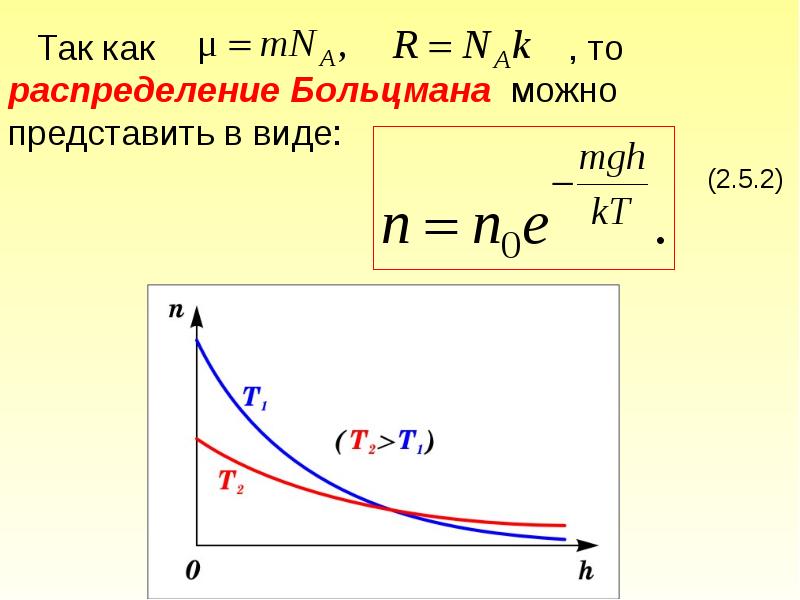
- 72. Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового
- 73. Больцман Людвиг (1844 – 1906) –
- 74. Пусть идеальный газ находится в поле консервативных сил, в условиях теплового
- 75. Если известно число молекул в единичном объеме, то известно и давление,
- 76. Исходя из основного уравнения молекулярно-кинетической теории: , заменим
- 79. С уменьшением температуры число молекул на высотах, отличных от нуля, убывает.
- 80. Так как –потенциальная энергия, следовательно, распределение Больцмана
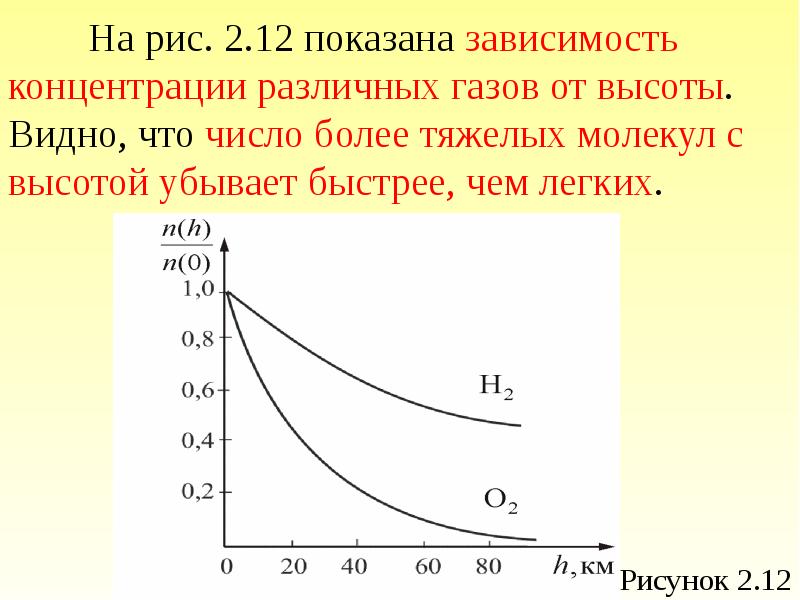
- 81. На рис. 2.12 показана зависимость концентрации различных газов от высоты. Видно,
- 82. Из (2.5.3) можно получить, что отношение концентраций молекул в точках с
- 83. 2.6. Закон распределения Максвелла-Больцмана В п. 2.3 мы получили выражение
- 84. Из этого выражения легко найти распределение молекул газа по значениям кинетической
- 85. Отсюда получим функцию распределения молекул по энергиям теплового движения:
- 86. Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии а
- 87. Обозначим – полная энергия. Тогда
- 88. В последнем выражении, потенциальная и кинетическая энергии, а следовательно и полная
- 89. где Ni – число частиц, находящихся в состоянии с энергией Еi,
- 90. Тогда, окончательное выражение распределения Масвелла-Больцмана для случая дискретных значений будет иметь
- 91. 2.7. Распределение Бозе-Эйнштейна, Ферми-Дирака Если у нас имеется термодинамическая
- 92. Основная задача этой статистики состоит в определении среднего числа
- 93. распределение Бозе-Эйнштейна:
- 94. Первая формула описывает квантовые частицы с целым спином (собственный момент количетсва
- 96. Скачать презентацию








































































Слайды и текст этой презентации
Скачать презентацию на тему Распределение газовых молекул по скоростям и энергиям (Тема 2) можно ниже:
Похожие презентации