Распределение Максвелла. Распределение Больцмана презентация

Лекция 17 Распределение Максвелла Распределение Больцмана

Распределение Максвелла В лекции 16 было введено понятие о вероятностях для молекул dW(vх), dW(vу) и dW(vz) иметь проекцию скорости движения в интервалах Обобщением будет введение понятия вероятности dW( ) иметь определенное значение вектора скорости

Распределение Максвелла В геометрическом смысле это означает вероятность того, что в пространстве скоростей конец вектора скорости находится в параллелепипеде объемом Как и для любой непрерывной случайной величины, для dW( ) должно выполняться условие  

Распределение Максвелла Закон распределения молекул по скоростям был получен в конце 19 века Максвеллом. При этом он сделал два предположения: 1. все направления скоростей равновероятны 2. рассчитанное с помощью закона распределения давление идеального газа должно соответствовать полученному из экспериментов уравнению.

Распределение Максвелла Для непрерывной случайной величины, каковой является скорость молекулы, можно ввести функцию распределения (плотность вероятности) , такую, что   .   Из принципа равновероятности направлений движения следует, что плотность вероятности не зависит от угловых переменных, указывающих направление вектора скорости, а должна быть лишь функцией его модуля:   .

Распределение Максвелла Аналогично можно ввести функции распределения f(vх), f(vy) и f(vz) определяющие вероятности, что молекула имеет компоненты скорости в малых интервалах   , , .

Распределение Максвелла В силу хаотичности молекулярного движения, каждая из функций распределения зависит только от "своей" компоненты скорости и не зависит от других. Вид этих функций один и тот же независимо от выбора аргумента vx, vy или vz. Это позволяет для функциональной зависимости от проекций скоростей используется одно и то же обозначение f. Отметим, что  

Распределение Максвелла Обладание тем или иным значением одной компоненты скорости никак не зависит от величины других компонент. В соответствии с принципом умножения вероятностей для независимых событий имеем соотношение     Здесь под событием подразумевается обнаружение определенного значения одной из компонент скорости.

Распределение Максвелла Для плотностей вероятностей f(vх), f(vy) и f(vz) получаем    Прологарифмируем это выражение     и продифференцируем по   .

Распределение Максвелла Поскольку , для производной получим следующее значение   .   Теперь уравнение может быть представлено в виде   .

Распределение Максвелла Из равенства (17.8) следует, что функции различных аргументов совпадают друг с другом во всей области их определения. Такое может быть, только если они все равны одной и той же постоянной. Поэтому перепишем (17.8) и аналогичные выражения для проекций в виде  .   где α – некоторая константа. Множитель –2 перед ней выбран из соображений, которые станут понятны ниже.

Распределение Максвелла Проведем интегрирование) четырех уравнений вида     Вначале разделим переменные   .  После интегрирования получаем     где Z –константа.

Распределение Максвелла Окончательно получаем   .   Тем же путем получим выражения для функций распределения компонент скорости   , , .

Распределение Максвелла Постоянная Z0 может быть найдена из условия     Интеграл вида называется интегралом Пуассона. В математическом анализе показано, что его значение равно   .

Распределение Максвелла Отсюда получаем для   Между Z и Z0 существует простая связь  

Распределение Максвелла Окончательно получаем для функций распределения следующие выражения , , . .

Распределение Максвелла Перейдем теперь к определению константы α. В лекции 16 мы показали, что давление идеального газа на стенку сосуда равно   .   Чтобы найти α, нужно вычислить и подставить в это выражение

Распределение Максвелла В соответствии с теорией вероятностей   .   В итоге получаем   .

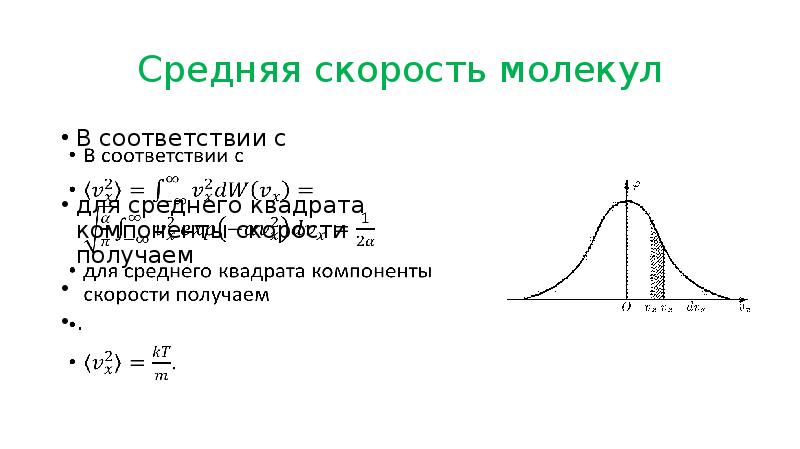
Средняя скорость молекул Вероятность молекул газа иметь компонент скорости (например, ) в интервале     График зависимости функции распределения от

Средняя скорость молекул Среднее значение компоненты скорости можно вычислить по формуле   Максимум функции распределения по компоненте скорости приходится на 0. Наиболее вероятной является нулевая компонента скорости молекулы.

Средняя скорость молекул В соответствии с для среднего квадрата компоненты скорости получаем   .

Средняя скорость молекул Отсюда легко получить выражение для средней энергии движения по выделенному направлению     И полную среднюю кинетическую энергию молекул   .  

Средняя скорость молекул Вероятность найти в газе молекулу со скоростью равна   .  

Средняя скорость молекул Нашей дальнейшей задачей является нахождения среднего модуля скорости молекул Для этого необходимо перейти к распределению по скоростям в сферических координатах. В свою очередь, для этого нужно записать выражение для элемента объема в сферических координатах  

Средняя скорость молекул Распределение по скоростям в сферических координатах   . (17.24)   Это не что иное, как вероятность двигаться со скоростью по направлению, задаваемому углами  и . В задаче о нахождении средней скорости молекул направление не важно, поэтому мы можем проинтегрировать это выражение по углам  

Средняя скорость молекул .   В итоге мы получаем вероятность найти в газе молекулу с модулем скорости, лежащим в интервале .   .

Средняя скорость молекул В геометрическом смысле это выражение определяет вероятность того, что в пространстве скоростей конец вектора скорости попадает в сферический слой между объемом 4

Средняя скорость молекул Теперь мы можем найти средний модуль скорости (среднюю скорость) молекул  . А также средний квадрат модуля скорости   Величину называют среднеквадратичной скоростью молекул

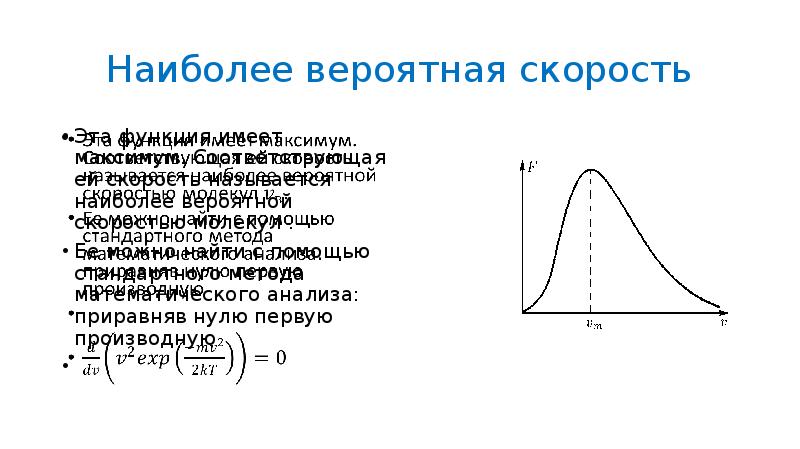
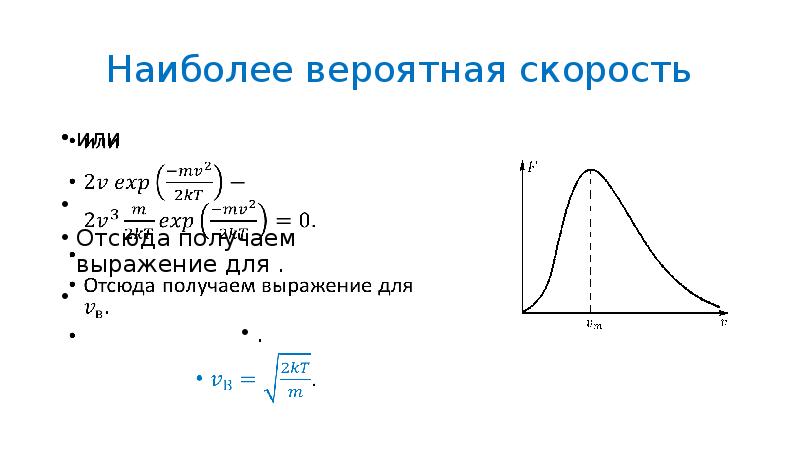
Наиболее вероятная скорость Эта функция имеет максимум. Соответствующая ей скорость называется наиболее вероятной скоростью молекул . Ее можно найти с помощью стандартного метода математического анализа: приравняв нулю первую производную  

Наиболее вероятная скорость или    Отсюда получаем выражение для .   .

Наиболее вероятная скорость Введя относительную скорость , как отношение скорости молекулы к наиболее вероятной получим распределение по абсолютной величине скорости в виде   Отсюда доля молекул, скорость которых больше u будет определяться интегралом В таблице 1 приведены некоторые значения этого интеграла.  

Наиболее вероятная скорость

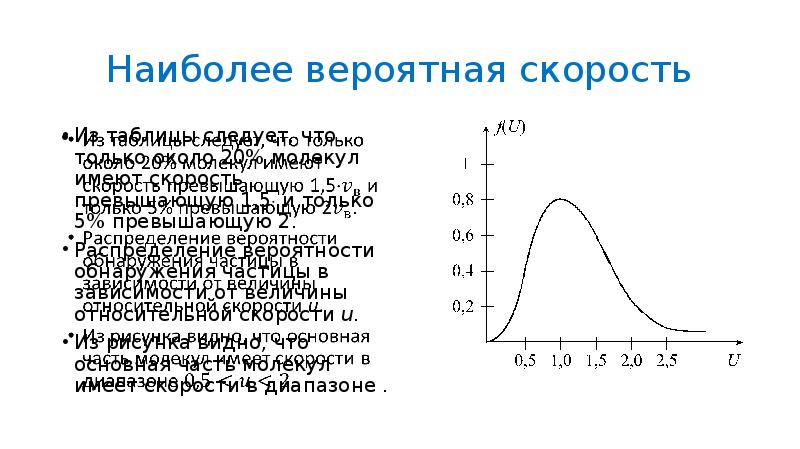
Наиболее вероятная скорость Из таблицы следует, что только около 20% молекул имеют скорость превышающую 1,5 и только 5% превышающую 2. Распределение вероятности обнаружения частицы в зависимости от величины относительной скорости u. Из рисунка видно, что основная часть молекул имеет скорости в диапазоне .

Молекулярные пучки (потоки) Надем поток молекул в вакуум через малое отверстие в стенке сосуда. Если размер отверстия много меньше длины свободного пробега молекул, то столкновений в отверстии не будет, а концентрация молекул будет возмущена в области порядка размера отверстия.

Молекулярные пучки (потоки) Если отверстие находится в стенке лежащей в плоскости Z,Y то попадание на стенку и соответственно в отверстие будет определяться молекулами имеющими не нулевую компоненту скорости

Молекулярные пучки (потоки) Количество молекул dj, имеющих компоненту скорости от и пролетающих через отверстие в единицу времени равно   ,   где n – концентрация молекул, S – площадь отверстия.

Молекулярные пучки (потоки) Полный поток через отверстие J можно получить, интегрируя по компоненте скорости. Поскольку нас интересуют только молекулы летящие к отверстию, а не в противоположную сторону, интеграл берется от .   .

Молекулярные пучки (потоки) Распределение молекул в потоке по скоростям отличается от распределения в по скоростям в замкнутом объеме. Дело в том, что в объеме молекулы постоянно сталкиваются друг с другом, а в потоке вероятность их столкновения крайне мала. Поэтому отличаются от «объемных» средние величины скоростей и средняя энергия молекул в потоке <Ej>.

Молекулярные пучки (потоки) , , .

Молекулярные пучки (потоки) Значения средних величин в потоке больше, чем у соответствующих им величин в объеме. Например, средняя энергия в потоке на больше, чем средняя энергия в объеме. Это связано с тем, что более быстрые молекулы чаще сталкиваются со стенкой и соответственно чаще вылетают из отверстия. Поэтому их вклад в среднюю энергию больше, чем у медленных молекул

Закон равнораспределения энергии по степеням свободы Как мы уже отмечали, средняя энергия поступательного движения. Учитывая независимость распределения по скоростям движения по различным осям мы приходим к выводу, что на каждую поступательную степень свободы приходится энергия . Заметим, что средняя энергия не зависит от массы молекулы. Это означает, что в смеси газов молекулы с различной массой будут иметь разные скорости, но одинаковую кинетическую энергию.

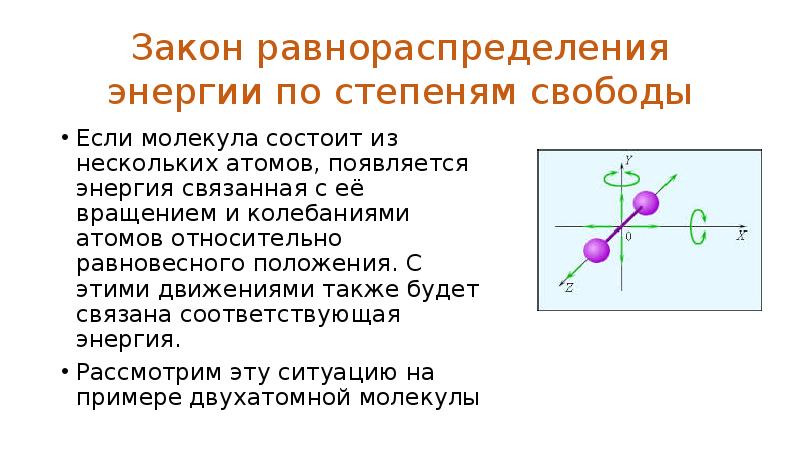
Закон равнораспределения энергии по степеням свободы Если молекула состоит из нескольких атомов, появляется энергия связанная с её вращением и колебаниями атомов относительно равновесного положения. С этими движениями также будет связана соответствующая энергия. Рассмотрим эту ситуацию на примере двухатомной молекулы

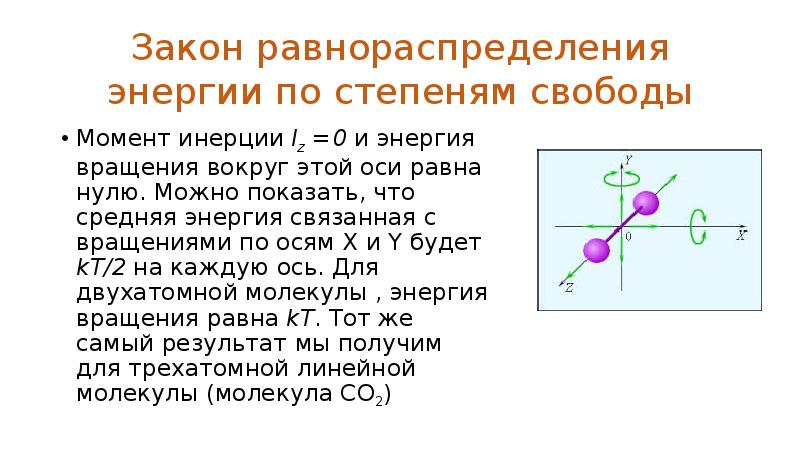
Закон равнораспределения энергии по степеням свободы Момент инерции Iz =0 и энергия вращения вокруг этой оси равна нулю. Можно показать, что средняя энергия связанная с вращениями по осям X и Y будет kT/2 на каждую ось. Для двухатомной молекулы , энергия вращения равна kT. Тот же самый результат мы получим для трехатомной линейной молекулы (молекула СО2)

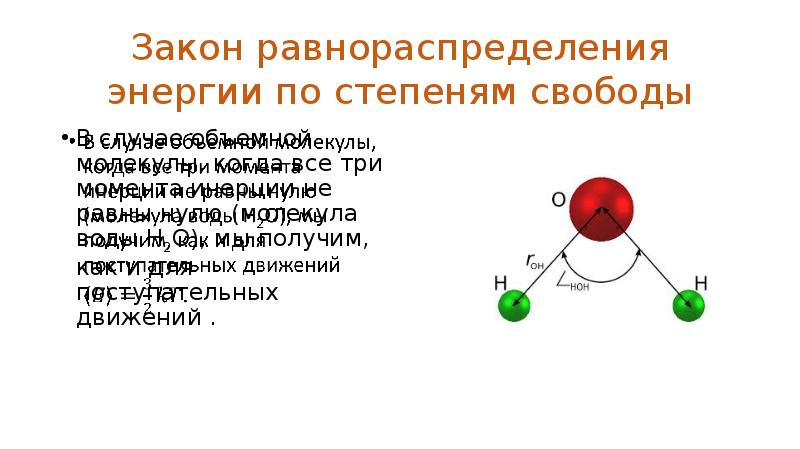
Закон равнораспределения энергии по степеням свободы В случае объемной молекулы, когда все три момента инерции не равны нулю (молекула воды Н2О), мы получим, как и для поступательных движений .

Закон равнораспределения энергии по степеням свободы При колебаниях атомов в молекуле энергия будет состоять из потенциальной энергии связанной с смещением молекул относительно положения равновесия и кинетической энергией их движения в этот момент. Учитывая это в мы получим, что на каждую колебательную степень свободы приходится энергия .

Закон равнораспределения энергии по степеням свободы Квантовая природа молекулярных движений вносит коррективы в эту простую картину. Энергия может изменяться дискретными порциями – квантами. Поэтому когда температура мала – меньше первого уровня изменения энергии, соответствующая степень свободы не возбуждена и не вносит вклад в энергию хаотического движения. Поступательные степени свободы появляются при очень низких температурах, затем при повышении температуры начинают возбуждаться вращательные степени свободы. При дальнейшем повышении температуры, когда , возбуждаются колебательные степени свободы. Соответственно теплоемкость газов будет увеличиваться с увеличением температуры, достигая максимума, когда возбуждены все степени свободы.

Барометрическая формула На практике часто приходится иметь дело с газом, находящимся в потенциальном внешнем поле. Важным примером такого поля является поле тяжести. Пусть ось z системы координат направлена вертикально вверх. Молекула газа в этом поле обладает потенциальной энергией, равной  .

Барометрическая формула Будем рассматривать газ в сосуде высотой h, с температурой, одинаковой во всех точках. Выберем в сосуде некоторый горизонтальный слой малой толщины dz Вес Р этого слоя компенсируется разностью давлений, действующих снизу и сверху: .

Барометрическая формула С другой стороны, вес газа равен просто весу всех его молекул. Введем плотность газа n(z), которая может зависеть от z. Если слой тонкий, можно пренебречь изменением n(z) в его пределах. Тогда вес определяется формулой:   .

Барометрическая формула Приравнивая получим     Если газ идеальный, то р = nkT, и   .

Барометрическая формула Интегрируя, получаем зависимость плотности от высоты:   . Полное число молекул N при этом есть       Отсюда определяется n(0):   .

Барометрическая формула Для условий земной атмосферы h0  10 км. Сооружаемые емкости имеют значительно меньшие габариты, поэтому неоднородность распределения паров в них не наблюдается. Лишь при подъеме в горы или с помощью авиации обнаруживается влияние поля тяжести на распределение воздуха в атмосфере.

Барометрическая формула Необходимо подчеркнуть, что формула применима только к изотермической "тонкой" атмосфере. Из нее следует барометрическая формула   .

Барометрическая формула Воздух представляет собой смесь газов, молекулы которых имеют различную массу. Состав атмосферы должен резко изменяться с высотой. Относительная концентрация легких газов должна увеличиваться с высотой. Измерения состава воздуха на разных высотах не подтвердили этого вывода. Интенсивная конвекция в пределах тропосферы приводит к известному выравниванию состава воздуха по высоте. Общеизвестно также падение температуры с высотой.

Распределение Больцмана Распределению молекул по высоте можно придать несколько иной вид. Вероятность обнаружить молекулу в слое толщиной dz на высоте z определяется долей dW(z) таких молекул от общего числа:     где U(z) – потенциальная энергия молекулы во внешнем поле; Z = N / n(0) – нормировочный множитель

Распределение Больцмана В произвольной системе координат распределение (17.42) будет иметь вид   где – элемент объема пространства. в декартовой системе координат ,  в сферической  ,  в цилиндрической  .

Распределение Больцмана Это распределение может использоваться для произвольного типа взаимодействия (то есть не обязательно гравитационного) и для любого вида пространственной зависимости потенциальной энергии (то есть не обязательно приводящей к однородному внешнему полю). Единственным ограничением является консервативный характер действующих сил – то есть это такие силы, для которых их работа при движению по замкнутому контуру равняется нулю. Только для таких сил можно ввести потенциальную энергию, которая зависит только от положения в пространстве.

Распределение Больцмана Это распределение называется распределением Больцмана. Нормировочная постоянная в Z находится из условия, что полная вероятность обнаружить молекулу равна единице и, следовательно   .

Центрифугирование, разделение изотопов Центрифугирование нашло широкое применение в химии и биологии как эффективный способ разделения близких по молекулярному весу или плотности веществ. В системе отсчета, связанной с центрифугой, объект исследования находится в равновесии, и к нему можно применить распределение Больцмана.

Центрифугирование, разделение изотопов на частицы действует центробежная сила. Соответствующая потенциальная энергия частицы равна   .   Распределение Больцмана с учетом цилиндрической симметрии имеет вид   ,   где – длина барабана центрифуги.

Центрифугирование, разделение изотопов Для концентрации частиц получается формула   .

Центрифугирование, разделение изотопов Из формулы следует, что концентрация тяжелых частиц у боковой стенки центрифуги относительно выше, что используется для разделения смесей. Сейчас особенно активно центрифугирование используется для разделения составляющих различных биологических препаратов. Также центрифугирование было использовано для обогащения урана. Уран состоит в основном из двух изотопов 238U (99,28 % природного содержания) и 235U (0,71 %). Cпособностью к ядерным реакциям деления обладает только изотоп 235U. Возникающая задача обогащения урана решалась путем его фторирования, с образованием газообразного соединения UF6, и последующего многократного центрифугирования

До следующей лекции