Решение алгебраических и трансцендентных уравнений презентация

Решение алгебраических и трансцендентных уравнений

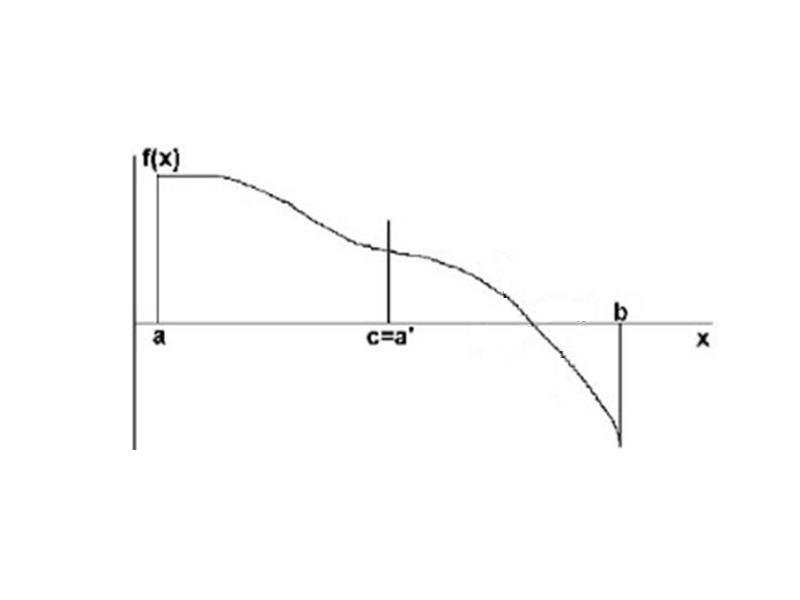
Алгоритм данного метода: Алгоритм данного метода: 1.Определить начальные данные (a, b, ). 2.Если нужная точность достигнута (| b - a | < ) то п.6 3.Найти середину очередного отрезка (c=(a+b)/2). 4.Если значения функции в точках а и c одного знака (f(a)*f(c)>0), то в качестве следующего отрезка взять правую половину (а=c), иначе левую (b=c). 5.Иди к п.2. 6.Напечатать ответ (( a + b ) / 2 )

Методом половинного деления уточнить корень уравнения Методом половинного деления уточнить корень уравнения x4 + 2 x3 – x – 1 = 0 лежащий на отрезке 0, 1.

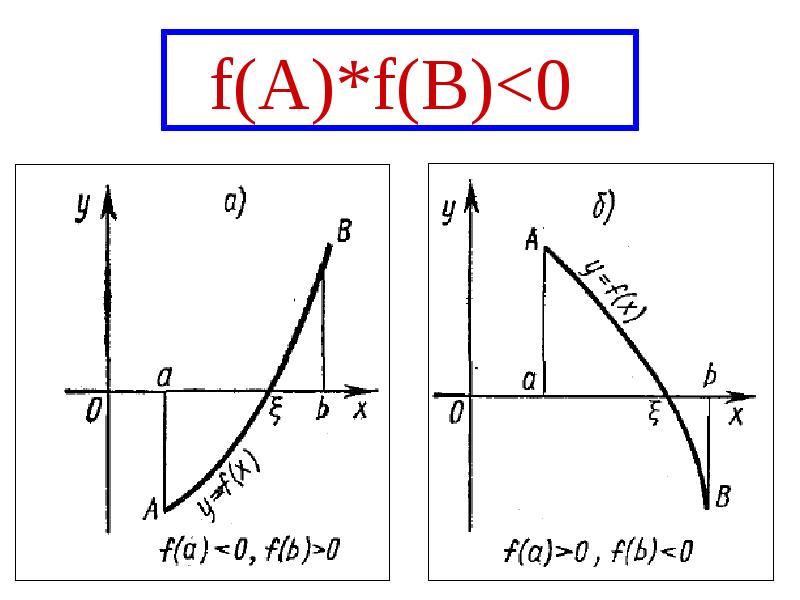
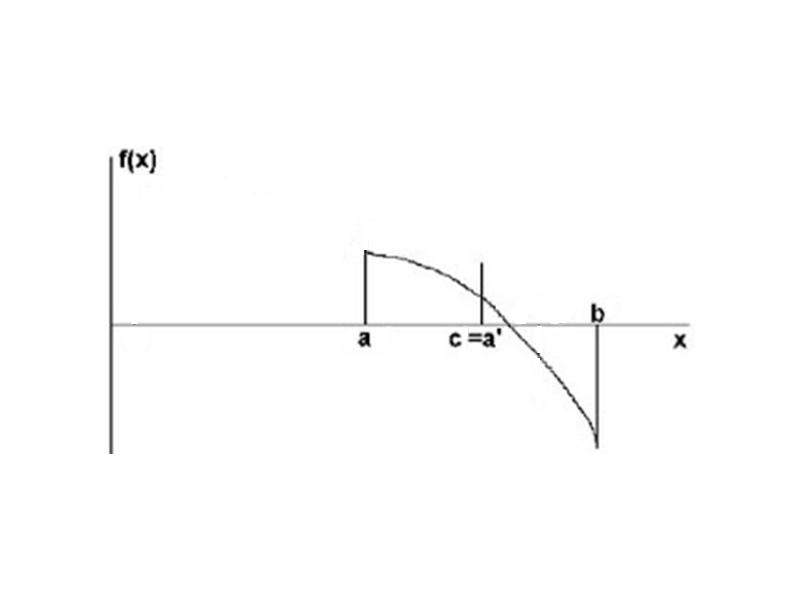
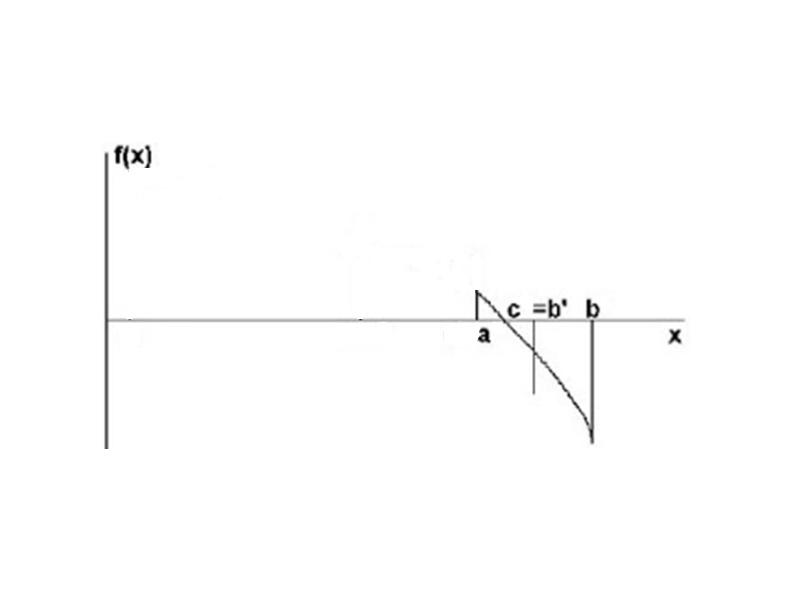
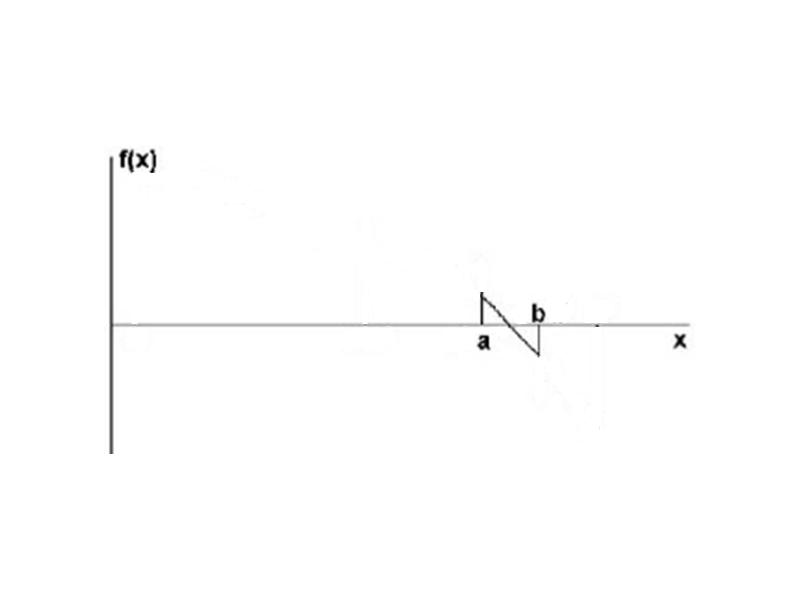
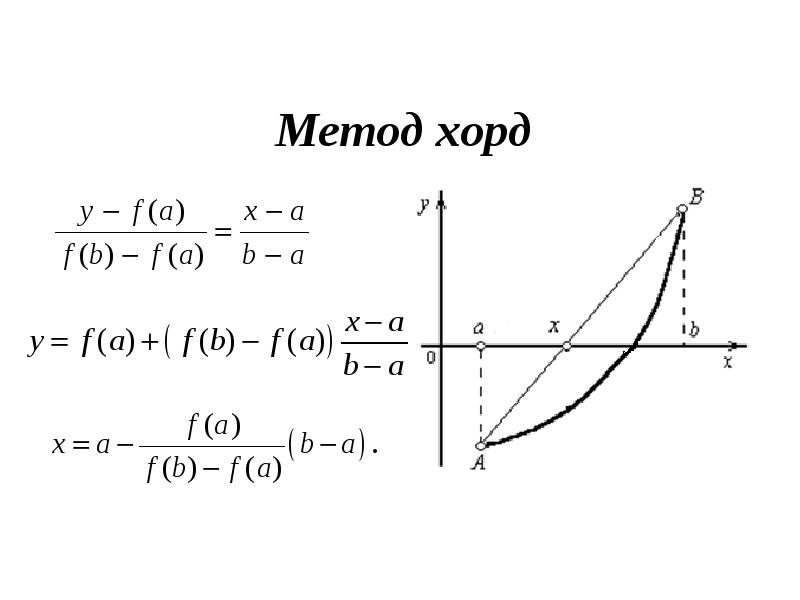
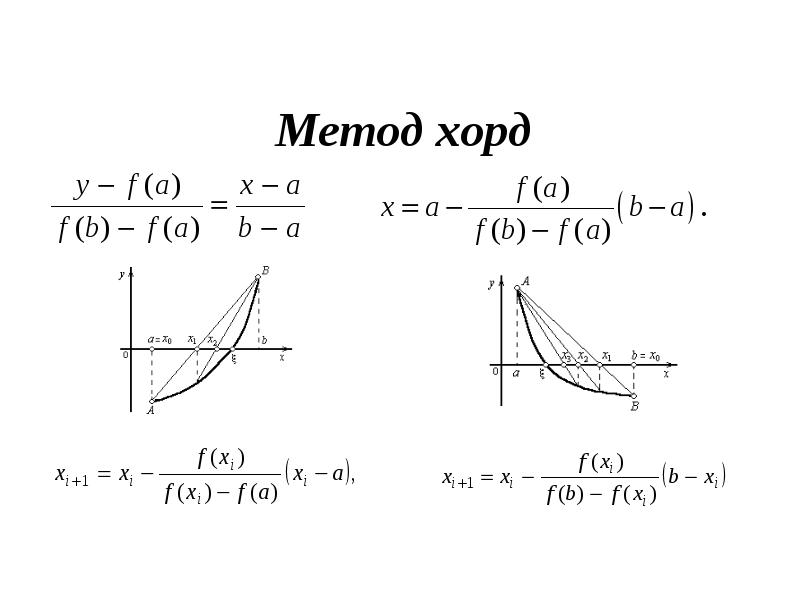
Метод хорд Применяется в том случае, когда f'(X) и f''(X) не изменяют знака на отрезке [a,b], т.е. функция f(X) на отрезке [a,b] монотонна и не имеет точек перегиба

Метод хорд

Метод хорд

Найти положительный корень уравнения (методом хорд) x3 – 0,2 x2 – 0,2 х – 1,2 = 0 с точностью  = 0,01.

Метод Ньютона (касательной) В качестве исходной точки х0 выбирается тот конец интервала [а, b], которому отвечает ордината того же знака, что и знак f  (х).

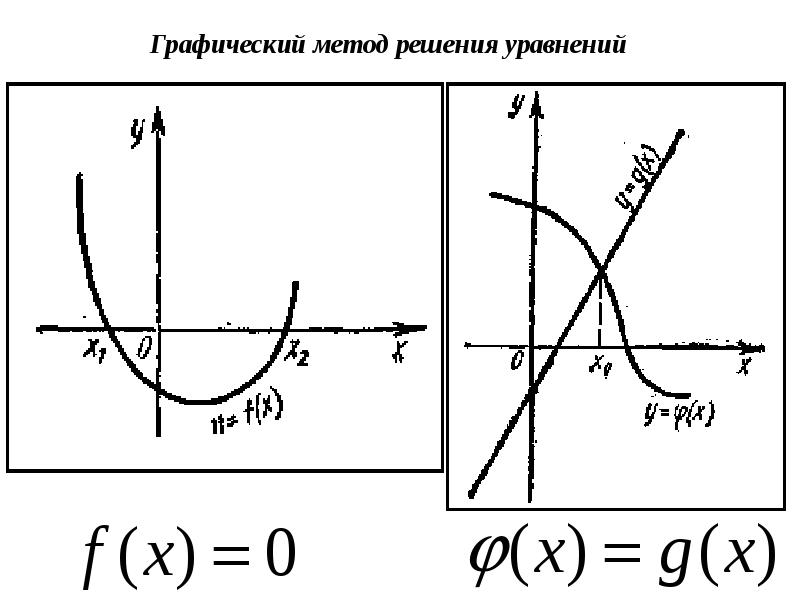
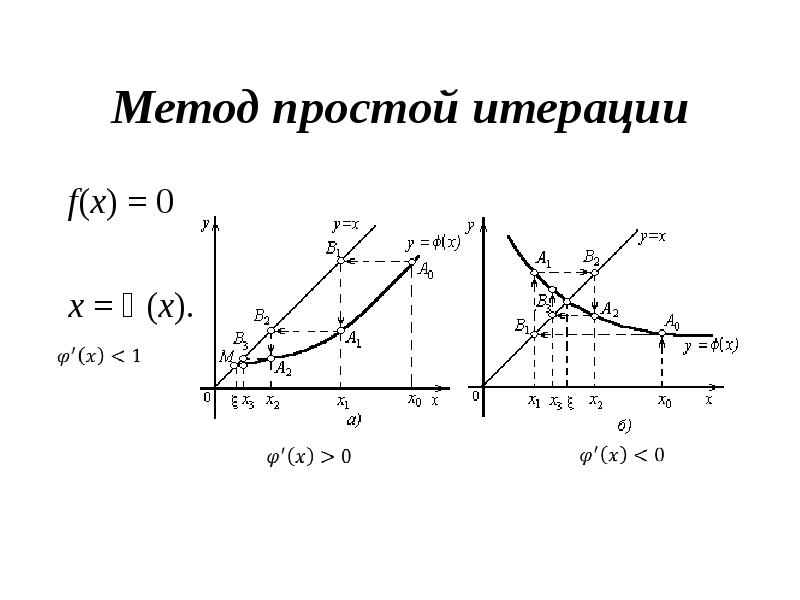
Метод простой итерации f(х) = 0 x = ϕ(x).

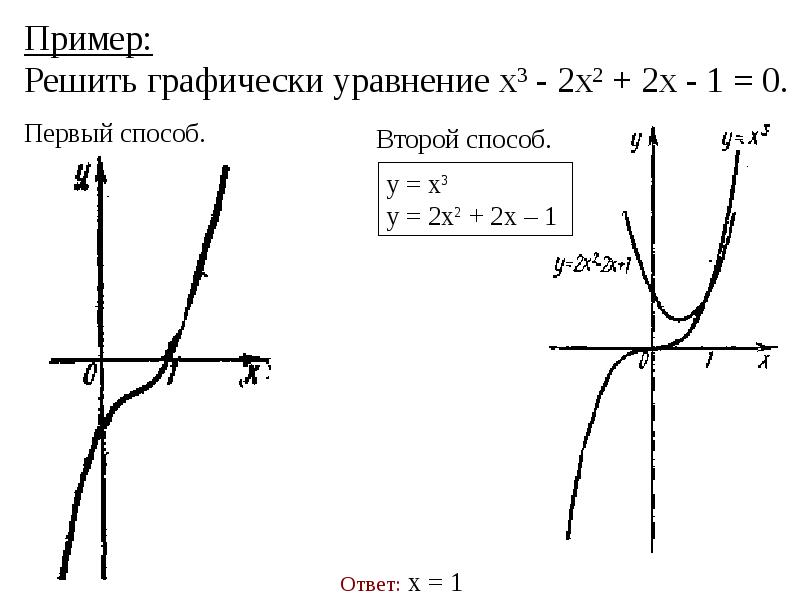
Решить уравнение x3 – x – 1 = 0, на интервале 1<x<2