Решение тригонометрических уравнений и способы отбора корней на заданном промежутке презентация
Содержание
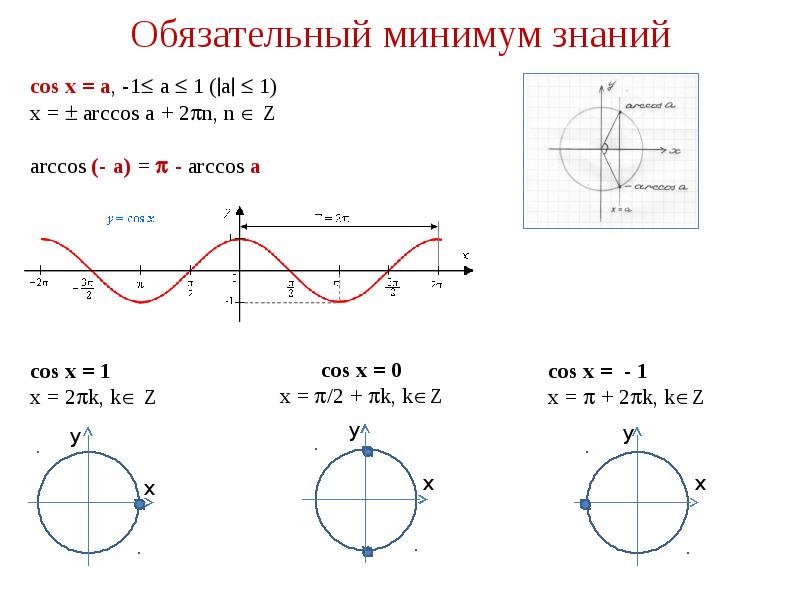
- 2. Обязательный минимум знаний
- 3. Обязательный минимум знаний
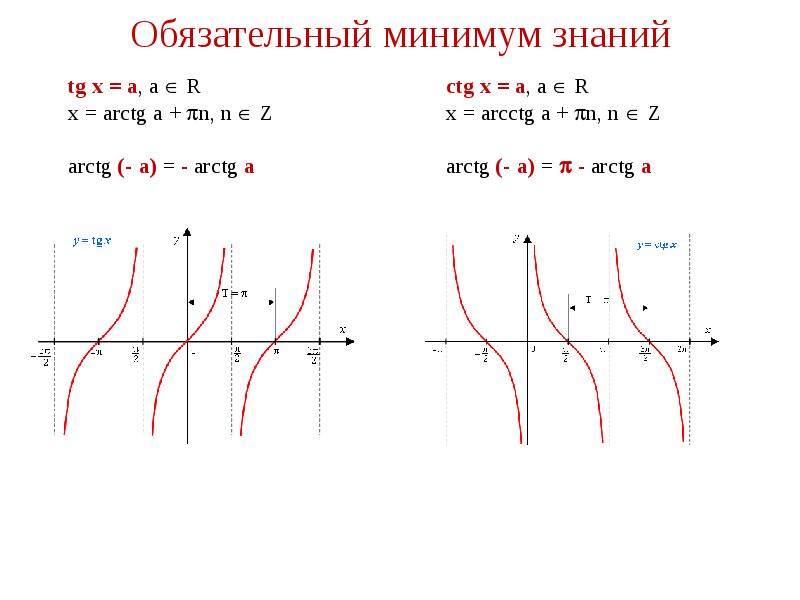
- 4. Обязательный минимум знаний
- 5. Рекомендации по решению тригонометрических уравнений
- 6. Устные упражнения Вычислите arcsin ½ arcsin (- √2/2) arccos
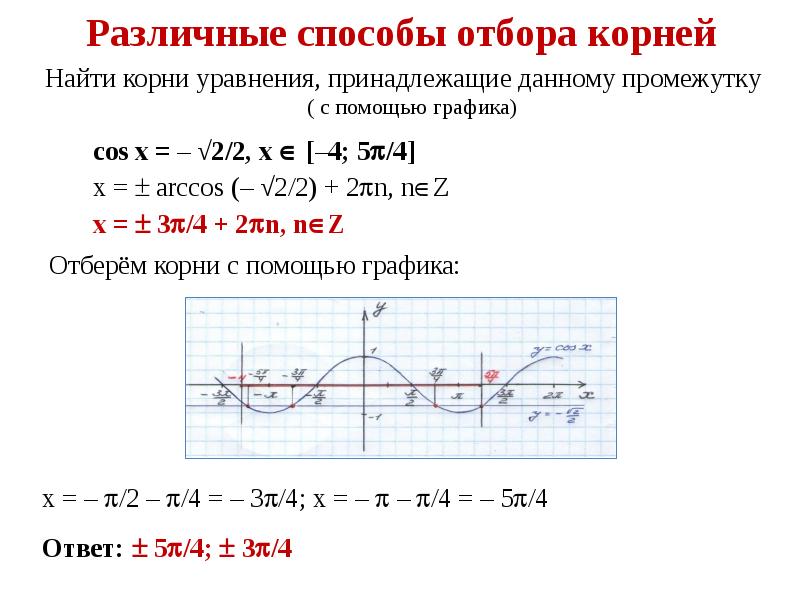
- 7. Различные способы отбора корней
- 8. Различные способы отбора корней
- 9. Различные способы отбора корней
- 10. Различные способы отбора корней
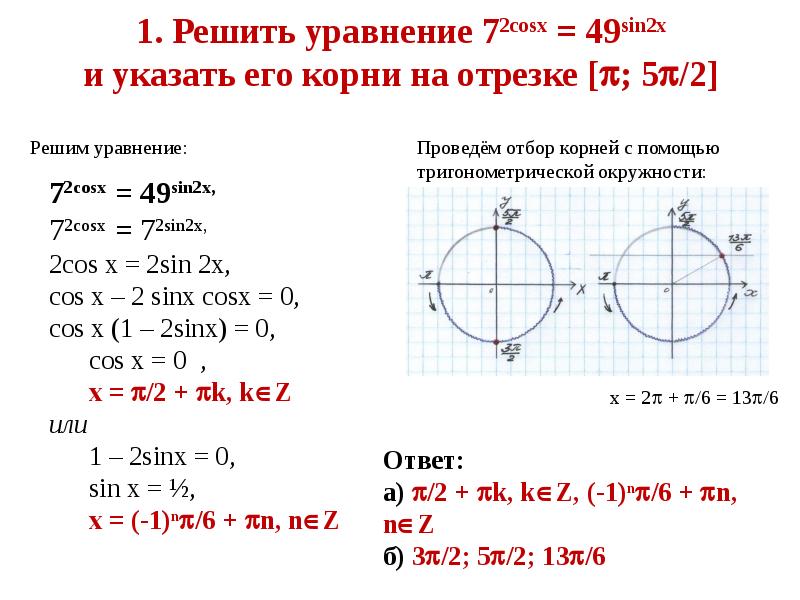
- 11. 1. Решить уравнение 72cosx = 49sin2x и указать его корни на
- 12. 2. Решить уравнение 4cos2 x + 8 cos (x – 3/2)
- 13. Проведем отбор корней на отрезке [3; 92] (с помощью графиков)
- 14. 3. Решить уравнение 4 – cos2 2x = 3 sin2 2x
- 15. Проведём отбор корней на отрезке [0; 1]
- 16. 4. Решить уравнение log5(cos x – sin 2x + 25) =
- 18. 5. Решить уравнение 1/sin2x + 1/sin x = 2 Найти его
- 20. 6. Решить уравнение |sin x|/sin x + 2 = 2cos x
- 21. 7. Решить уравнение 4sin3x=3cos(x- π/2) Найти его корни на промежутке [7/2;
- 22. Объединим решения ( см. рисунок) Уравнение можно решить короче, зная формулу
- 23. Проведём отбор корней на промежутке [7/2; 9/2) х= m/3, mZ. 7/2
- 24. 8. Решить уравнение √1-sin2x= sin x Найти его корни на промежутке
- 25. Проведём отбор корней на отрезке [5/2; 4] x=(-1)k /4 +
- 26. 9. Решить уравнение (sin2x + 2 sin2x)/√-cos x =0 Найти его
- 27. Отберём корни на заданном отрезке Отберём корни на заданном отрезке [-5;
- 28. 10. Решить уравнение 2sin2x =4cos x –sinx+1 Найти его корни на
- 29. Отберём корни с помощью окружности x = /2+2n, nZ, х
- 30. Скачать презентацию








![Проведем отбор корней на отрезке [3; 92] (с помощью графиков) Проведем отбор корней на отрезке [3; 92] (с помощью графиков)](/documents_3/400b3e01a2656329b599786c13153482/img12.jpg)

![Проведём отбор корней на отрезке [0; 1] Проведём отбор корней на отрезке [0; 1]](/documents_3/400b3e01a2656329b599786c13153482/img14.jpg)

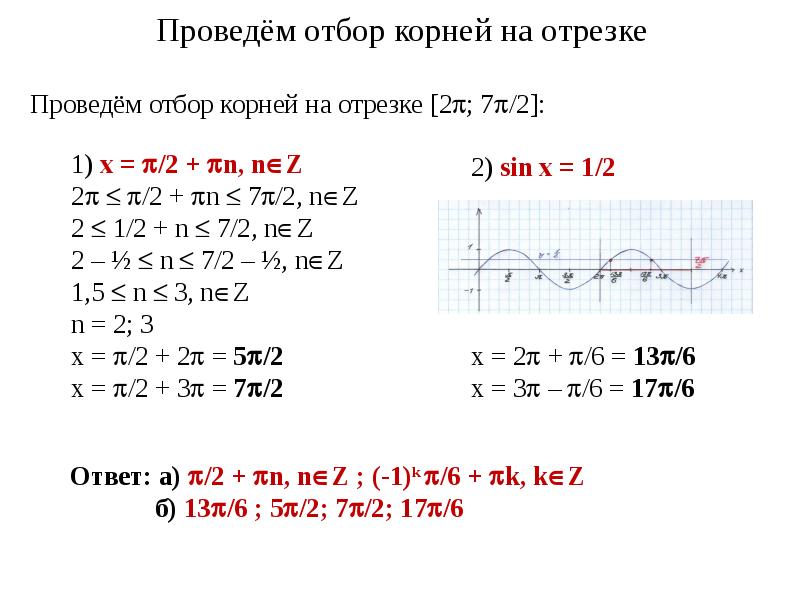







![Проведём отбор корней на отрезке [5/2; 4]
x=(-1)k Проведём отбор корней на отрезке [5/2; 4]
x=(-1)k](/documents_3/400b3e01a2656329b599786c13153482/img24.jpg)




Слайды и текст этой презентации
Скачать презентацию на тему Решение тригонометрических уравнений и способы отбора корней на заданном промежутке можно ниже:
Похожие презентации





























