Случайные величины (лекция 4) презентация
Содержание
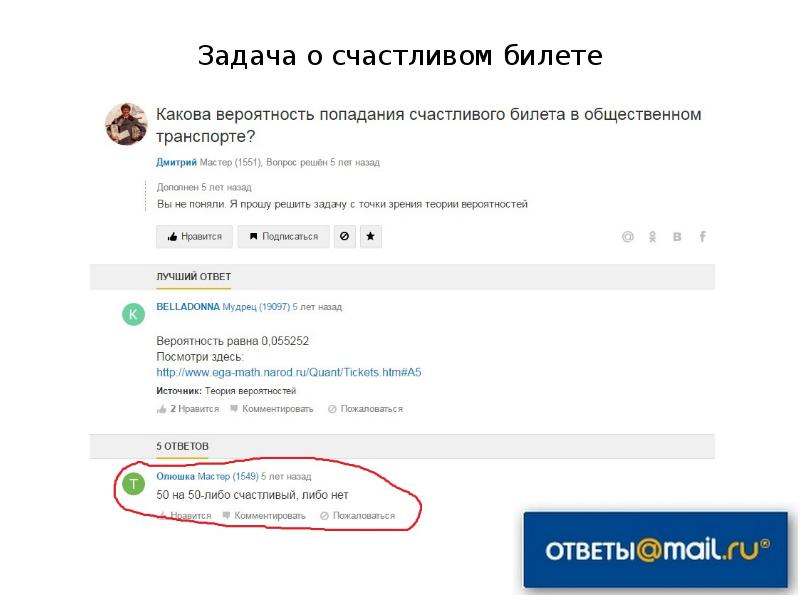
- 2. Задача о счастливом билете
- 4. Зная рекуррентное соотношение и для всех , Зная рекуррентное соотношение
- 5. Числовые характеристики дискретной случайной величины Математическое ожидание Две д.с.в. с
- 6. Формула для вычисления дисперсии Дисперсия равна разности между математическим ожиданием квадрата
- 7. Свойства дисперсии Дисперсия постоянной величины равна 0: Доказательство. Постоянный
- 8. Дисперсия числа появлений событий в независимых испытаниях n независимых испытаний Событие
- 9. Среднее квадратическое отклонение Определение. Среднее квадратическое отклонение случайной величины – это
- 10. От дискретности – к непрерывности! Закон распределения дискретной с.в. можно задать
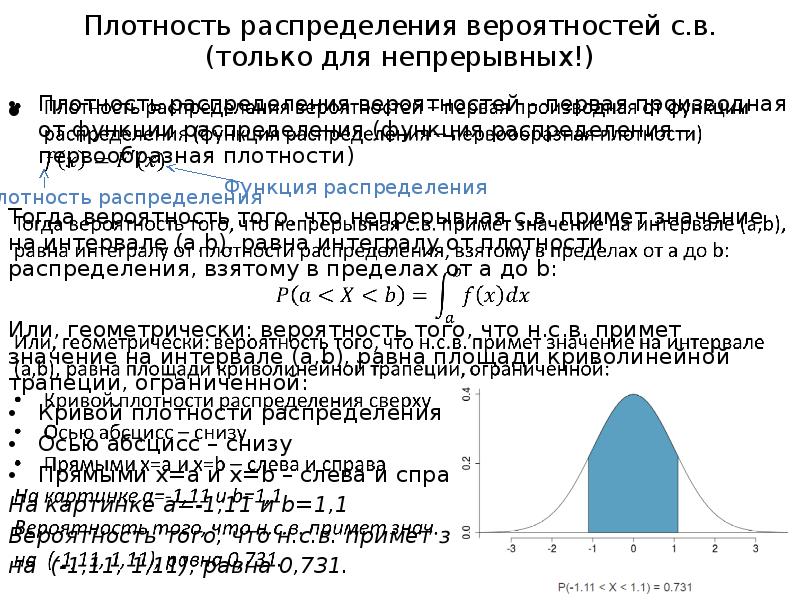
- 11. Плотность распределения вероятностей с.в. (только для непрерывных!) Плотность распределения вероятностей –
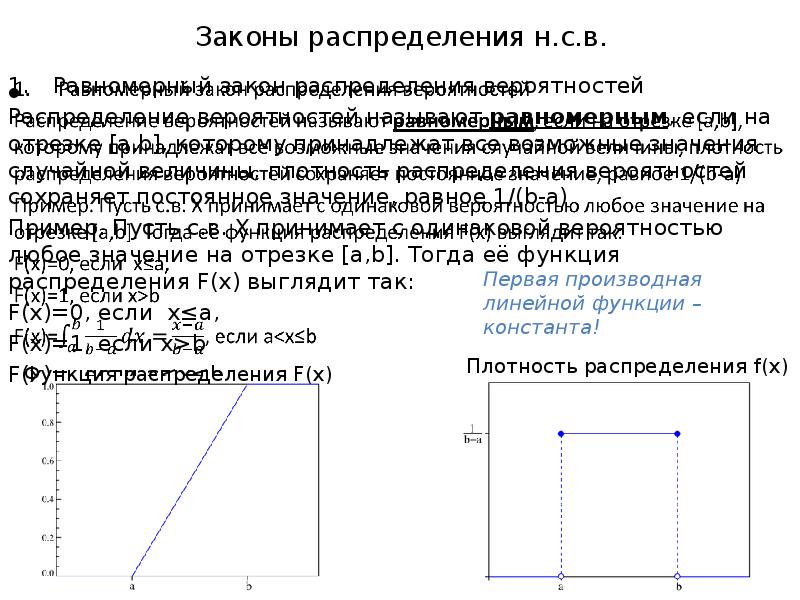
- 12. Законы распределения н.с.в. Равномерный закон распределения вероятностей Распределение вероятностей называют равномерным,
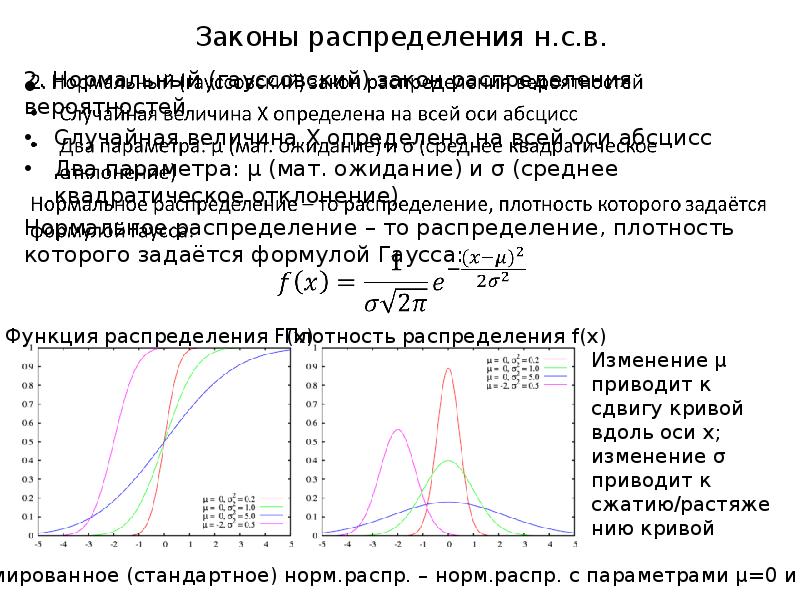
- 13. 2. Нормальный (гауссовский) закон распределения вероятностей 2. Нормальный (гауссовский) закон распределения
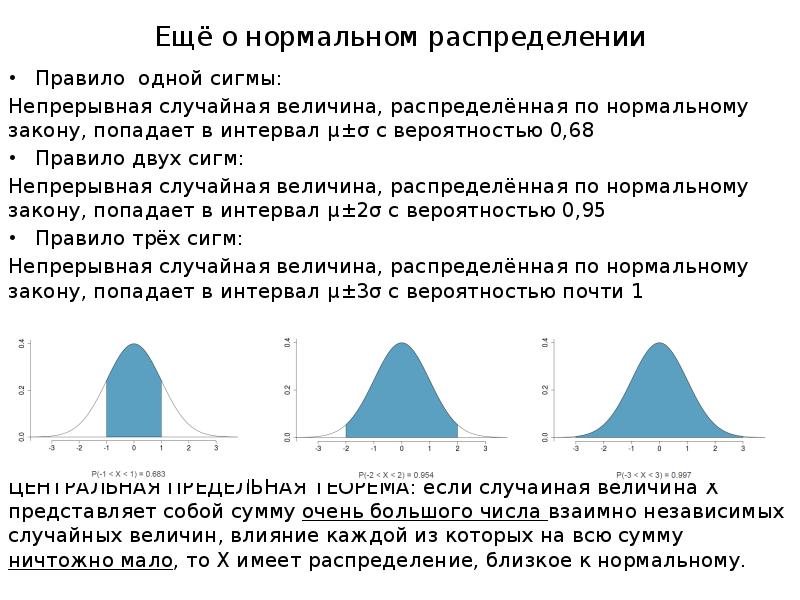
- 14. Ещё о нормальном распределении Правило одной сигмы: Непрерывная случайная величина, распределённая
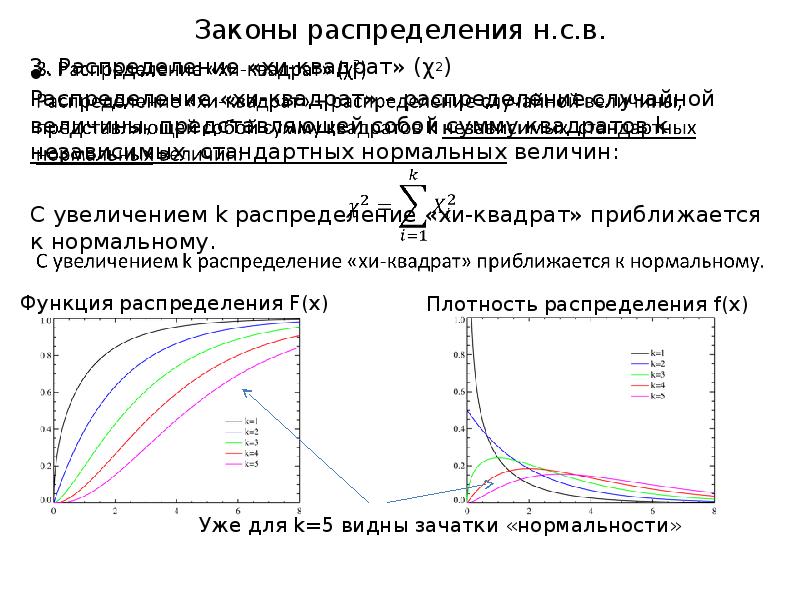
- 15. Законы распределения н.с.в. 3. Распределение «хи-квадрат» (χ2) Распределение «хи-квадрат» – распределение
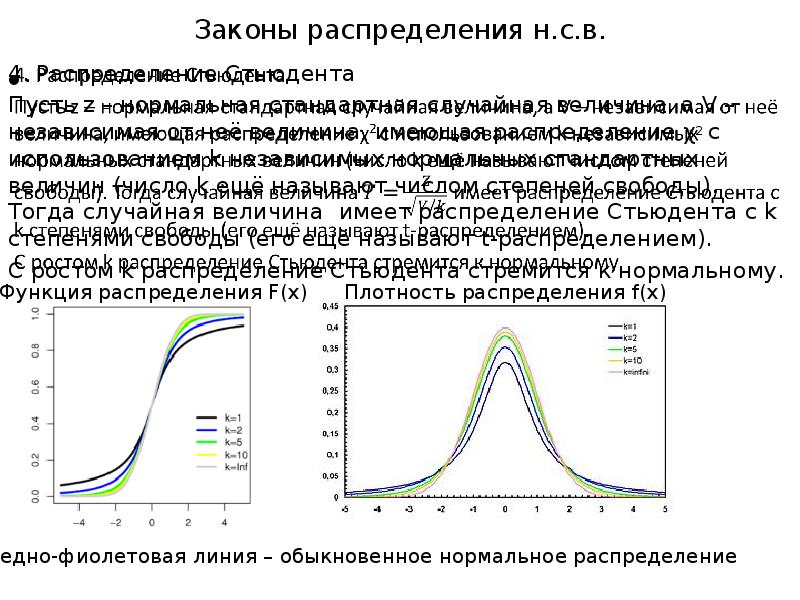
- 16. Законы распределения н.с.в. 4. Распределение Стьюдента Пусть z – нормальная стандартная
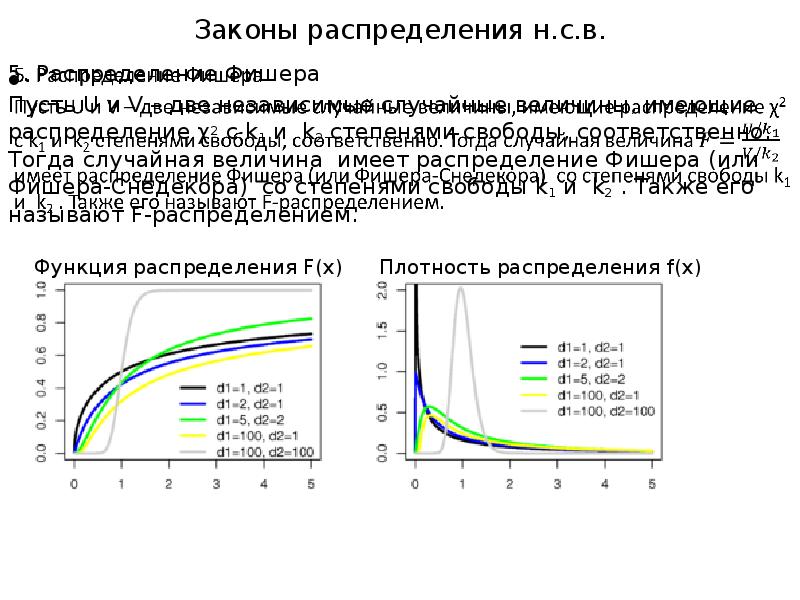
- 17. 5. Распределение Фишера 5. Распределение Фишера Пусть U и V –
- 18. Резюме - определение дисперсии д.с.в. - удобная формула для вычисления дисперсии
- 19. Скачать презентацию










Слайды и текст этой презентации
Похожие презентации





























