Стационарное свободное двумерное течение жидкости внутри двугранного угла с движущимися стенками презентация
Содержание
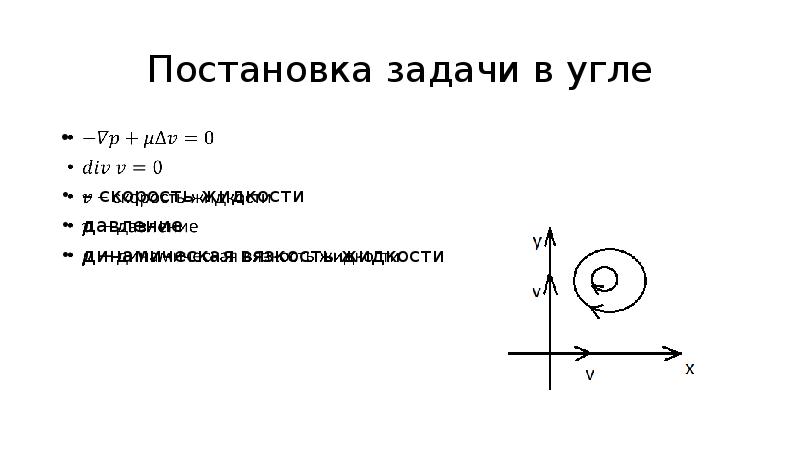
- 2. Постановка задачи в угле – скорость жидкости давление динамическая вязкость жидкости
- 3. Рассматриваем стационарное свободное двумерное течение жидкости внутри двугранного угла с движущимися
- 4. Имеем следующие граничные условия для компонент скоростей на границах угла :
- 5. Функция тока Введем функцию тока определяемую уравнениями Основным удобством введения
- 6. Общее решение бигармонического уравнения Вводим комплексные переменные где мнимая единица Оператор
- 7. где произвольная голоморфная функция. Отсюда следует, что общим решением уравнения (12)
- 8. Пример 1 Зададим следующие функции, которые не имеют особенностей в области
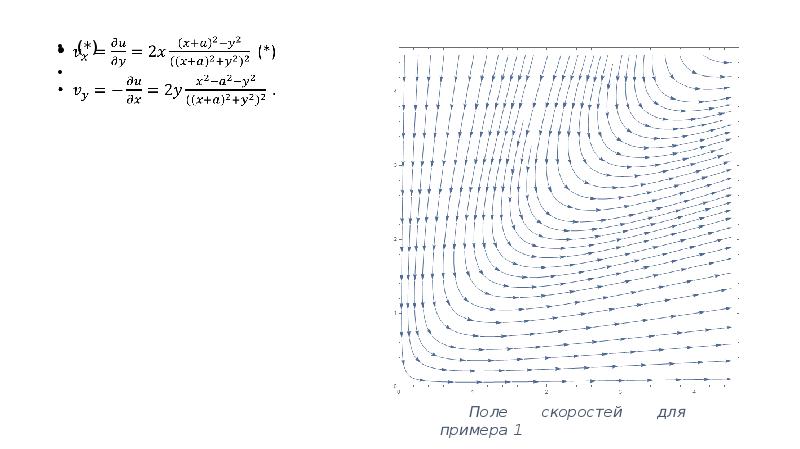
- 9. (*) (*)
- 10. На рисунке 1. приведена картина течения (иными словами линии тока), соответствующая
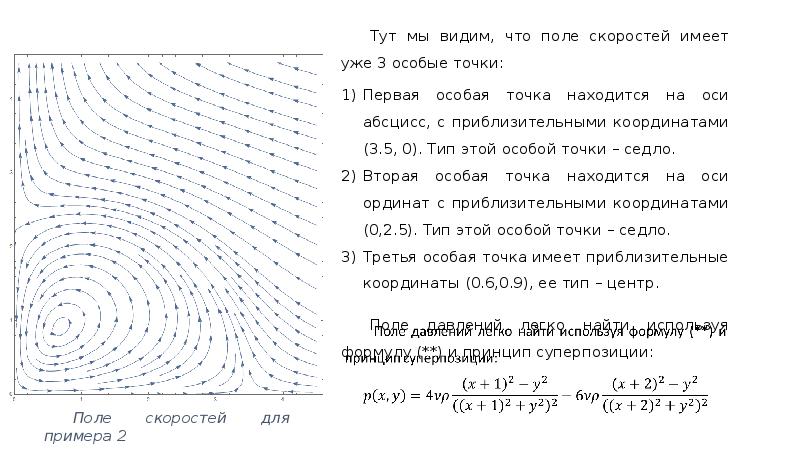
- 11. Пример 2 . Рассмотрим функцию тока Соответствующее поле скоростей дается
- 13. Пример 3 Рассмотрим случай . Функция тока Соответствующее поле скоростей дается
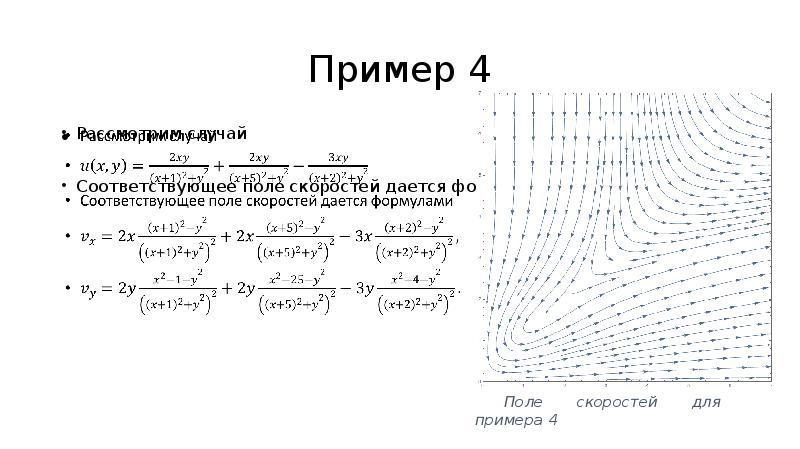
- 14. Пример 4 Рассмотрим случай Соответствующее поле скоростей дается формулами
- 15. Пример 5 Прежде чем мы перейдем к рассмотрению новых примеров следует
- 16. Положим Положим Эти функции аналитичны в верхней полуплоскости так как при
- 19. Список литературы. 1. Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Гидродинамика.
- 20. Скачать презентацию















Слайды и текст этой презентации
Скачать презентацию на тему Стационарное свободное двумерное течение жидкости внутри двугранного угла с движущимися стенками можно ниже:
Похожие презентации