Тема проекта: «Максимум удовольствия, оптимизация затрат» презентация
Содержание



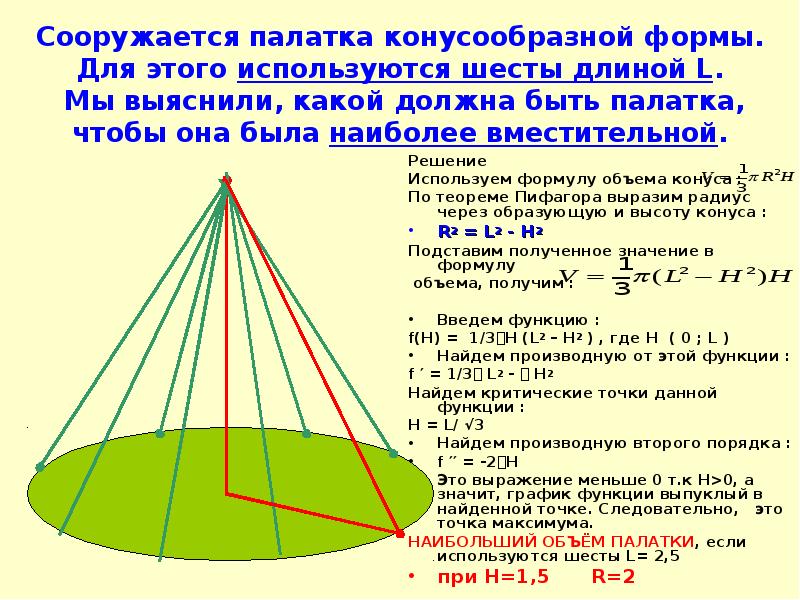




Слайды и текст этой презентации
Скачать презентацию на тему Тема проекта: «Максимум удовольствия, оптимизация затрат» можно ниже:
Похожие презентации





























