Теория графов. Определения и примеры. Пути и циклы презентация
Содержание
- 2. Определения и примеры Хотя обычно теорию графов считают одной из современных
- 3. Определения и примеры Эйлер (1707 – 1783) родился в Швейцарии и
- 4. Определения и примеры Как и большинство выдающихся математиков того времени, Эйлер
- 5. Определения и примеры Что такое ‘граф’? Интуитивно, граф – это
- 6. Определения и примеры Определение 1 Неориентированный граф (или просто граф) состоит
- 7. Определения и примеры Определение 1 Граф называется простым, если в нем
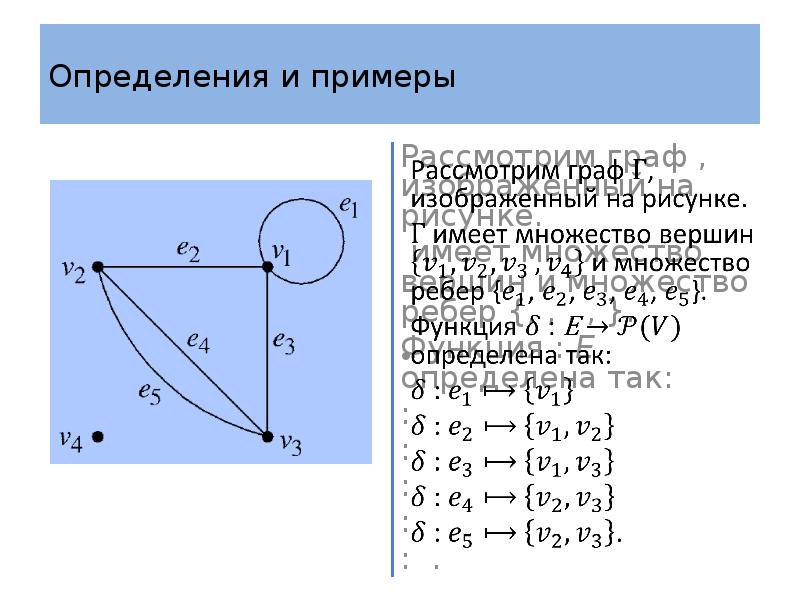
- 8. Определения и примеры
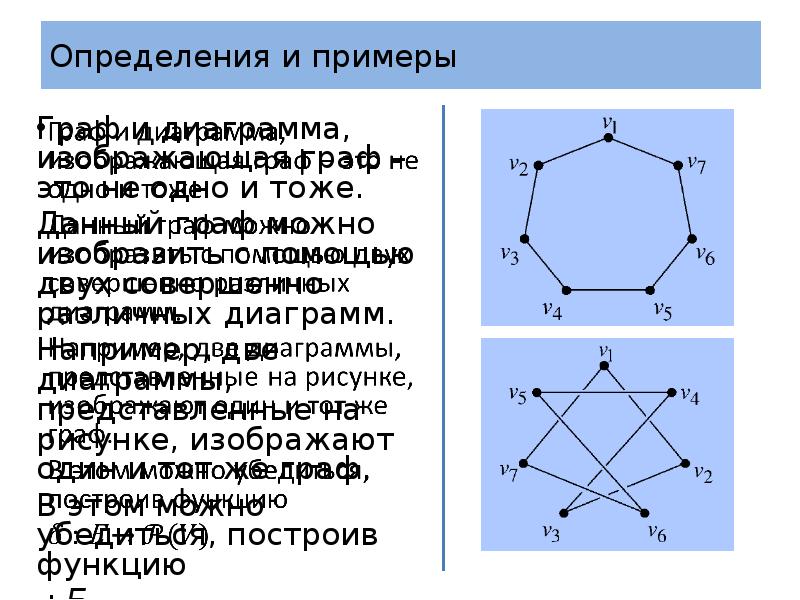
- 9. Определения и примеры Граф и диаграмма, изображающая граф – это не
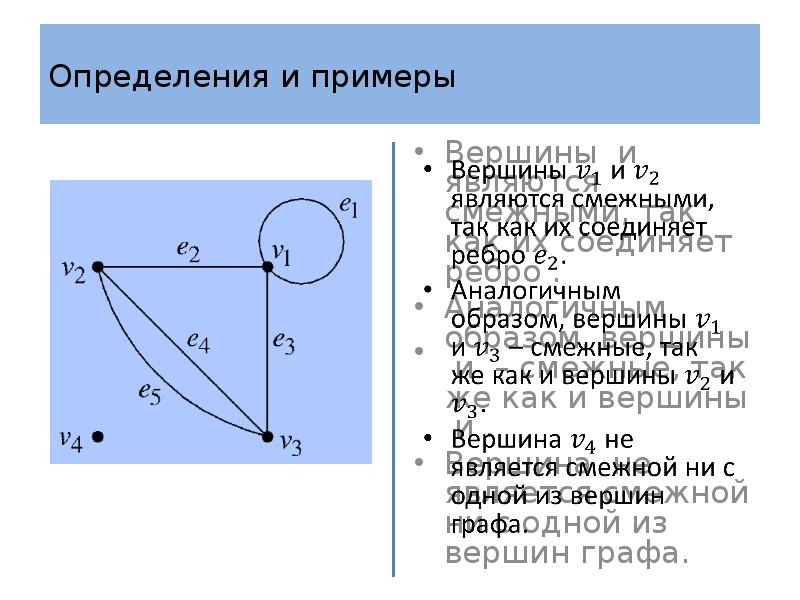
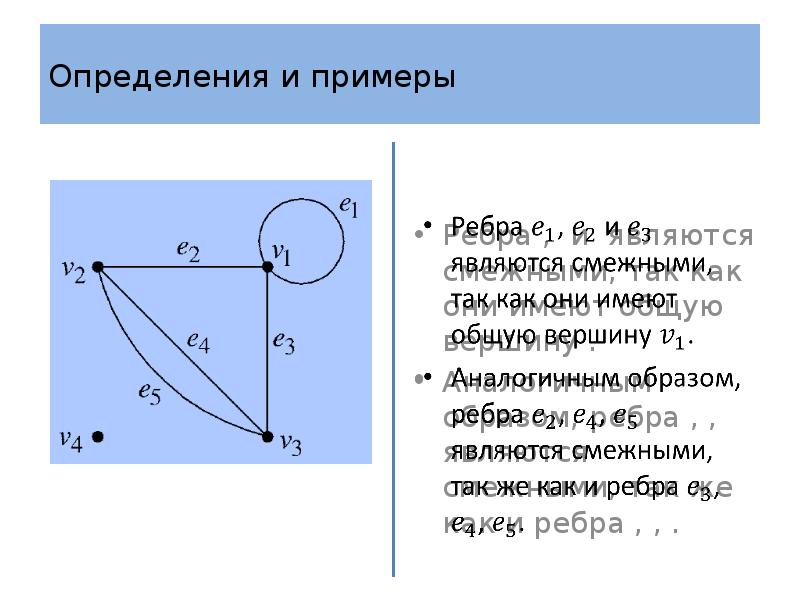
- 10. Определения и примеры Определение 2 Вершины и называются смежными, если существует
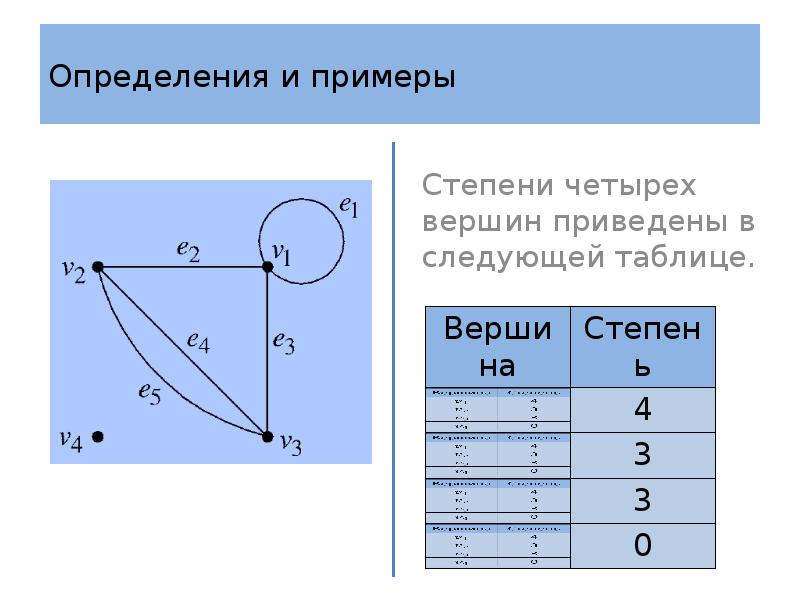
- 11. Определения и примеры Определение 2 Степень или валентность, deg(), вершины –
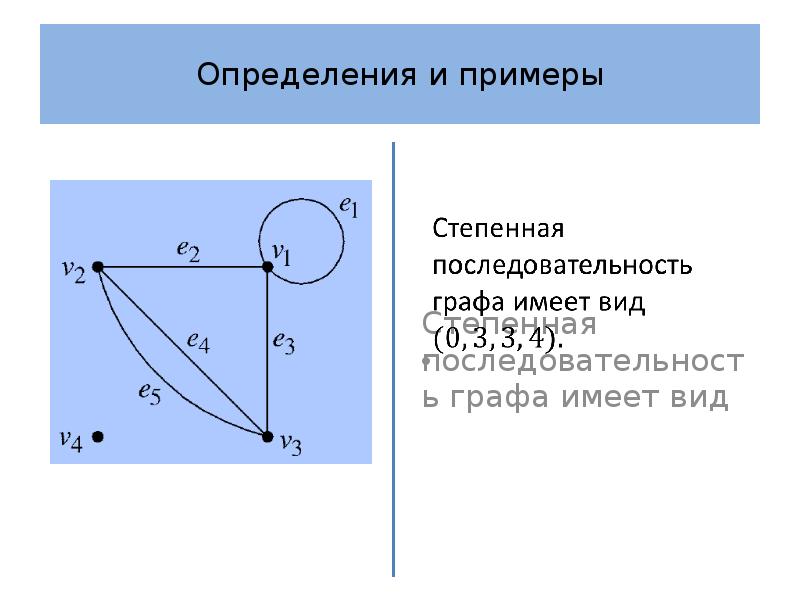
- 12. Определения и примеры Определение 2 Степенная последовательность графа – это последовательность
- 13. Определения и примеры
- 14. Определения и примеры
- 15. Определения и примеры
- 16. Определения и примеры
- 17. Определения и примеры
- 18. Определения и примеры Определение 3 Нулевым графом (или вполне несвязным графом)
- 19. Определения и примеры Определение 3 Двудольным графом называется граф, для множества
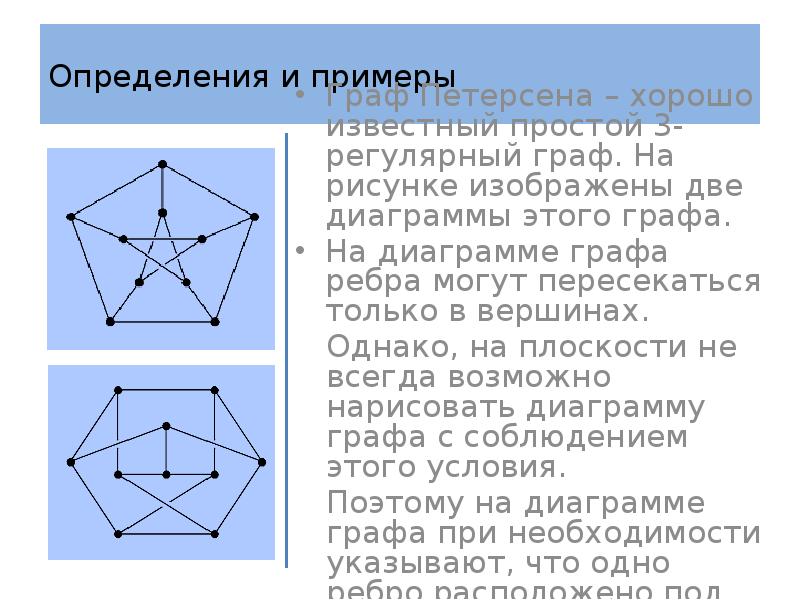
- 20. Определения и примеры Примеры Так как полный граф является простым, то
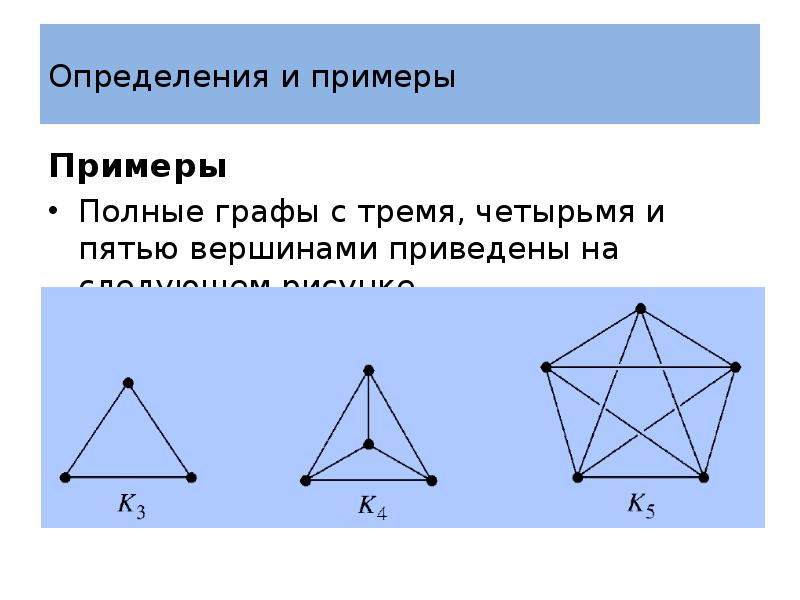
- 21. Определения и примеры Примеры Полный граф с вершинами можно описать следующим
- 22. Определения и примеры Примеры Полные графы с тремя, четырьмя и пятью
- 23. Определения и примеры Примеры Пусть – двудольный граф, для множества вершин
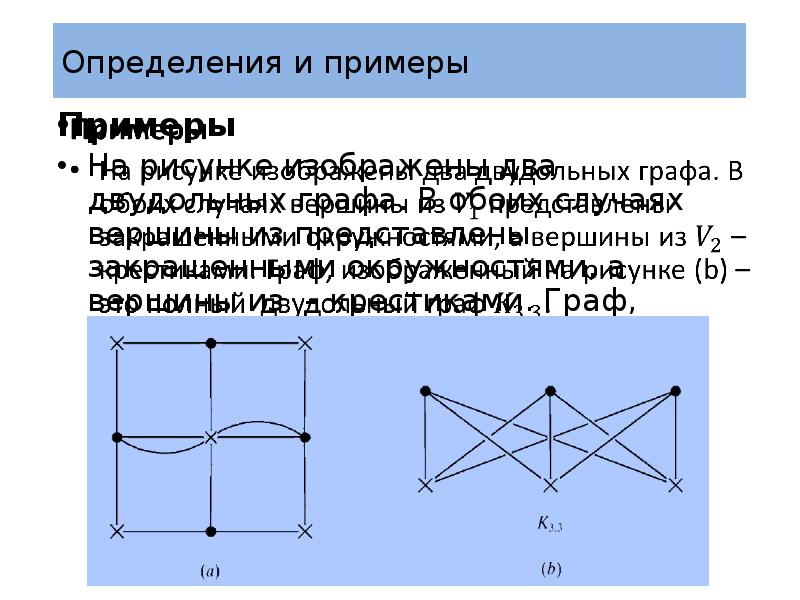
- 24. Определения и примеры Примеры Полный двудольный граф полностью специфицируется числами и
- 25. Определения и примеры Примеры На рисунке изображены два двудольных графа. В
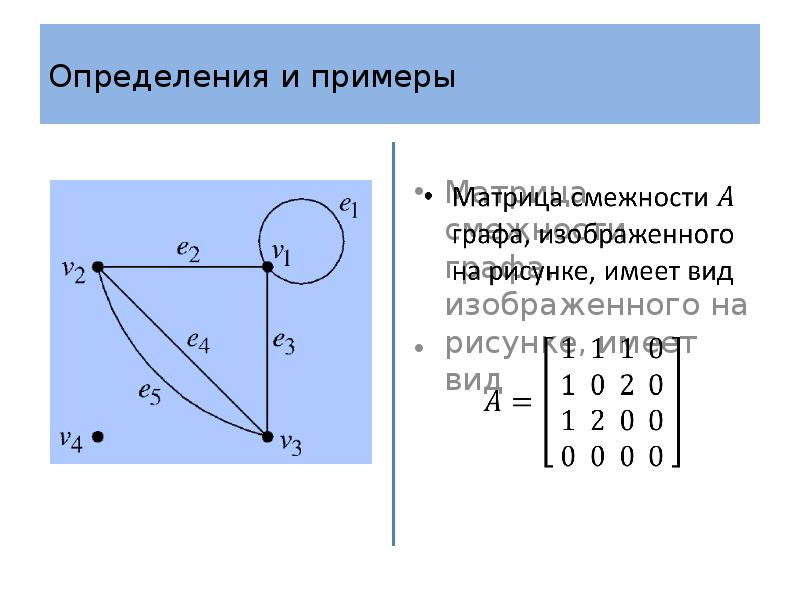
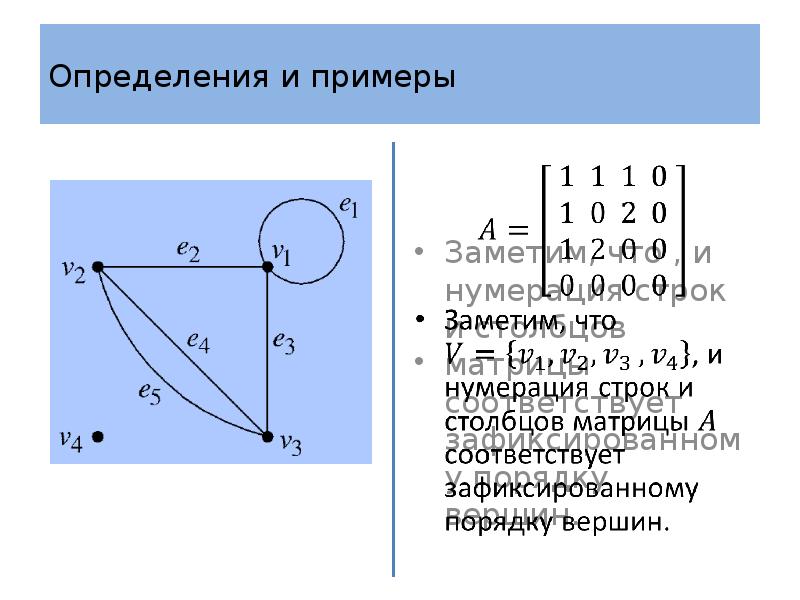
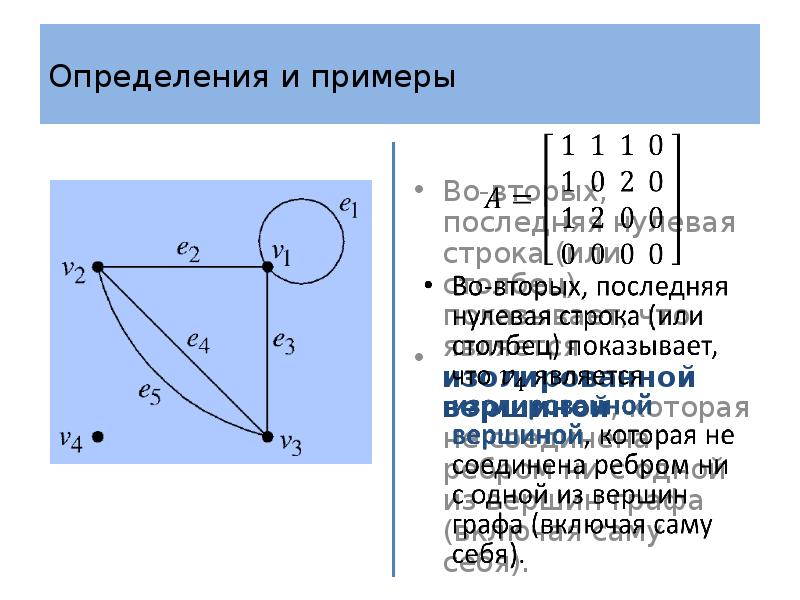
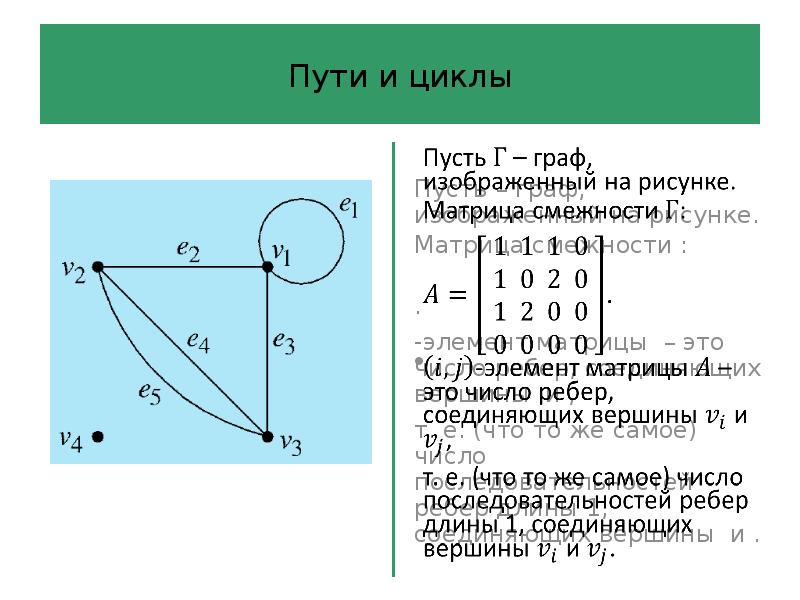
- 26. Определения и примеры Определение 4 Пусть – граф с множеством вершин
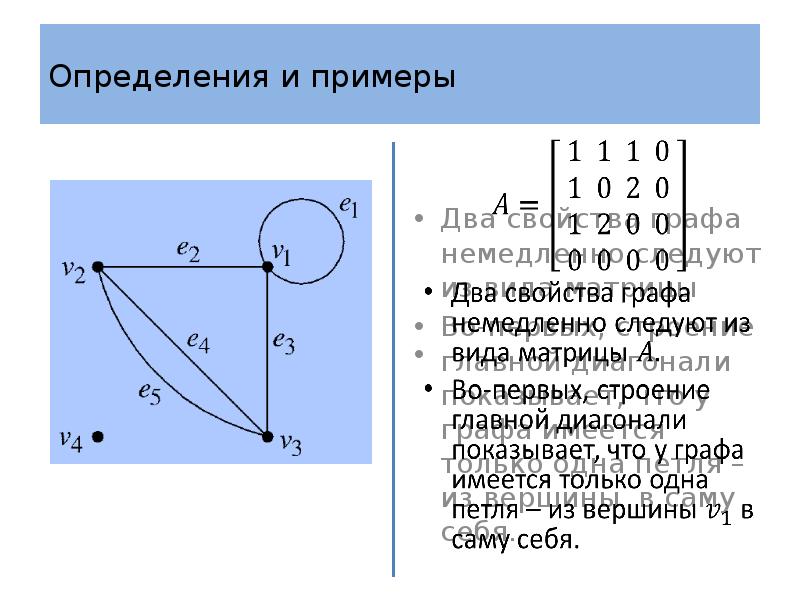
- 27. Определения и примеры Матрица смежности симметрична, так как число ребер, соединяющих
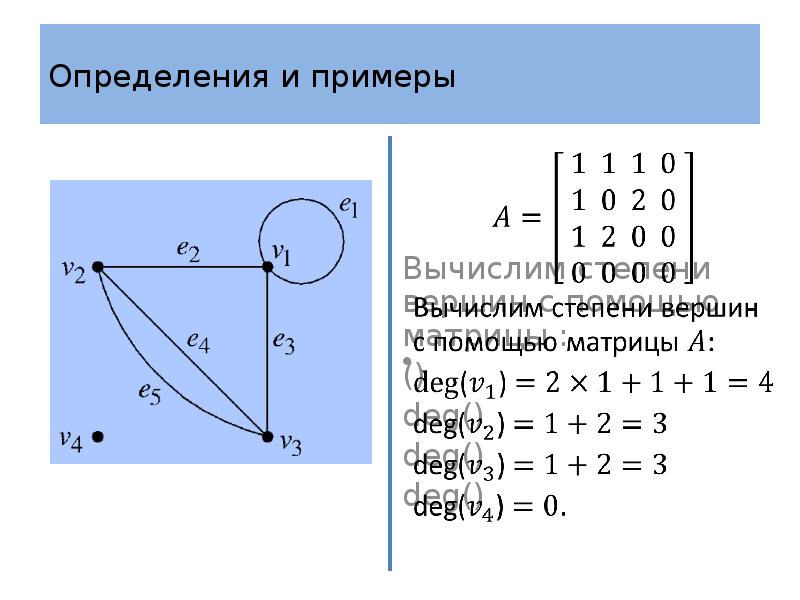
- 28. Определения и примеры Степень вершины легко определить с помощью матрицы смежности.
- 29. Определения и примеры
- 30. Определения и примеры
- 31. Определения и примеры
- 32. Определения и примеры
- 33. Определения и примеры
- 34. Определения и примеры Примеры Матрица смежности нулевого графа с вершинами –
- 35. Определения и примеры Примеры Матрица смежности полного графа – матрица с
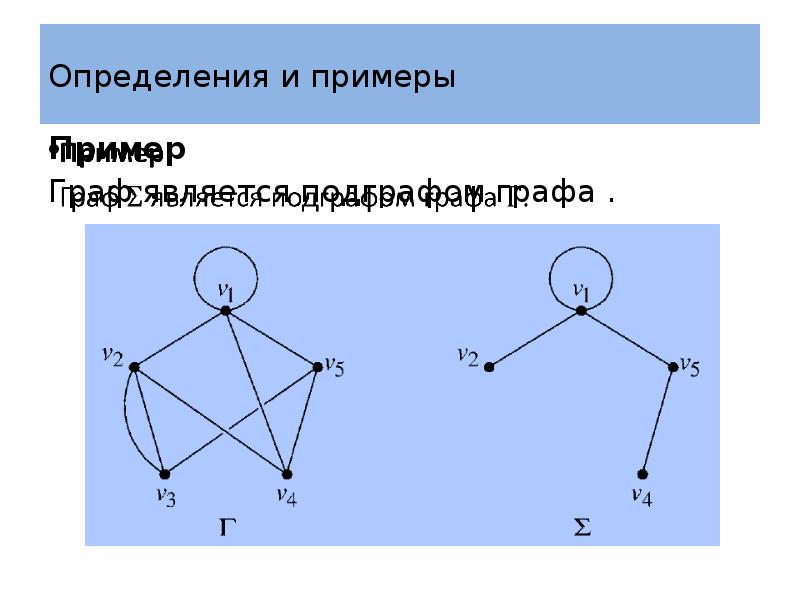
- 36. Определения и примеры Определение 5 Граф называют подграфом графа и пишут:
- 37. Определения и примеры Условие: для каждого ребра из – означает, что
- 38. Определения и примеры Пример Граф является подграфом графа .
- 39. Пути и циклы По аналогии с дорожной картой мы можем рассматривать
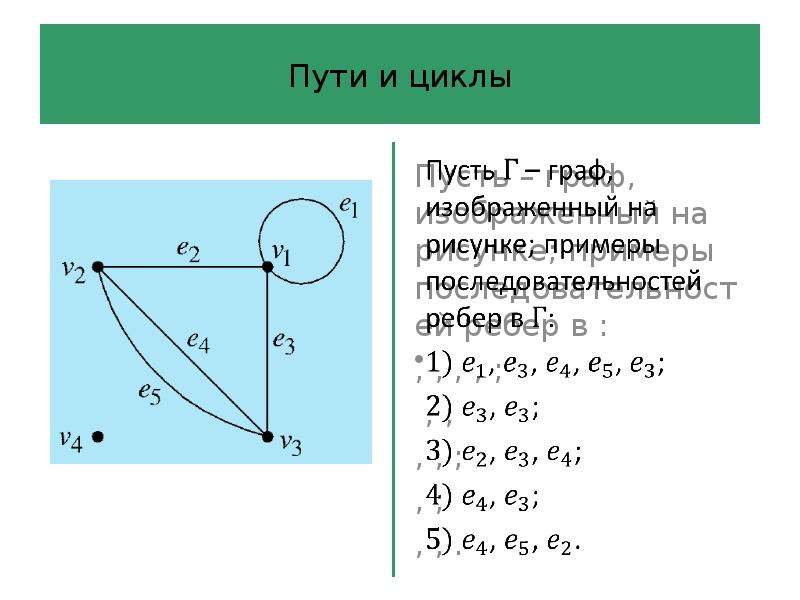
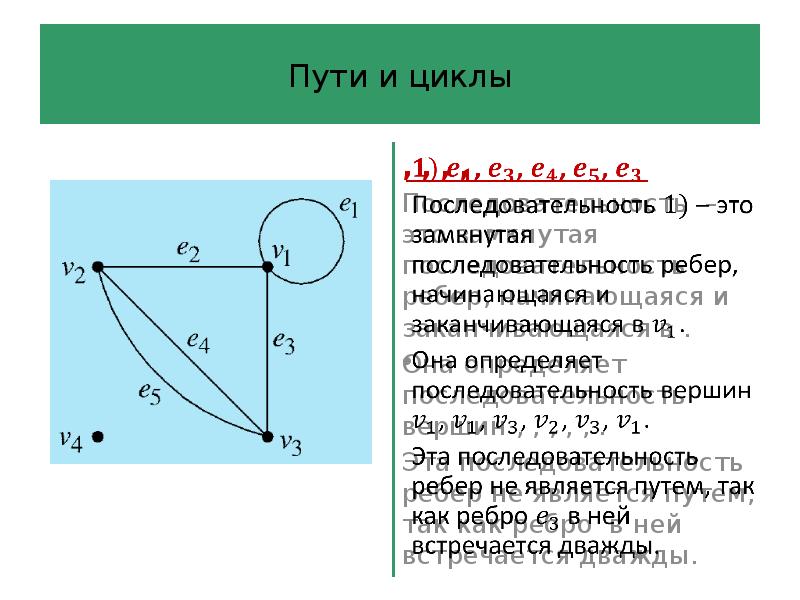
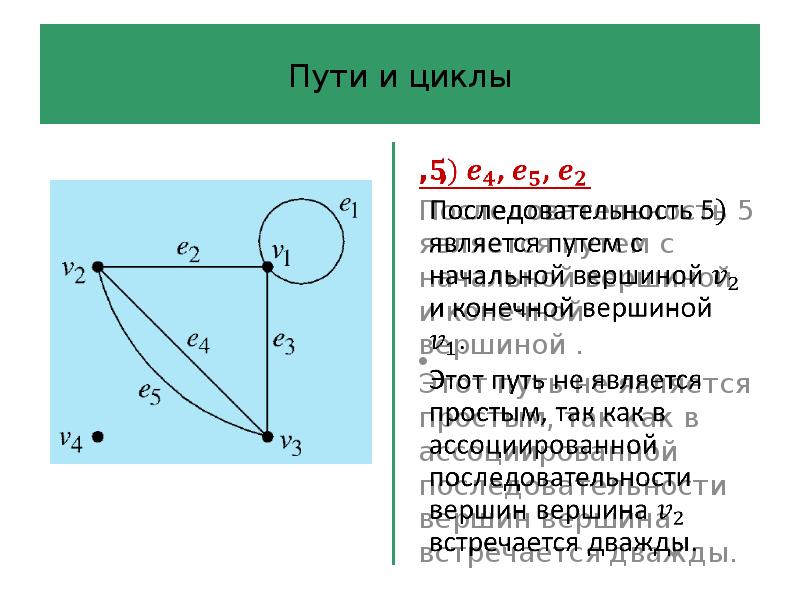
- 40. Пути и циклы Определение 6 Последовательность ребер длины в графе –
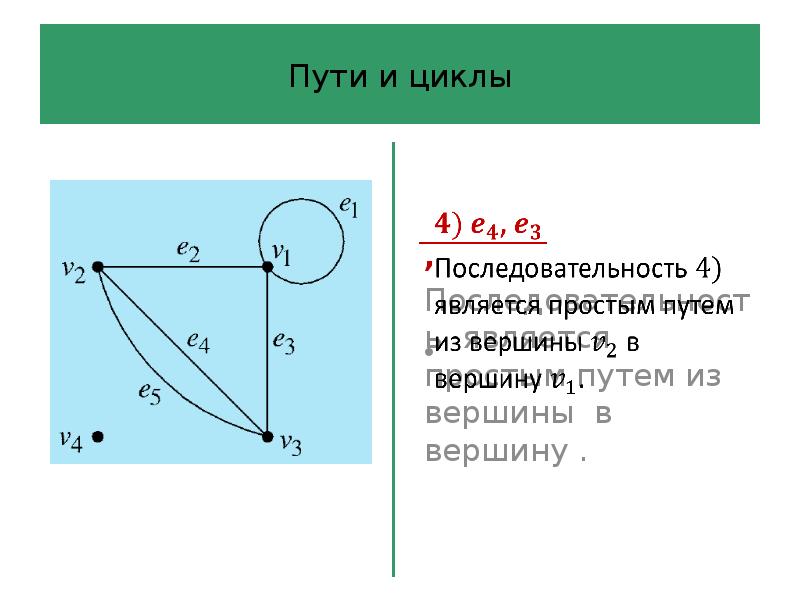
- 41. Пути и циклы Определение 6 Путь – это последовательность ребер, в
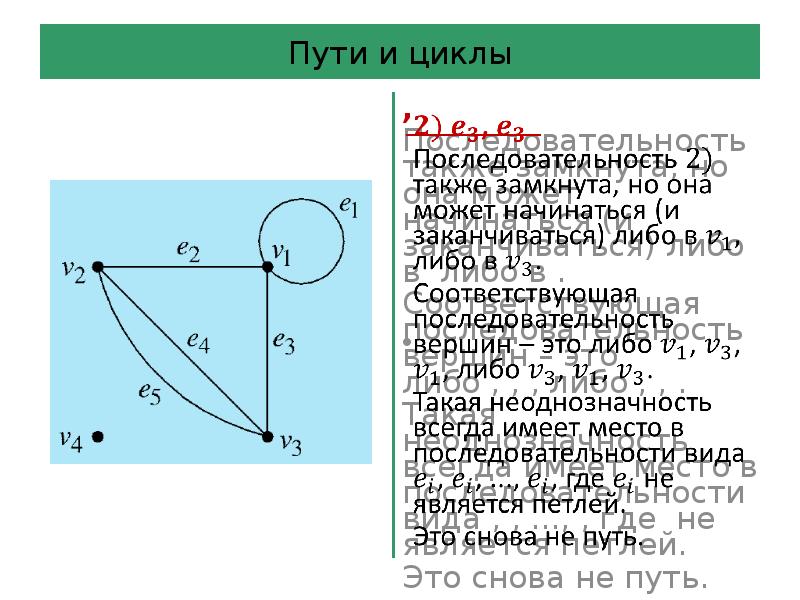
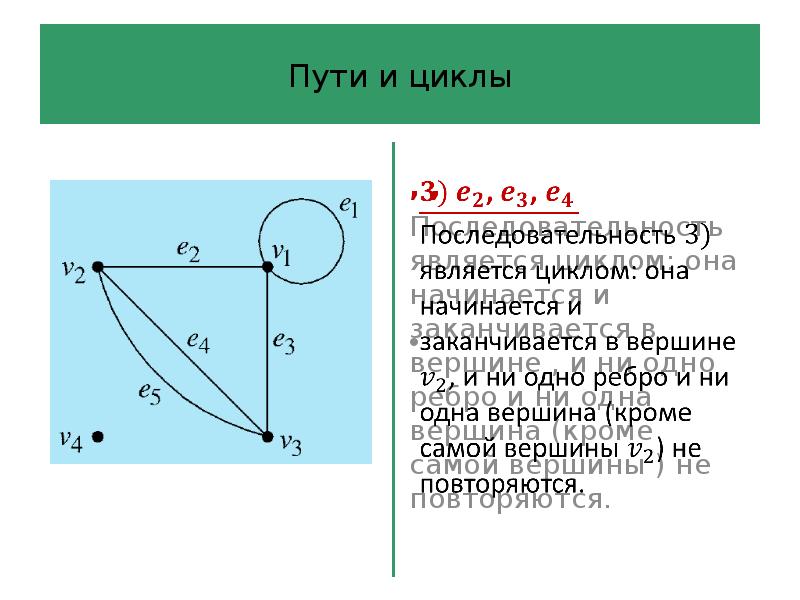
- 42. Пути и циклы Последовательность ребер графа – это произвольная последовательность ребер,
- 43. Пути и циклы
- 44. Пути и циклы
- 45. Пути и циклы
- 46. Пути и циклы
- 47. Пути и циклы
- 48. Пути и циклы
- 49. Пути и циклы
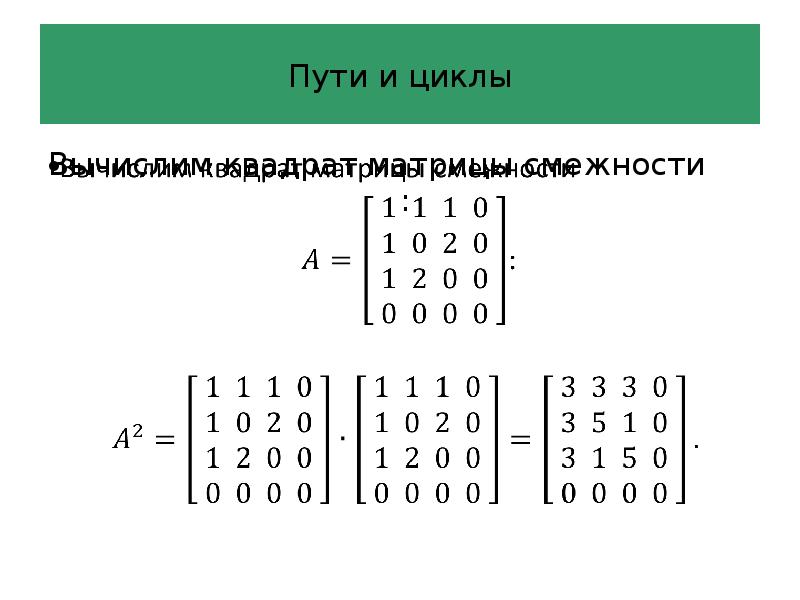
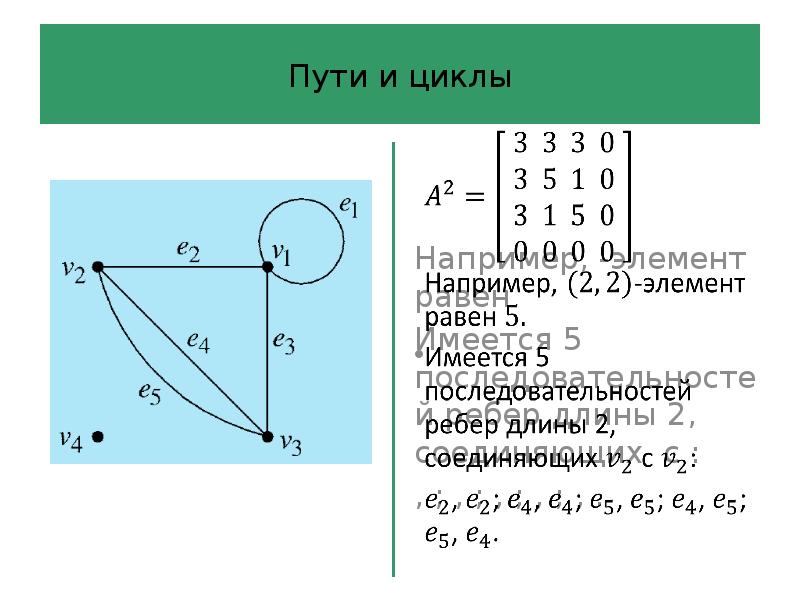
- 50. Пути и циклы Вычислим квадрат матрицы смежности :
- 51. Пути и циклы
- 52. Пути и циклы
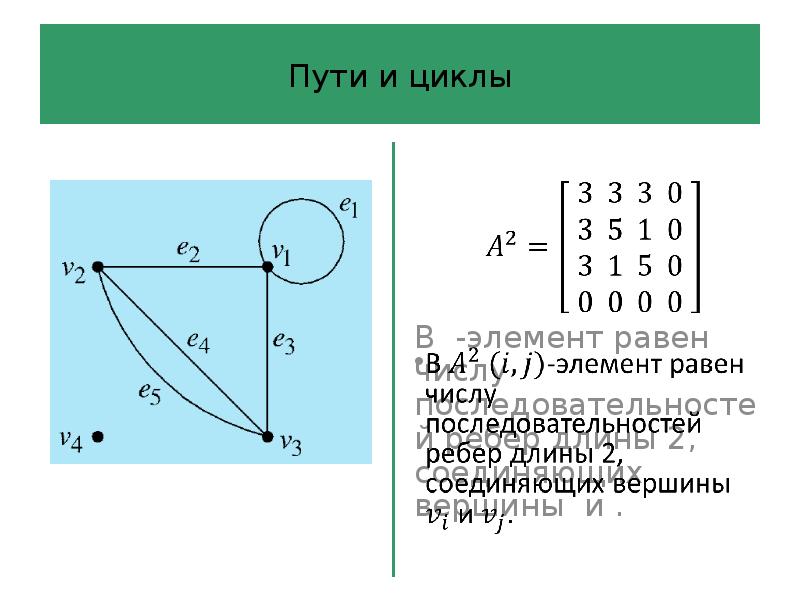
- 53. ? В матрице -элемент равен числу последователь-ностей ребер длины , соединяющих
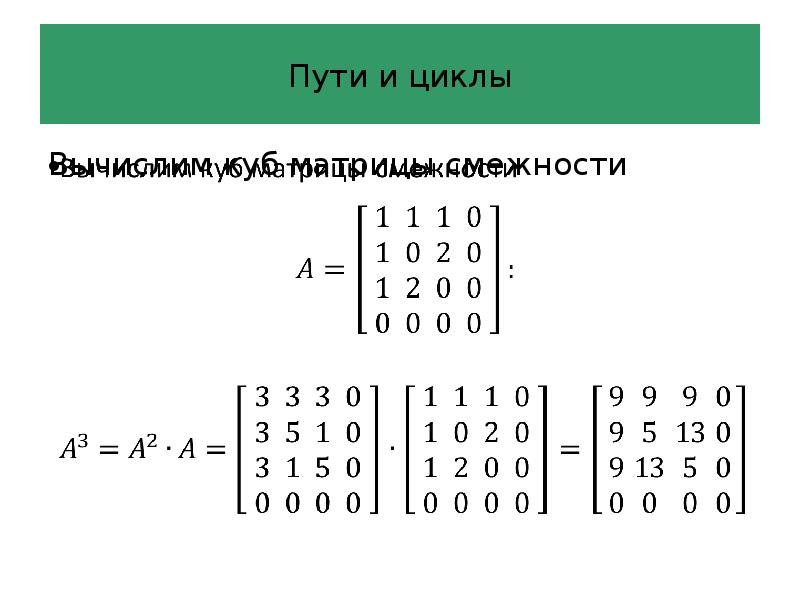
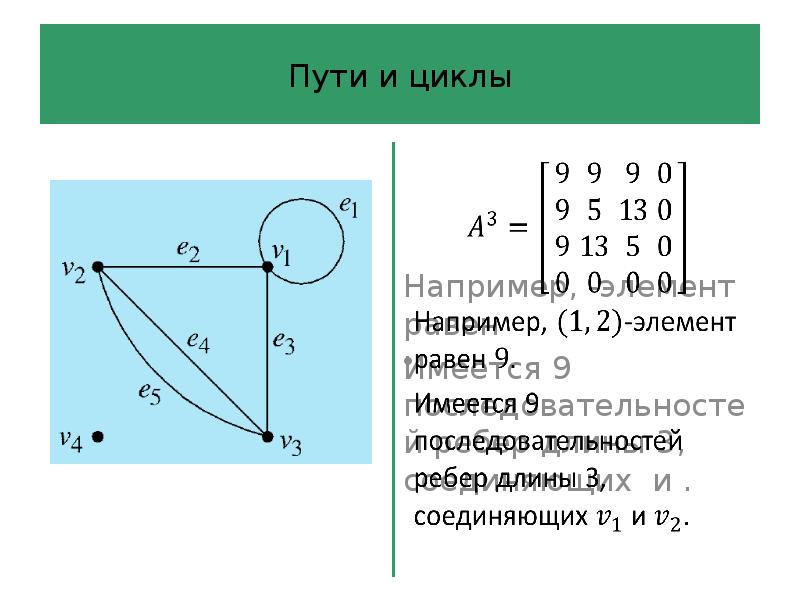
- 54. Пути и циклы Вычислим куб матрицы смежности
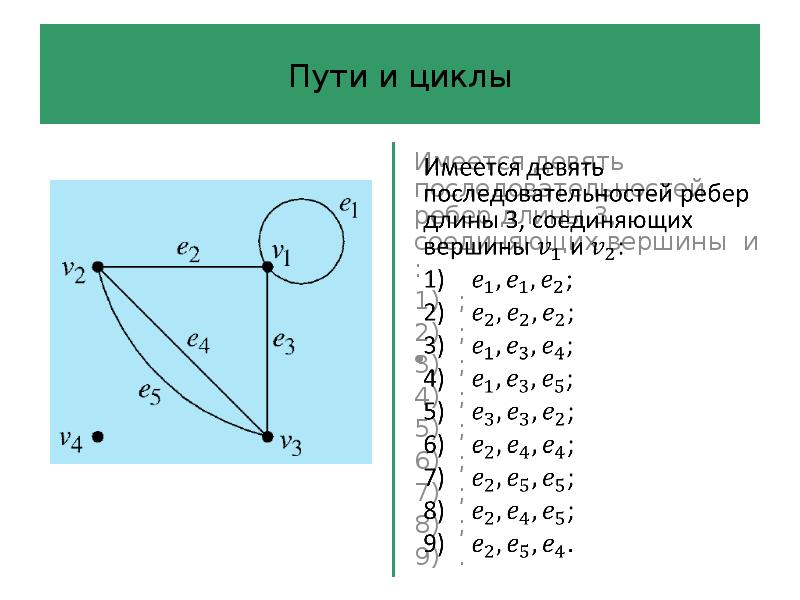
- 55. Пути и циклы
- 56. Пути и циклы
- 57. Пути и циклы Теорема 1 Пусть – граф с множеством вершин
- 58. Пути и циклы На интуитивном уровне ясно, что некоторые графы являются
- 59. Пути и циклы Определение 7 Граф называется связным, если для любых
- 60. Пути и циклы Произвольный граф разбивается на несколько связных подграфов, называемых
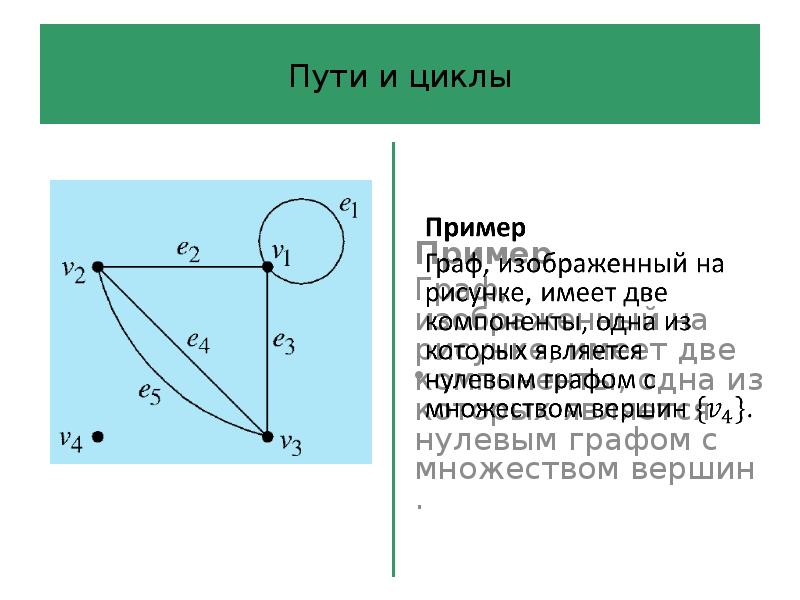
- 61. Пути и циклы Компоненты графа – это его связные ‘куски’. В
- 62. Пути и циклы Имеется альтернативный способ определения компонент графа .
- 63. Пути и циклы тогда и только тогда, когда и можно соединить
- 64. Пути и циклы Единственная трудность состоит в доказательстве транзитивности отношения .
- 65. Пути и циклы тогда и только тогда, когда и можно соединить
- 66. Пути и циклы
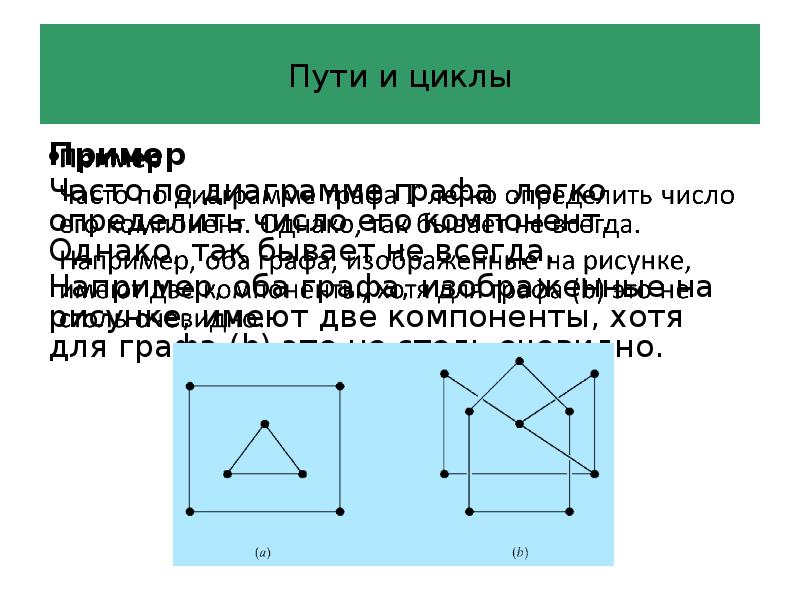
- 67. Пути и циклы Пример Часто по диаграмме графа легко определить
- 68. Скачать презентацию





































Слайды и текст этой презентации
Скачать презентацию на тему Теория графов. Определения и примеры. Пути и циклы можно ниже:
Похожие презентации





























