Теория кодирования презентация

Теория кодирования Ирина Борисовна Просвирнина Коды, примеры кодов Порождающие матрицы Смежные классы группы по подгруппе, теорема Лагранжа Декодирование по лидеру смежного класса Декодирование по лидеру смежного класса с использованием синдромов Коды Хемминга

Коды Определим код как представление множества символов строками, состоящими из единиц и нулей. Это множество символов обычно включает буквы алфавита, цифры и, как правило, определенные контрольные символы. Коды представляются бинарными строками с целью использования их компьютерами для хранения и передачи данных.

Коды Желательно, чтобы коды обладали некоторыми свойствами. Наиболее важное свойство кода состоит в том, что когда сообщение кодируется как двоичная строка, состоящая из конкатенации элементов кода, эта конкатенация однозначна. При декодировании сообщения не должно возникать проблем с тем, какую букву представляет элемент кода. Такой код назовем однозначно декодируемым кодом.

Коды Существует несколько способов достижения этой цели. Один из них – кодирование всех символов двоичными строками одной длины. Такой код называется блоковым. Например, если для кодирования каждого символа используется 8 бит, то известно, что каждые восемь бит представляют один символ передаваемого сообщения. Блоковый код особенно полезен при ограничении длины кода для каждого посланного символа или буквы.

Коды Другим способом построения однозначно декодируемого кода является использование префиксного кода. Код является префиксным, если обладает тем свойством, что элемент кода не может быть начальной строкой другого элемента кода. Таким образом, при чтении строки из единиц и нулей, изображающей символ , всегда известен момент завершения строки. Префиксный код называют также мгновенным кодом.

Коды Разновидностью префиксного кода является кома-код. При его использовании каждый символ кодируется строкой из единиц, в конце которой стоит нуль. Значит, множество строк кода имеет вид Этот код имеет явный недостаток: элементы кода могут быть очень длинными и занимать большой объем памяти.

Коды Часто необходимо сжимать данные, чтобы минимизировать объем памяти для их хранения или время для передачи данных. Что касается минимизации объема памяти, то наиболее эффективным является код Хаффмана. Преимущество кода Хаффмана состоит также в том, что это мгновенный код. Хорошо известным примером кода, минимизирующего время передачи, является код Морзе.

Коды В кодах Хаффмана и Морзе буквы или символы, которые встречаются наиболее часто, имеют более короткий код.

Коды В коде Морзе буквы разделены "пробелами", а слова – тремя "пробелами". В данном случае "пробелы" – это единицы времени.

Коды В процессе передачи данных могут возникать ошибки. Все, что может стать причиной ошибок, называется неопределенным термином "шум". Например, данные, полученные от отдаленного космического корабля, наверняка подвержены различного рода шумам.

Коды В некоторых случаях интерес представляет только определение наличия ошибки, что соответствует ситуации передачи данных еще раз. Коды, обладающие свойством определения наличия ошибок, называются кодами, обнаруживающими ошибки.

Коды В другом случае, когда данные не могут быть переданы еще раз (например, данные от удаленного космического корабля), требуется дополнительная информация о данных с целью не только обнаружения, но и исправления ошибки. Коды, позволяющие исправлять ошибки, называются кодами, исправляющими ошибки.

Коды Может показаться разумным всегда использовать коды с исправлением ошибок. Проблема использования кодов с исправлением ошибок и кодов с обнаружением ошибок состоит в том, что они должны включать в себя дополнительную информацию, поэтому они являются менее эффективными в отношении минимизации объема памяти.

Коды К сожалению, использование кодов с исправлением ошибок и кодов с обнаружением ошибок не дает абсолютной гарантии того, что ошибка будет исправлена или обнаружена.

Коды В качестве первого метода обнаружения ошибок рассмотрим бит контроля четности. Продемонстрируем этот метод на примере кода ASCII.

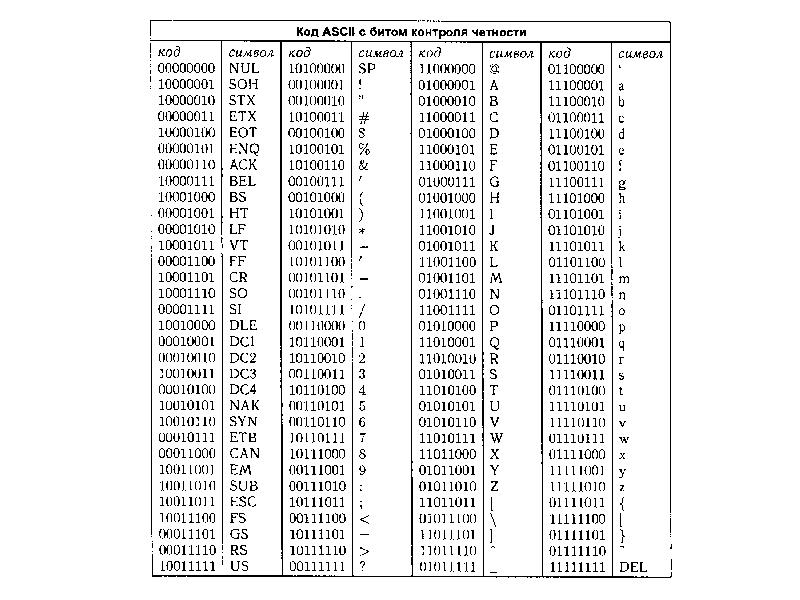
Коды ASCII-код является блоковым кодом, который использует 7 битов, поэтому любой закодированный символ изображается строкой из семи символов 1 и 0. Восьмой бит добавляется таким образом, чтобы количество единиц было четным. Поэтому, если код переданной строки получен с единственной ошибкой, то количество единиц будет нечетным, и получатель информации поймет, что произошла ошибка.

Коды К сожалению, если произошло две ошибки, их нельзя будет обнаружить, поскольку количество единиц опять будет четным.

Коды Рассмотрим код, в котором для кодирования используется простое повторение кодируемой строки заданное число раз. Например, если при кодировании каждую строку кода нужно повторить один раз, то будет закодировано как . Если при кодировании каждую строку кода нужно повторить дважды, то будет закодировано как .

Коды Если при кодировании каждая строка повторена один раз, то в результате получаем код с обнаружением ошибок. Если произошла ошибка, то соответствующие позиции не будут совпадать.

Коды Например, если закодированная строка имеет вид 111111010110111011, то ошибки имеются в третьем и в последнем битах. Исправить ошибки мы не можем, поскольку не знаем, в какой из копий какая ошибка присутствует. Если кодируемая строка повторяется дважды, то лучше всего выявить ошибку. Если имеются три копии строки, то можно исправить код при наличии единственной ошибки.

Коды Если имеется отличие в битах в соответствующих позициях строк, то выбирается значение, которое встречается дважды. Например, если строка имеет длину 4 и нам передано 110110011101, то во второй позиции мы два раза получим 1 и один раз 0. Таким образом, предполагаем, что правильное значение равно 1, и правильным вариантом закодированной строки является 1101.

Коды Конечно, если ошибка появляется в одной и той же позиции строки более одного раза, возникает проблема. Если строка повторена так, что имеется ее копий, то исправление ошибки дает правильный результат, если при повторении ошибка встречается в одной и той же позиции менее, чем раз.

Порождающие матрицы С этого момента мы будем предполагать, что все строки кода имеют фиксированную длину , и будем трактовать эти строки как векторы или -матрицы. Следовательно, можно использовать сложение векторов. Определим сложение по модулю , так что Таким образом,

Порождающие матрицы Если – множество всех двоичных строк длины , то код – подмножество множества .

Напоминание Группа представляет собой множество вместе с бинарной операцией (или произведением) на , обладающей следующими свойствами: для всех и из (т.е. операция на ассоциативна). В существует элемент , называемый единицей, который обладает свойством: для всех из Для каждого элемента из множества существует элемент из множества , который называется обратным элементом для и такой, что

Напоминание Подмножество группы является подгруппой группы , если с той же самой операцией, что и , также является группой.

Порождающие матрицы Если – множество всех двоичных строк длины , то код – подмножество множества . Множество вместе с указанной выше операцией сложения образует группу относительно сложения. Каждая строка из совпадает со своим обратным элементом, так что в этом смысле сложение и вычитание – это одно и то же.

Порождающие матрицы Код называется линейным, если – подгруппа группы . В действительности – линейное векторное пространство. Однако, рассматривая код , мы будем использовать здесь только те свойства, что является группой и что элемент из – вектор, поэтому может быть умножен на матрицу соответствующего размера.

Порождающие матрицы Будет использован также закон дистрибутивности для матриц, согласно которому для любых матриц и , произведение которых определено.

Порождающие матрицы Весом строки кода, обозначаемым , называется количество единиц в строке. Например, если , то .

Порождающие матрицы Предположим, что имеется такая -матрица , что ее первые к столбцов и строк образуют единичную матрицу размера , все столбцы которой различны. Таким образом, матрица имеет вид . Например, является такой матрицей.

Порождающие матрицы Матрица называется порождающей матрицей. Рассмотрим строки порождающей матрицы как векторы или строки кода. Обозначим это множество строк . Например, для матрицы

Порождающие матрицы Пусть – код, образованный всеми векторами, которые являются конечными суммами строк из . – подгруппа . В нашем примере Строку получаем, складывая первые две строки из , поэтому будет принадлежать . Говорят, что группа порождена множеством .

Порождающие матрицы Говорят, что группа порождена множеством . Это является также минимальным множеством, порождающим код , поскольку никакие элементы из не являются суммами других элементов из . То, что группа порождена множеством , обозначим . Код вида (т.е. порожденный строками матрицы ) называется -кодом.

Порождающие матрицы Теорема 1 -код содержит строк. Доказательство. Первые битов строки из определяют элементы . Позиции, в которых находятся единицы в первых битах строки из , показывают, какие строки из были просуммированы. Например, если единицы находятся в первом и третьем битах строки из , то эта строка получена в результате сложения первой и третьей строк кода .

Порождающие матрицы Теорема 1 -код содержит строк. Доказательство. Первые битов строки из определяют элементы . Позиции, в которых находятся единицы в первых битах строки из , показывают, какие строки из были просуммированы. Поскольку существует различных способов сформировать первые к битов, то в коде имеется строк.

Порождающие матрицы Если необходимо передать строки сообщения длины , то мы кодируем их, умножая справа на матрицу . Таким образом, если или , то мы кодируем это сообщение строкой .

Порождающие матрицы В нашем примере закодируем или , как или . Заметим, что строка сообщения совпадает с первыми тремя битами закодированной строки.

Порождающие матрицы В общем случае строка сообщения длины будет совпадать с первыми битами закодированной строки, поскольку единичная матрица , образующая первые столбцов матрицы , просто повторяет исходную строку. Поэтому мы можем осуществлять декодирование, взяв первые битов закодированной строки.

Порождающие матрицы Заметим также, что выше, при умножении на , мы получили Таким образом, закодированная строка является суммой векторов из множества и, следовательно, принадлежит , поскольку – группа.

Порождающие матрицы В общем случае, если – множество строк порождающей матрицы и – код сообщения, то закодированная строка имеет вид Она представляет собой сумму строк из , так как каждое равно либо , либо и, следовательно, принадлежит , поскольку – группа, порожденная множеством .

Порождающие матрицы Отметим, что имеет вид и что передает сообщение. А что делает ? Рассмотрим снова пример лекции: .

Порождающие матрицы Если – строка сообщения, то закодированная строка имеет вид

Порождающие матрицы Таким образом, четвертый бит закодированной строки должен быть равен , пятый бит должен быть равен и шестой бит должен быть равен . Следовательно, если закодированная строка имеет вид , то

Порождающие матрицы Если закодированная строка имеет вид , то Если любая закодированная строка после передачи не удовлетворяет этим соотношениям, то понятно, что при передаче произошла ошибка.

Порождающие матрицы Если закодированная строка имеет вид , то Например, если получена закодированная строка , то, учитывая, что , и , должны иметь, что , Поскольку соотношение для не выполняется, то становится понятным, что имеется ошибка.

Порождающие матрицы Таким образом, матрица служит для контроля точности передачи данных так же, как ранее это делал бит контроля четности.

Порождающие матрицы В общем случае, если имеется закодированная строка и то для имеем

Порождающие матрицы для Закодированная строка должна удовлетворять всем этим соотношениям.

Коды Следующая проблема – исправление ошибки, если известно, что произошла единственная ошибка. Изложенный ниже метод известен как использование лидеров смежных классов. Метод будет проиллюстрирован нашим примером, в котором

Теорема Лагранжа Определение 1 Для подгруппы группы и произвольного из для некоторого из называется левым смежным классом подгруппы группы .

Теорема Лагранжа Лемма 1 Для фиксированной подгруппы группы левые смежные классы подгруппы группы образуют разбиение группы .

Лемма 1 Для фиксированной подгруппы группы левые смежные классы подгруппы группы образуют разбиение группы . Доказательство Каждый левый смежный класс непустой, поскольку для левого смежного класса элемент находится в .

Лемма 1 Для фиксированной подгруппы группы левые смежные классы подгруппы группы образуют разбиение группы . Доказательство Предположим, что пересечение и непустое; пусть элемент принадлежит пересечению. Следовательно, для некоторых и из . Умножая обе части уравнения на , получаем , поэтому по определению обратного элемента имеем: ().

Лемма 1 Для фиксированной подгруппы группы левые смежные классы подгруппы группы образуют разбиение группы . Доказательство. () для всех из Аналогично, Значит, Следовательно, левые смежные классы образуют разбиение группы .

Теорема Лагранжа Лемма 2 Если – конечная группа и – подгруппа группы , то все левые смежные классы подгруппы группы содержат одно и то же количество элементов, а именно, количество элементов, которое находится в подгруппе . Доказательство Пусть – левый смежный класс подгруппы из . Определим таким образом: . – взаимно однозначное соответствие, или биекция.

Теорема Лагранжа Теорема (Лагранж). Если – конечная группа и – подгруппа группы , то порядок делит порядок . Доказательство Если – порядок , – количество левых смежных классов в и – порядок , то согласно двум предыдущим леммам .

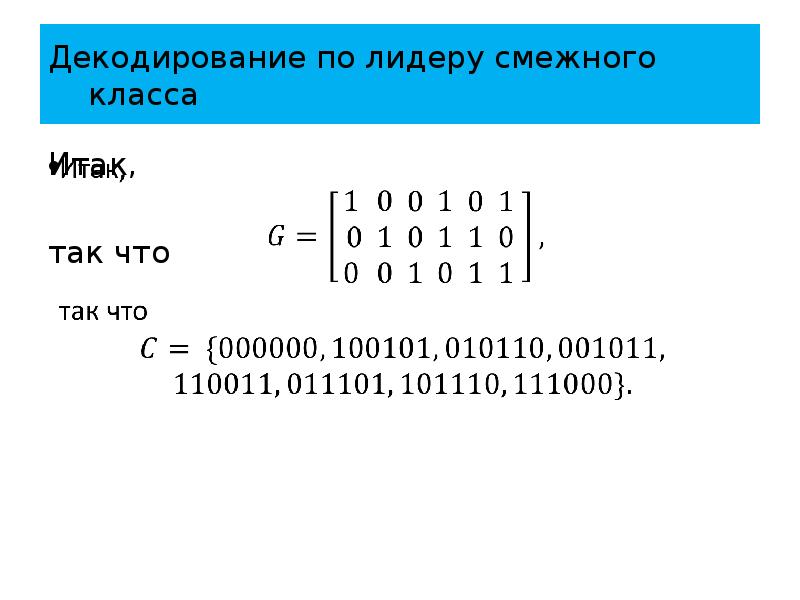
Декодирование по лидеру смежного класса Итак, так что

Декодирование по лидеру смежного класса Сформируем для смежные классы в . Первым смежным классом является сам . Для формирования следующего смежного класса выберем элемент из , который имеет минимальный вес и не принадлежит . Например, можно выбрать . Смежный класс

Декодирование по лидеру смежного класса Опять выбираем элемент из который имеет минимальный вес и не принадлежит ни одному из предыдущих смежных классов. Например, можно выбрать . Смежный класс

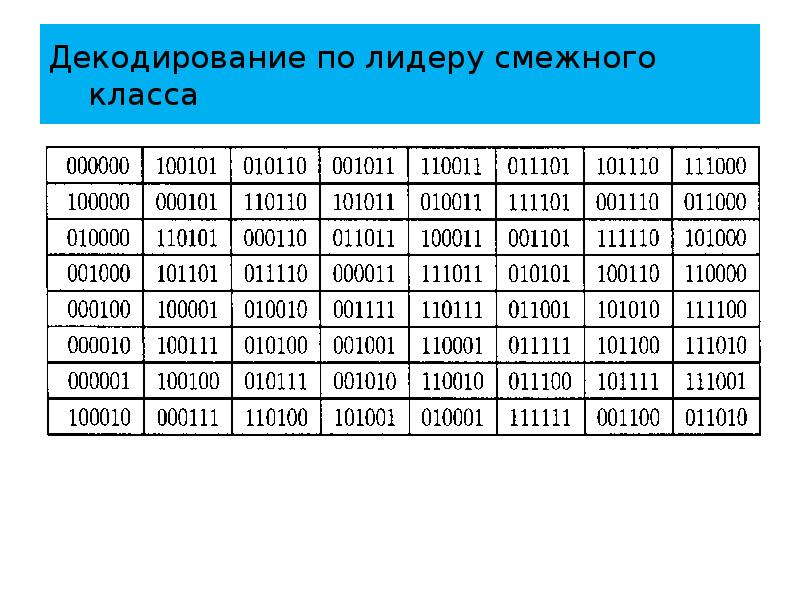
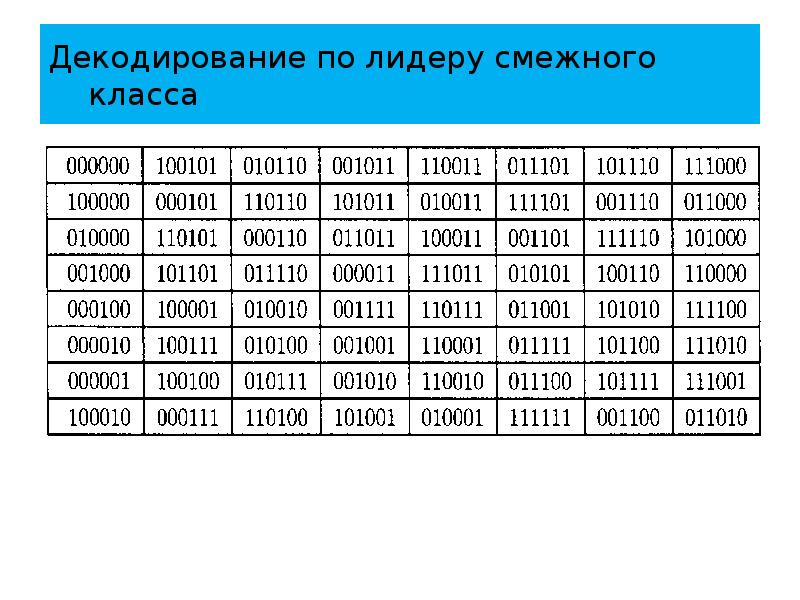
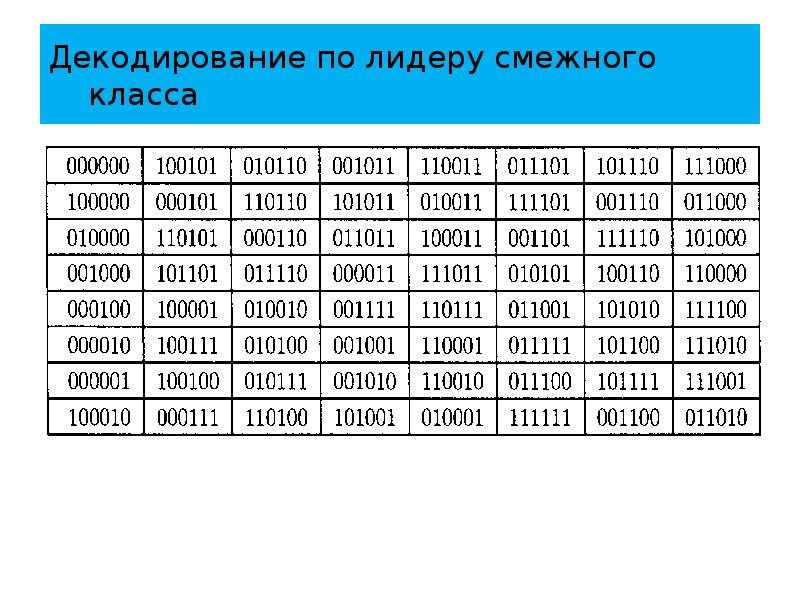
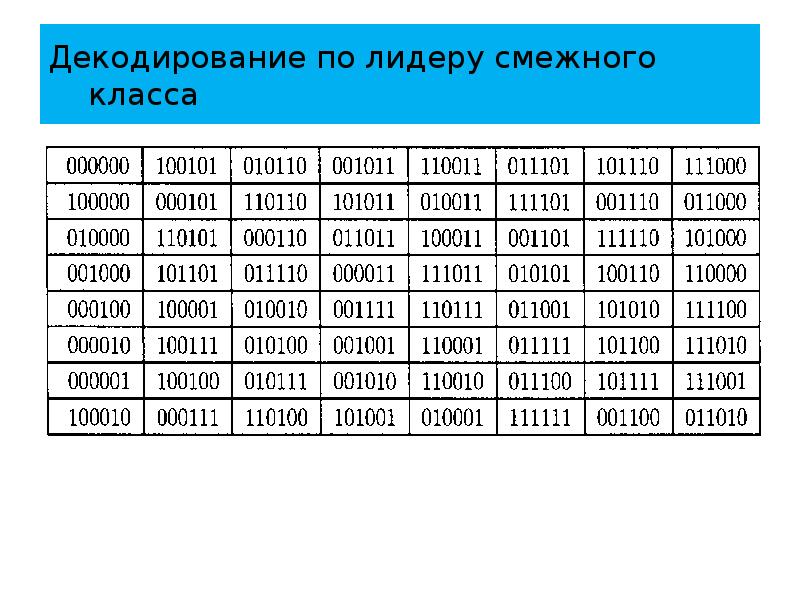
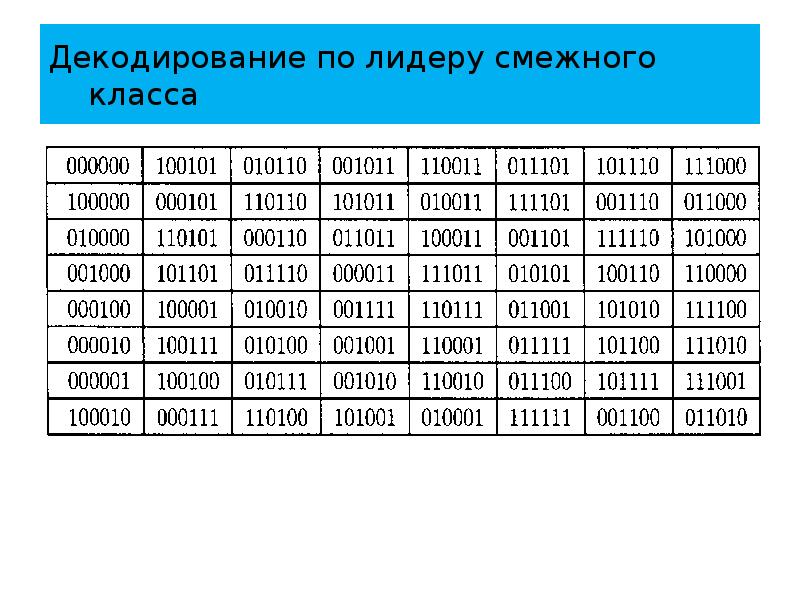
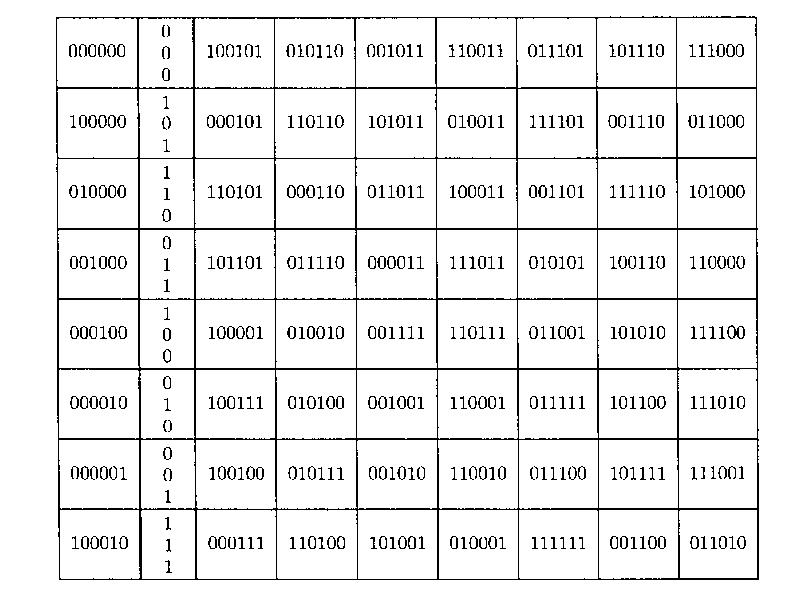
Декодирование по лидеру смежного класса Продолжая этот процесс, получаем следующую таблицу для , разделенного на смежные классы, где элемент минимальным весом выписан первым. Элементы первого столбца называются лидерами смежных классов.

Декодирование по лидеру смежного класса

Декодирование по лидеру смежного класса В последнем смежном классе необходимо использовать строки веса . Можно выбрать одну из строк или .

Декодирование по лидеру смежного класса

Декодирование по лидеру смежного класса Декодирование происходит следующим образом. Получив закодированную строку, ищем ее в таблице. Предположим, например, что получена строка . Смотрим на первый столбец строки, содержащей , и получаем , поэтому предполагаем, что ошибка возникла в первом бите, поскольку была добавлена каждому элементу при построении этого смежного класса. Смотрим на первую строку столбца, содержащего , и получаем , что, по нашему предположению, является правильной строкой кода .

Коды

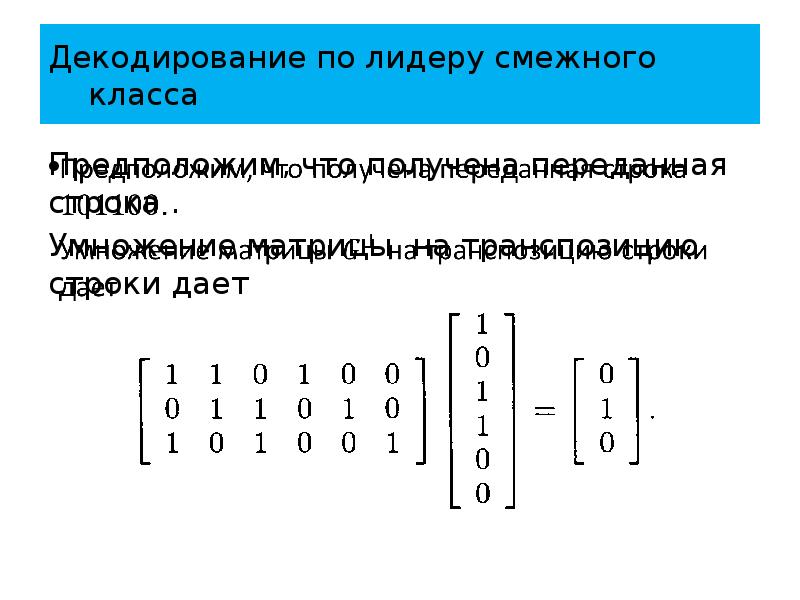
Декодирование по лидеру смежного класса Теперь предположим, что получена строка . Смотрим на первый столбец строки, содержащей , и получаем , поэтому предполагаем, что ошибка возникла в шестом бите. Смотрим на первую строку столбца, содержащего , и находим , что, по нашему предположению, является правильной строкой кода .

Декодирование по лидеру смежного класса

Декодирование по лидеру смежного класса Теперь поищем более простой способ обнаружения ошибок. Пусть и – векторы (или строки) длины . Вектор называется ортогональным вектору , если их скалярное произведение . Пусть задан код . Двойственным кодом к коду , обозначаемым , называется множество всех строк из , ортогональных каждой строке из кода .

Декодирование по лидеру смежного класса – подгруппа группы . Если код является -кодом, так что он порожден строками, то порожден строками.

Декодирование по лидеру смежного класса Пусть – групповой код, а – двойственный ему код. Теорема 2 Строка принадлежит коду тогда и только тогда, когда она ортогональна каждой строке из , множества порождающих элементов кода .

Теорема 2 Строка принадлежит коду тогда и только тогда, когда она ортогональна каждой строке из , множества порождающих элементов кода . Доказательство Если строка принадлежит коду , то она ортогональна каждой строке из множества , поскольку она ортогональна каждой строке из кода и .

Теорема 2 Строка принадлежит коду тогда и только тогда, когда она ортогональна каждой строке из , множества порождающих элементов кода . Доказательство Предположим, что и строка ортогональна строке для всех , так что для всех . Каждый элемент из имеет вид где каждое равно или .

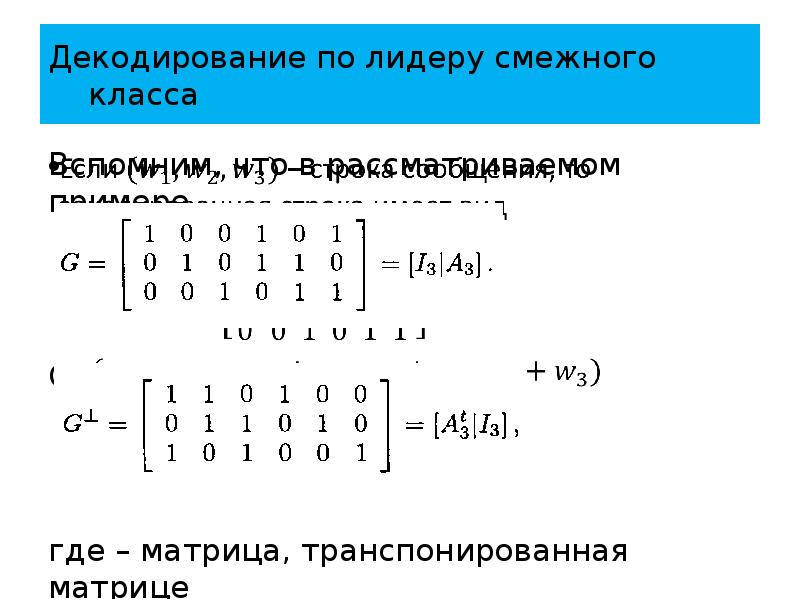
Декодирование по лидеру смежного класса Вспомним, что в рассматриваемом примере Определим теперь где – матрица, транспонированная матрице

Декодирование по лидеру смежного класса Матрица называется матрицей контроля четности.

Декодирование по лидеру смежного класса Перебирая все возможные варианты, можно показать, что скалярное произведение любой строки из с любой строкой из равно . Отсюда получаем, что где — транспозиция -ой строки матрицы . По определению транспозиции является -ой строкой матрицы , преобразованной в столбец. Мы превращаем строку в столбец, чтобы на него можно было умножить матрицу .

Декодирование по лидеру смежного класса Таким образом, если умножить матрицу на транспозицию любого элемента из то получим .

В общем случае, если В общем случае, если то

Декодирование по лидеру смежного класса Скалярное произведение -ой строки матрицы на -ю строку матрицы равно так что в общем случае где – транспозиция -ой строки матрицы Если умножить матрицу на транспозицию любого элемента из , то используя те же рассуждения, мы получим в результате .

Декодирование по лидеру смежного класса Мы также получаем еще один замечательный результат. Если два элемента и из принадлежат одному и тому же смежному классу, образованному в с использованием группы , то

Если два элемента и из принадлежат одному и тому же смежному классу, образованному в с использованием группы , то Доказательство Если и принадлежат одному смежному классу, то для некоторого . Следовательно, и так как для всех .

Декодирование по лидеру смежного класса Поскольку одно и то же для всех из класса смежности, то можно выбрать любое из класса смежности и определить это значение. Таким образом, в каждую строку приведенной выше таблицы можно добавить это общее значение образа , так как элементы каждой строки определяют класс смежности. Мы выбираем лидера смежного класса, потому что он простейший, и помещаем значение его образа во второй столбец. Эти значения называются синдромами.

Декодирование по лидеру смежного класса

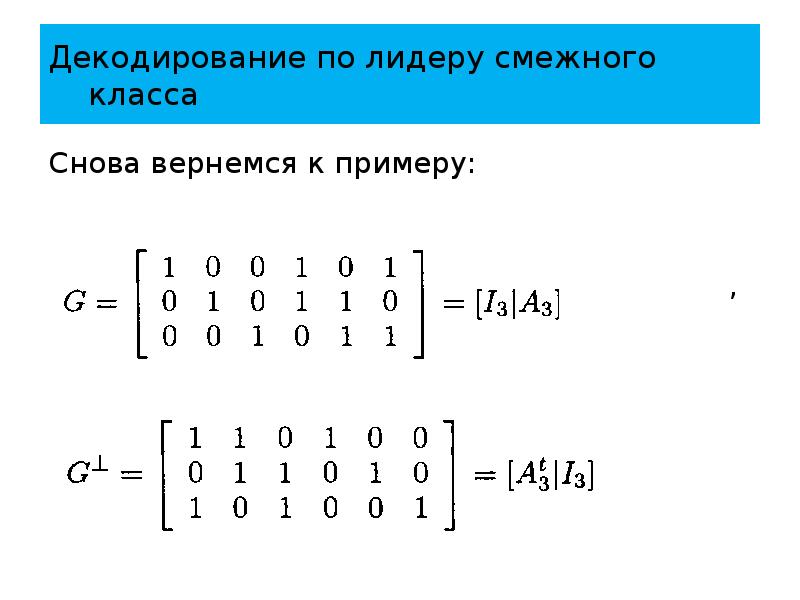
Декодирование по лидеру смежного класса Снова вернемся к примеру: , .

Декодирование по лидеру смежного класса Уже известно, что первый синдром есть .

Декодирование по лидеру смежного класса

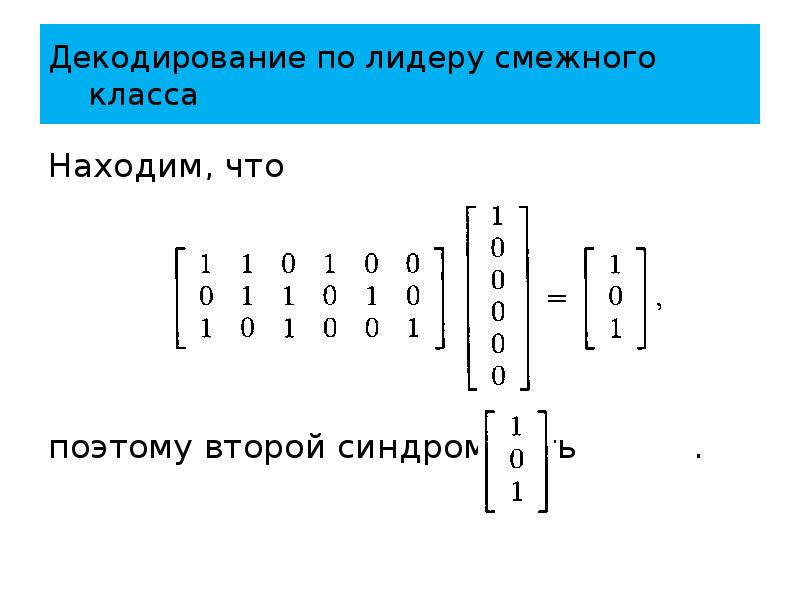
Декодирование по лидеру смежного класса Находим, что поэтому второй синдром есть .

Декодирование по лидеру смежного класса

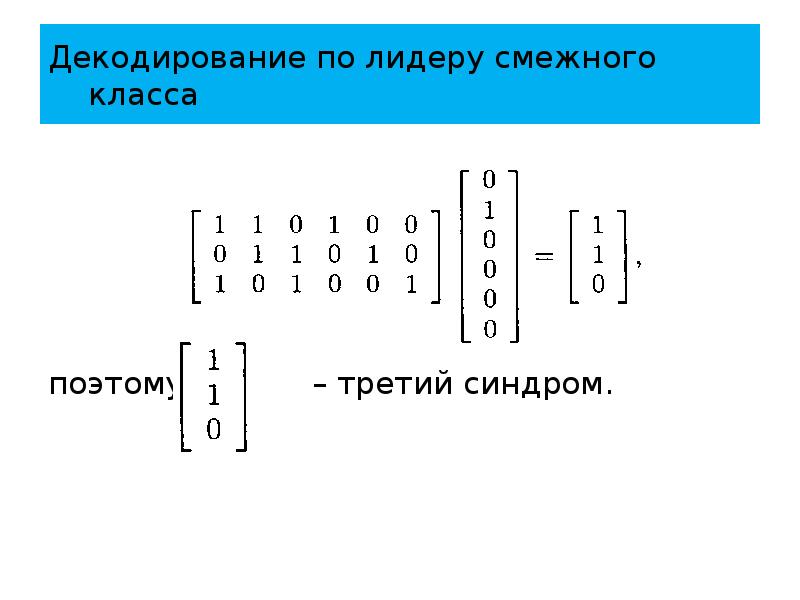
Декодирование по лидеру смежного класса поэтому – третий синдром.

Декодирование по лидеру смежного класса

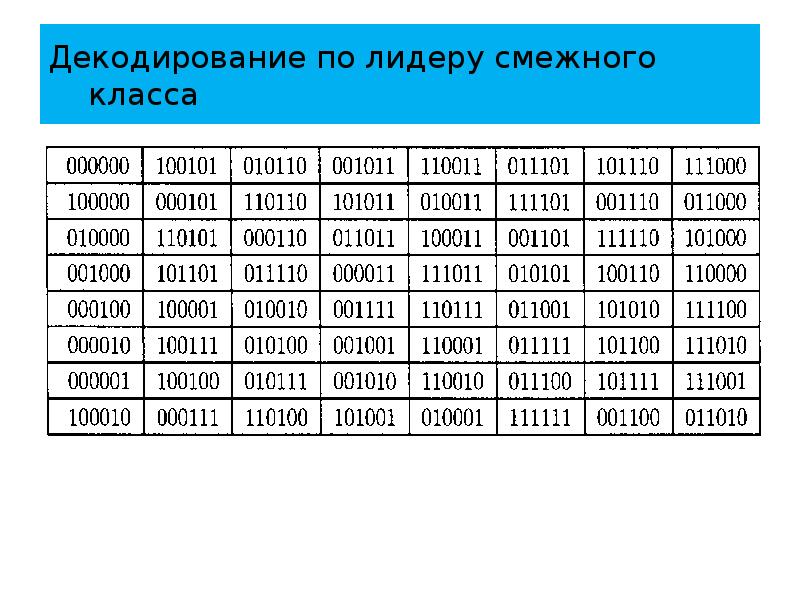
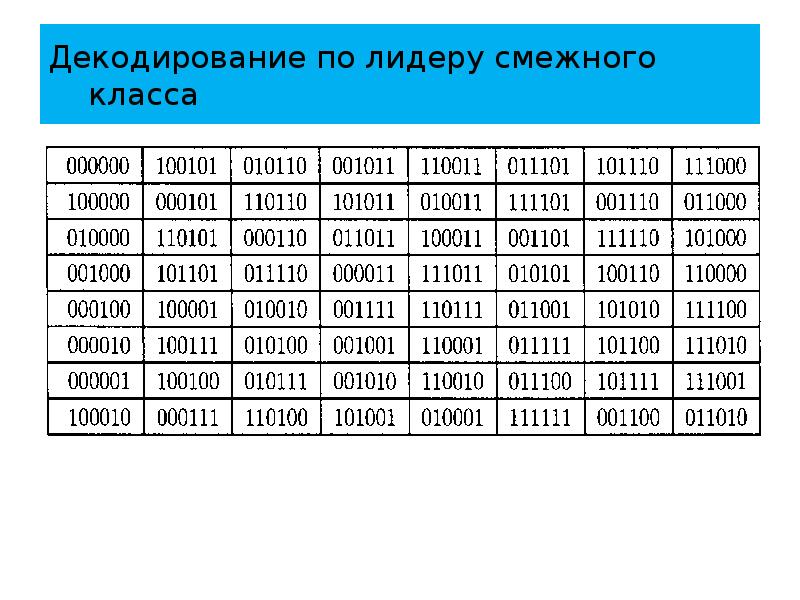
Декодирование по лидеру смежного класса Продолжая процесс, получаем следующую таблицу.

Декодирование по лидеру смежного класса Предположим, что получена переданная строка . Умножение матрицы на транспозицию строки дает

Декодирование по лидеру смежного класса Отсюда следует, что находится в строке . Лидер смежного класса – , элемент крайнего левого столбца строки, содержащей . Элемент кода , расположенный в верхней строке столбца, содержащего , равен . Согласно способу построения таблицы имеем , поэтому можем предположить, что переданная строка должна иметь вид , и в пятом бите была ошибка.

Декодирование по лидеру смежного класса Этот метод намного быстрее, поскольку требует только умножить матрицу на транспозицию строки-сообщения, найти строку, содержащую синдром, и найти переданное сообщение. Лидер для этого сообщения – индикатор ошибки, а элемент кода , расположенный в первой строке столбца, содержащего переданное сообщение, есть исправленное сообщение.

Декодирование по лидеру смежного класса Заметим, однако, что процесс можно сделать еще быстрее. При этом потребуются только два первых столбца приведенной выше таблицы.

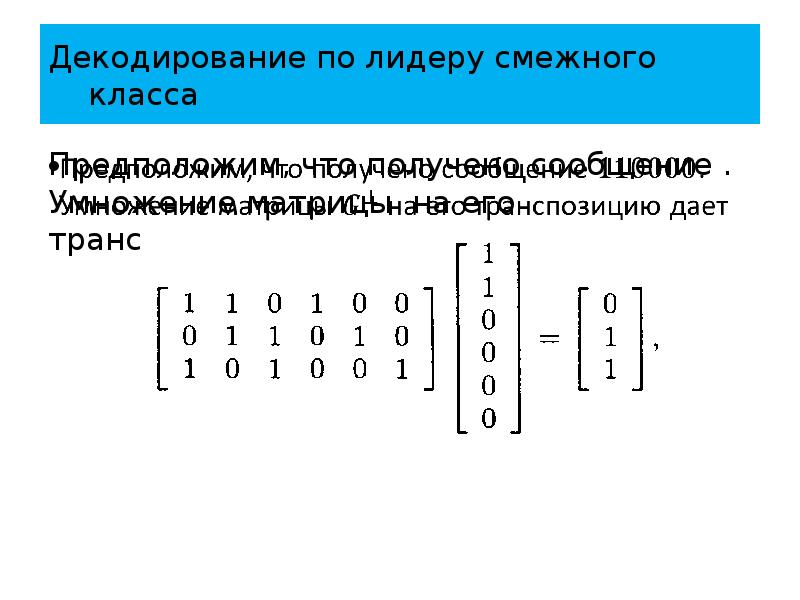
Декодирование по лидеру смежного класса Предположим, что получено сообщение . Умножение матрицы на его транспозицию дает

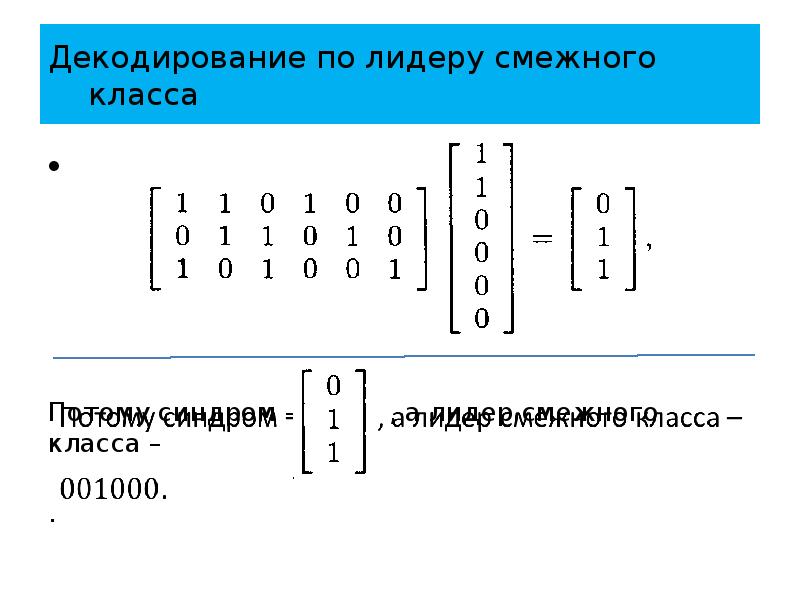
Декодирование по лидеру смежного класса Потому синдром – , а лидер смежного класса – .

Декодирование по лидеру смежного класса Синдром – , лидер смежного класса – . Поскольку лидер указывает, что ошибка появилась в третьем бите, то, добавляя к получаем – исправленный код.

Декодирование по лидеру смежного класса Таким образом, этот метод прост. Умножить транспозицию сообщения на матрицу , чтобы найти синдром. Далее, нужно найти лидера смежного класса и прибавить его к сообщению, чтобы получить исправленный код. Обратите внимание на то, что используются только первые два столбца таблицы!

Декодирование по лидеру смежного класса Однако, теперь возникла еще одна проблема. Если полученным сообщением будет строка , то синдром будет и в соответствующей строке будет три элемента с весом .

Декодирование по лидеру смежного класса Вспомним, что строка была выбрана произвольно. Любая из таких строк равновероятно может содержать ошибку, поэтому в данном случае совершенно безнадежно использовать синдромы для исправления ошибки. Кроме того, мы пытаемся в данном случае исправить строку с двумя ошибками вместо одной.

Коды Хемминга В рассматриваемом примере существуют определенные трудности при попытке исправить код для некоторых строк, поскольку все лидеры имеют вес 1. Эти трудности устраняются путем использования матрицы, называемой матрицей Хемминга, в качестве порождающей матрицы.

Коды Хемминга Перед тем как перейти к рассмотрению матрицы Хемминга , посмотрим на матрицу контроля четности . Пусть – матрица, в которой таких строк, что столбцы состоят из всевозможных строк длины , за исключением строки, состоящей только из нулей. Предположим, что . Существует таких строк, поэтому есть матрица, где .

Коды Хемминга Будем использовать столбцы с весом как последние столбцов, формирующих единичную матрицу, так что матрица имеет вид , где – -матрица. Матрица Хемминга – это -матрица вида , – -матрица. Код, образованный строками матрицы Хемминга, называется кодом Хемминга.

Коды Хемминга Например, пусть и – матрица Тогда – матрица

Коды Хемминга Для изучения матриц Хемминга необходимо понятие расстояния и его связь с весом каждой из строк. Начнем с теоремы о весах строк.

Коды Хемминга Теорема 3 Для строк и вес Доказательство Пусть и . Если , то либо , либо . Поэтому существованию каждой единицы в соответствует существование единицы либо в , либо в .

Коды Хемминга Расстояние Хемминга, или просто расстояние между двумя строками кода и , имеющими одинаковую длину, это число соответствующих битов в строке, где одна строка имеет цифру 1, а другая имеет цифру 0. Будем обозначать функцию расстояния через .

Коды Хемминга Например, если и , то , так как две строки отличаются во второй, третьей и шестой позициях. Очевидно, что чем больше расстояние между двумя строками кода, тем больше ошибок можно обнаружить. Поскольку названа функцией расстояния, мы должны показать, что она обладает основными свойствами функции расстояния.

Коды Хемминга Теорема 4 Функция расстояния Хемминга имеет следующие свойства: для строк и расстояние тогда и только тогда, когда ; для строк и расстояние ; для строк , и выполняется соотношение .

Коды Хемминга Доказательство Первые два пункта следуют из определения. Докажем c). Для строк и вес Если и то вносит 1 в вес тогда и только тогда, когда и Но это верно в том и только в том случае, когда и различны, что вносит 1 в .

Коды Хемминга Доказательство Заметим, что для любой строки строка состоит только из нулей. Обозначим такую строку через . для каждой строки . Следовательно,

Коды Хемминга Важно знать минимальное расстояние между двумя строками кода. Если – код, то минимальное расстояние кода , обозначаемое , равно наименьшему расстоянию между двумя строками из .

Коды Хемминга В приведенной далее теореме сформулирован важный критерий для определения числа ошибок, которые могут быть исправлены или обнаружены с использованием кода.

Коды Хемминга Теорема 5 Для кода , если , то использование кода позволяет обнаружить вплоть до ошибок; если , то использование кода позволяет исправить вплоть до ошибок.

Коды Хемминга Доказательство a) Если , то для данной строки отсюда следует, что отличается от любой другой строки кода по крайней мере в позициях. Поэтому, если переданная строка имеет или менее ошибок, то она не может быть другой строкой кода, и ошибка определена.

Коды Хемминга Доказательство b) Если строка передана как с или менее ошибками, то для любой строки имеем . Если для некоторой строки из расстояние , то . Но и что приводит к противоречию. можно исправить на – единственную строку, расстояние которой от меньше, чем

Коды Хемминга Возникает проблема определения , наименьшего расстояния между любыми двумя строками из кода .

Коды Хемминга Теорема 6 Минимальное расстояние кода равно . Доказательство По определению , существуют такие, Обратно, для имеем Следовательно, Отсюда

Коды Хемминга Задание Построить код Хэмминга. Изучить корректирующие способности кода Хэмминга. Показать, что синдромы указывают позиции ошибок.