Теория комплексных чисел. Геометрическая интерпретация комплексного числа. (Тема 3) презентация
Содержание
- 2. Геометрическая интерпретация комплексного числа XVIII-XIX вв Г.Вессель, Ж.Арган, К. Гаусс
- 3. 1. Изобразить на комплексной плоскости следующие числа:
- 4. Модуль комплексного числа Модулем комплексного числа z=a+bi называется длина вектора
- 5. 2. Найти модуль комплексного числа:
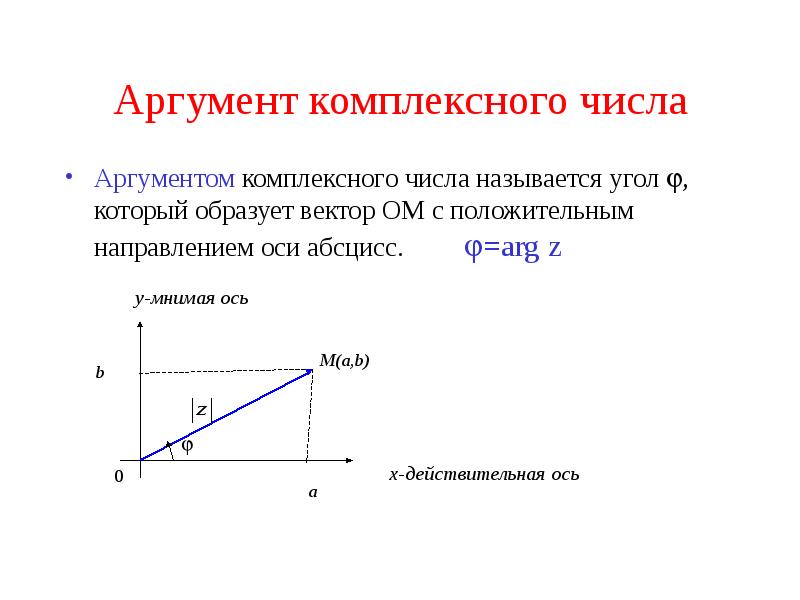
- 6. Аргумент комплексного числа Аргументом комплексного числа называется угол , который образует
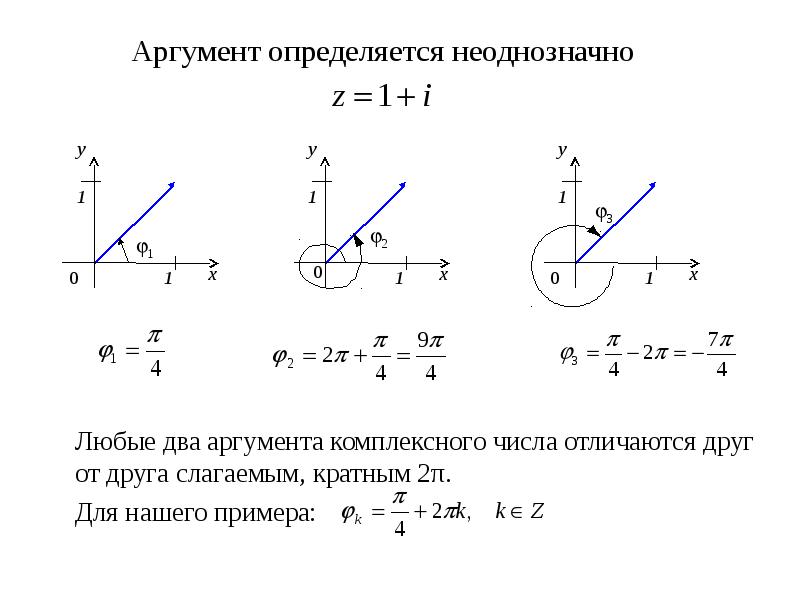
- 7. Аргумент определяется неоднозначно Любые два аргумента комплексного числа отличаются друг от
- 8. 3. Найти аргументы комплексного числа:
- 9. 4.Найти модуль и аргумент комплексного числа:
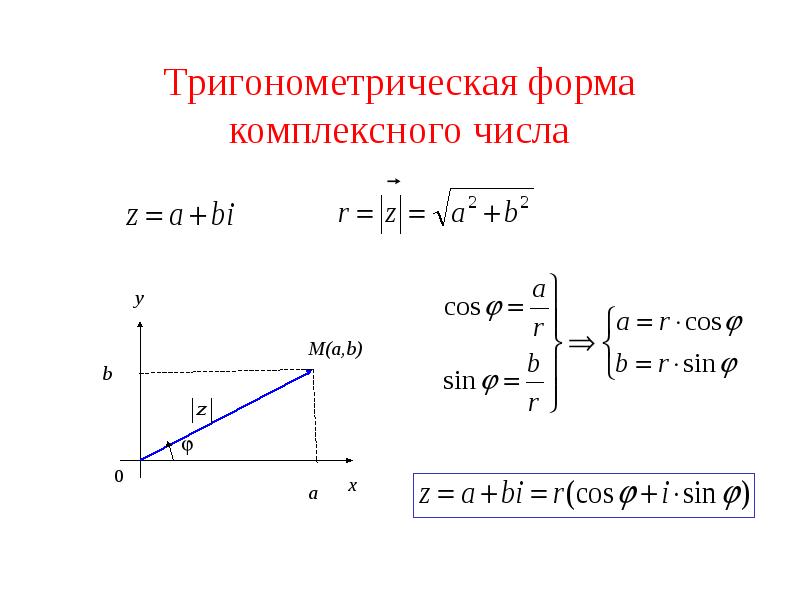
- 10. Тригонометрическая форма комплексного числа
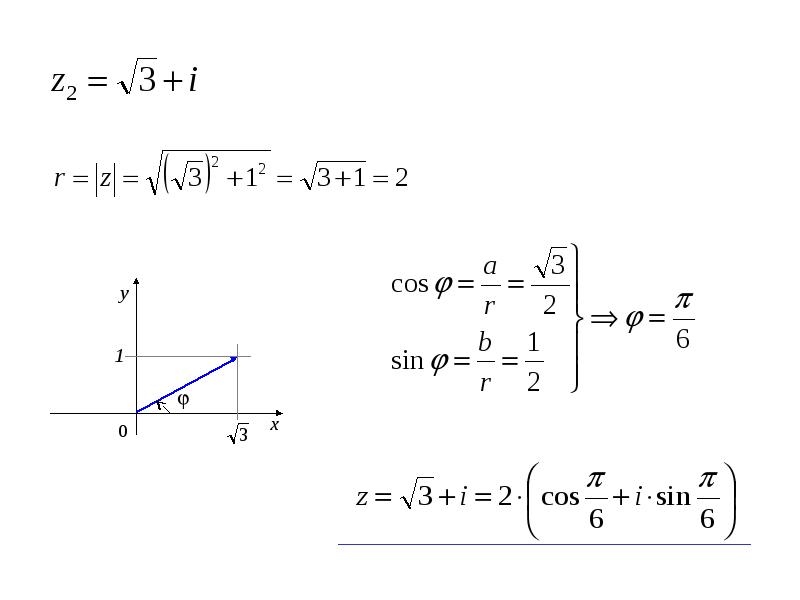
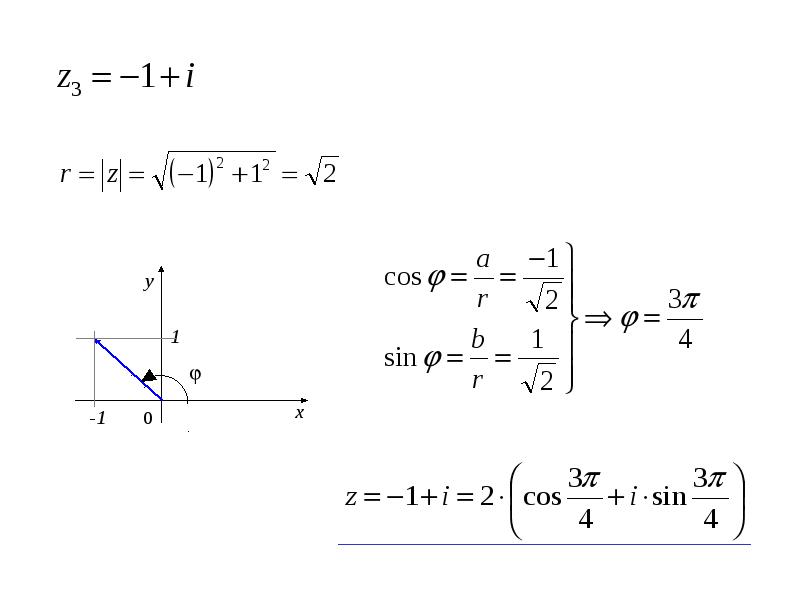
- 11. 5.Записать число в тригонометрической форме:
- 12. 6. Записать число в алгебраической форме:
- 13. 7. Записать число в алгебраической форме:
- 14. Действия над комплексными числами в тригонометрической форме Умножение комплексных чисел. Пусть
- 15. 8. Найти произведение комплексных чисел:
- 17. 9. Найти частное комплексных чисел:
- 18. 10. Записать в тригонометрической форме комплексное число:
- 19. Пусть Пусть
- 23. Действия над комплексными числами в тригонометрической форме. Возведение в степень. Пусть
- 24. 12. Возвести в степень комплексное число и записать результат в алгебраической
- 26. Разделим одно число на другое в тригонометрической форме:
- 27. Теперь можно результат записать в алгебраической форме:
- 28. Действия над комплексными числами в тригонометрической форме. Извлечение корня. Пусть
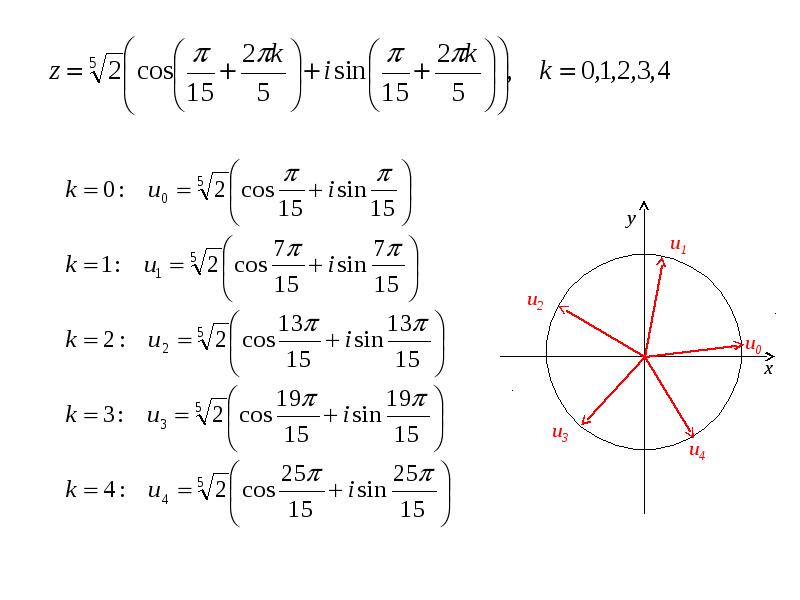
- 29. 13. Найти все значения корня:
- 31. 14. Решить уравнение:
- 34. 15. Сделать действия в тригонометрической форме и ответ записать в алгебраической
- 35. 16. Сделать действия над комплексными числами и ответ записать в тригонометрической
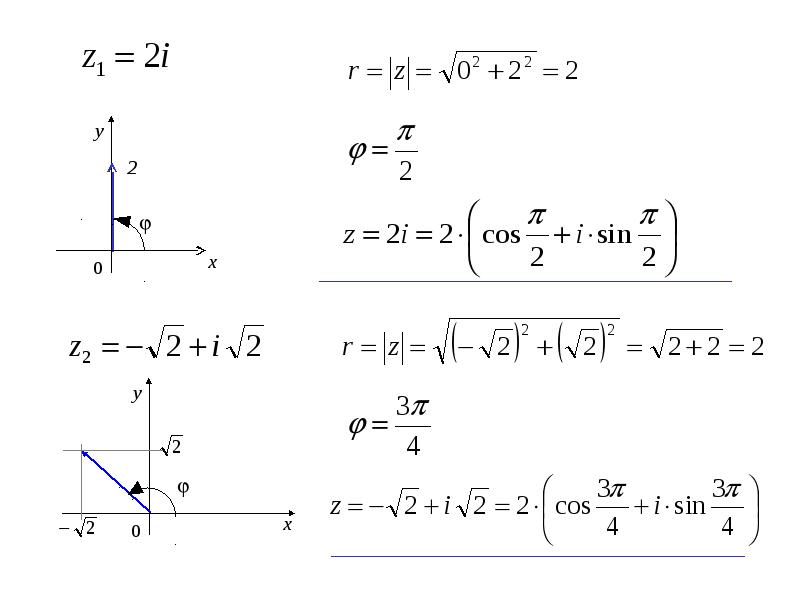
- 36. 17. Представить числа в тригонометрической форме:
- 37. 18. Найти в тригонометрической форме для чисел
- 38. 19. Найти в тригонометрической форме и результат представить в алгебраической форме, если
- 39. 20. Найти все значения корня:
- 40. Скачать презентацию
















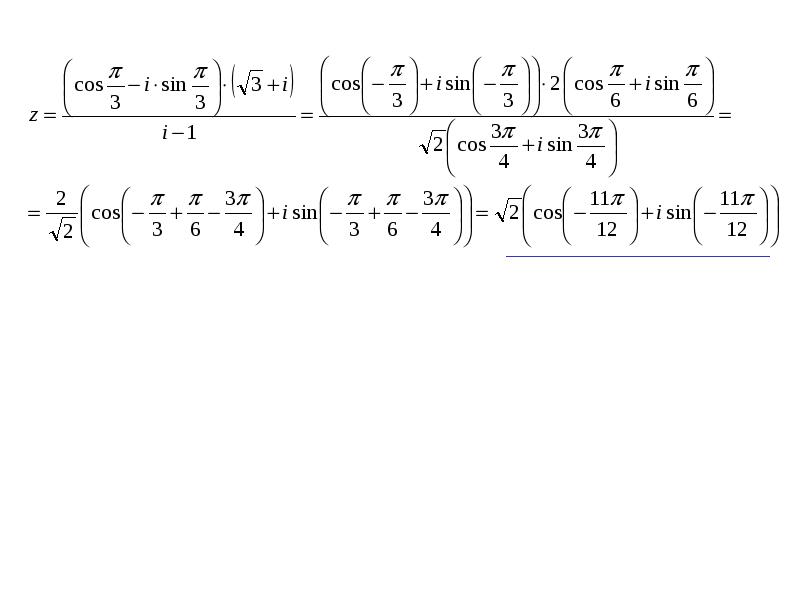















Слайды и текст этой презентации
Скачать презентацию на тему Теория комплексных чисел. Геометрическая интерпретация комплексного числа. (Тема 3) можно ниже:
Похожие презентации





























