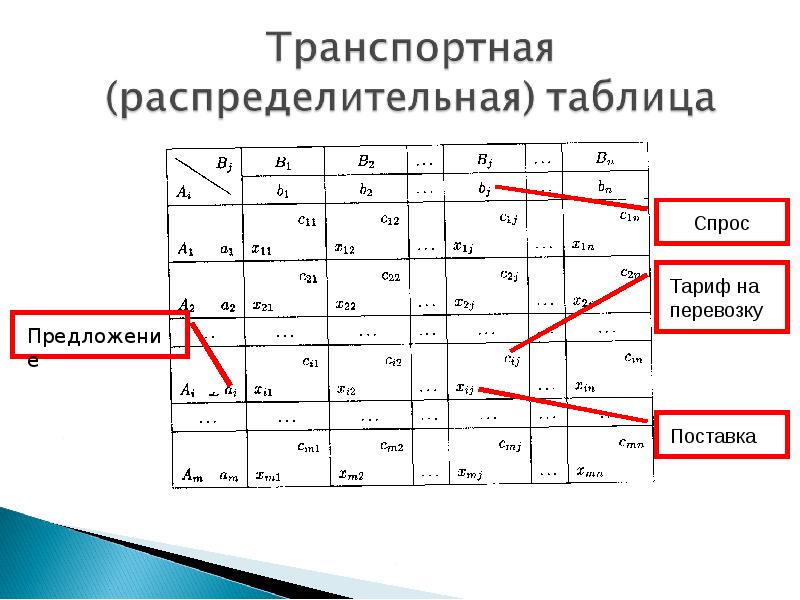
Транспортная задача. Двухиндексные задачи линейного программирования презентация
Содержание
- 2. В пунктах производства A1, A2, ..., Am имеется однородный груз в
- 4. В зависимости от соотношения между суммарными запасами груза и суммарными потребностями
- 5. При ограничениях Оптимальным решением задачи является матрица
- 6. Транспортная задача как задача линейного программирования может быть решена симплексным методом,
- 7. На складах A1, А2, А3 имеются запасы продукции в количествах 90,
- 8. Проверим, является ли задача закрытой: Проверим, является ли задача закрытой:
- 10. Рассмотрим один из методов — метод минимального тарифа: Рассмотрим один из
- 11. При распределении грузов может оказаться, что количество занятых клеток меньше, чем
- 12. Найдем исходное опорное решение методом наименьшего тарифа: Найдем исходное опорное решение
- 13. Найденное исходное опорное решение проверяется на оптимальность методом потенциалов. Найденное исходное
- 14. Обозначим Δij = ui + vj - cij. Обозначим Δij
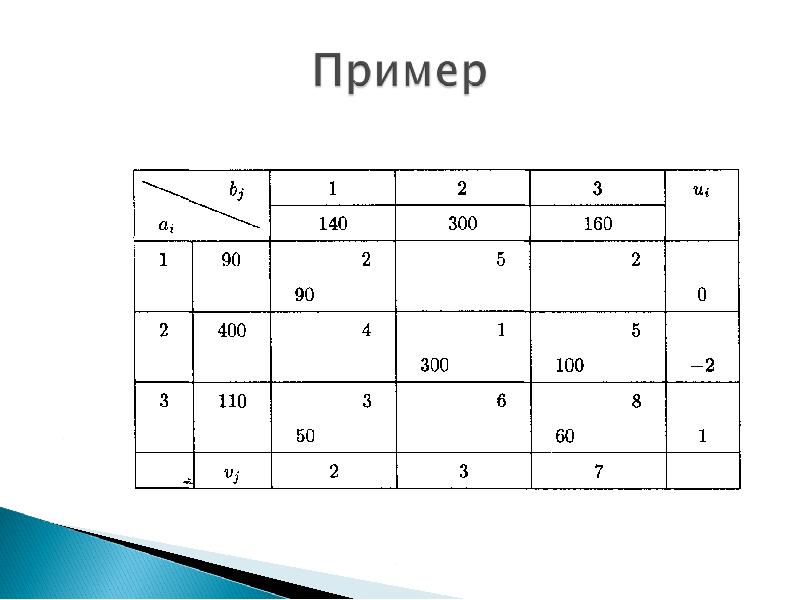
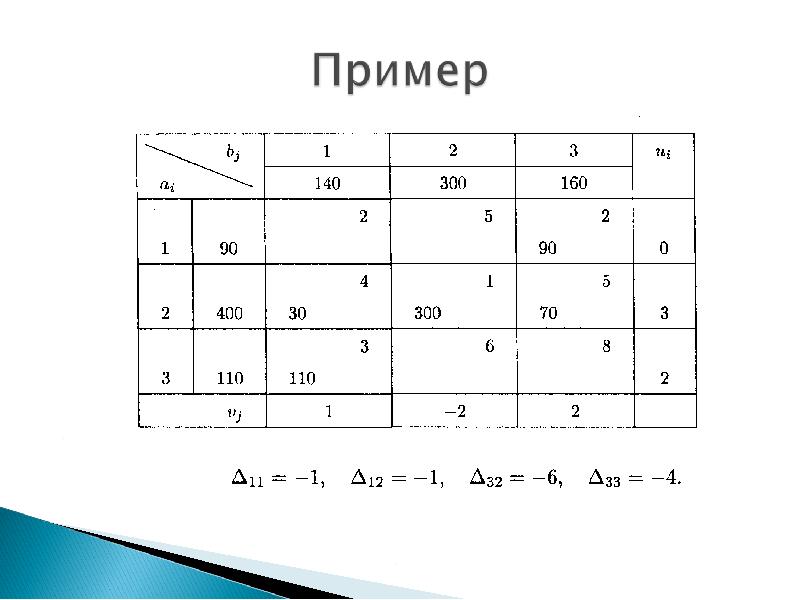
- 15. Проверим найденное опорное решение на оптимальность, добавив в таблицу столбец ui
- 17. Вычисляем оценки свободных клеток: Вычисляем оценки свободных клеток: Получили оценку Δ13
- 18. Переход к другому опорному решению осуществляется перераспределением грузов, перемещая их из
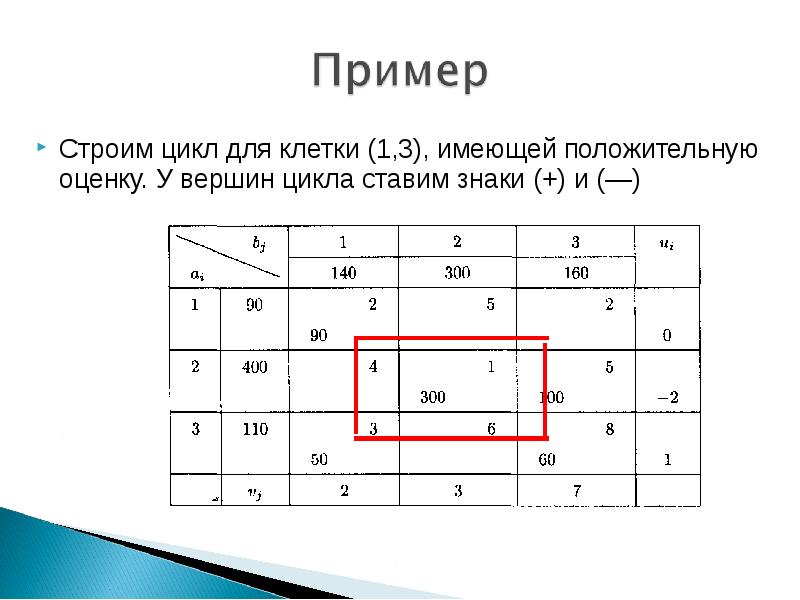
- 19. Строим цикл для клетки (1,3), имеющей положительную оценку. У вершин цикла
- 20. У вершин со знаком (—) выбираем минимальный груз, он равен 60.
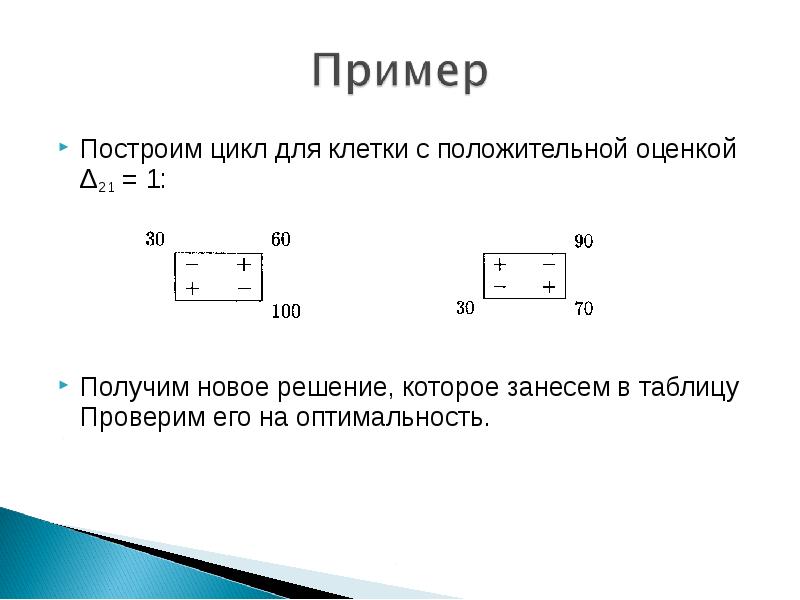
- 22. Построим цикл для клетки с положительной оценкой Δ21 = 1: Построим
- 24. Все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное. Все
- 25. При открытой транспортной задаче сумма запасов не совпадает с суммой потребностей
- 26. При введении фиктивного участника открытая транспортная задача становится закрытой и решается
- 27. Признак наличия альтернативного оптимума в ТЗ: равенство нулю хотя бы одной
- 28. На трех складах имеется мука в количестве 60, 130 и 90
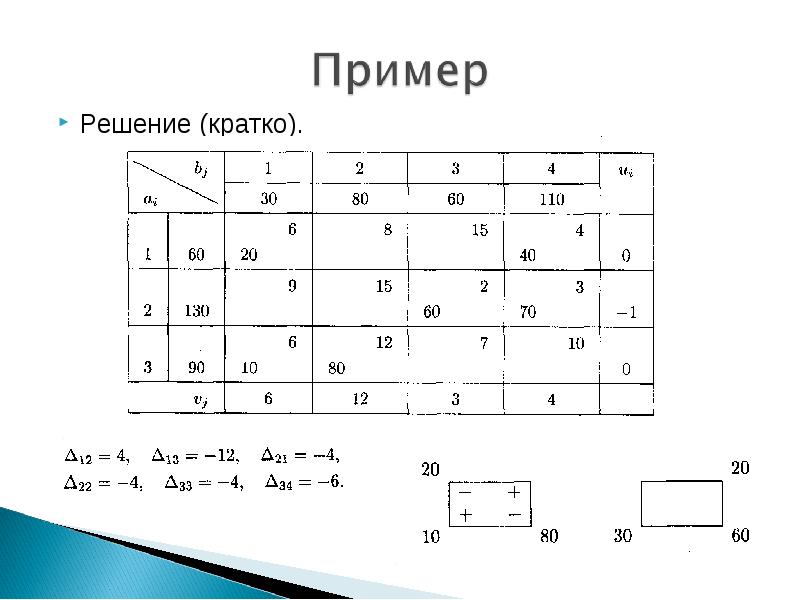
- 29. Решение (кратко). Решение (кратко).
- 30. Решение (кратко). Решение (кратко).
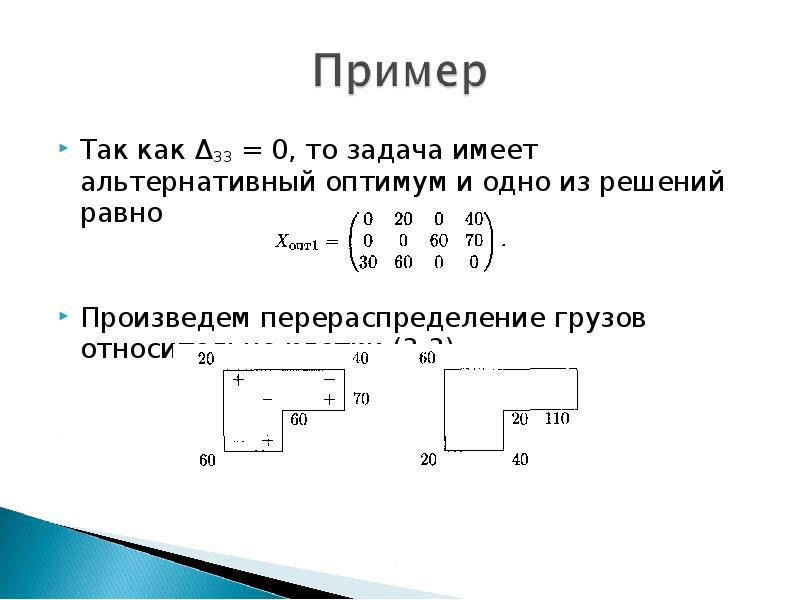
- 31. Так как Δ33 = 0, то задача имеет альтернативный оптимум и
- 32. Теперь Δ14 = 0, получили еще одно решение: Теперь Δ14 =
- 33. Найдем элементы матрицы общего решения: Найдем элементы матрицы общего решения: Итак,
- 34. Скачать презентацию


























Слайды и текст этой презентации
Скачать презентацию на тему Транспортная задача. Двухиндексные задачи линейного программирования можно ниже:
Похожие презентации





























