Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 2 семестр презентация
Содержание
- 2. 6.1. Основные понятия Системой линейных алгебраических уравнений, содержащей m уравнений и
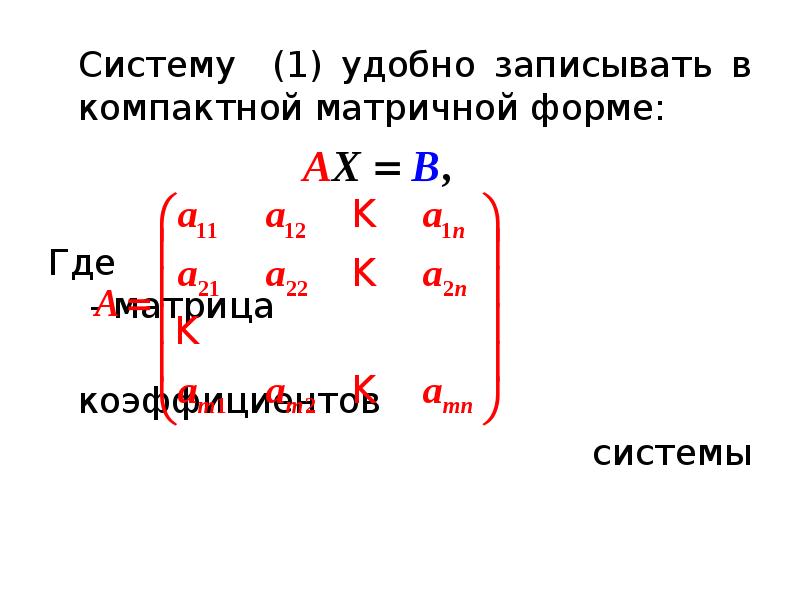
- 3. Систему (1) удобно записывать в компактной матричной форме: Систему (1) удобно
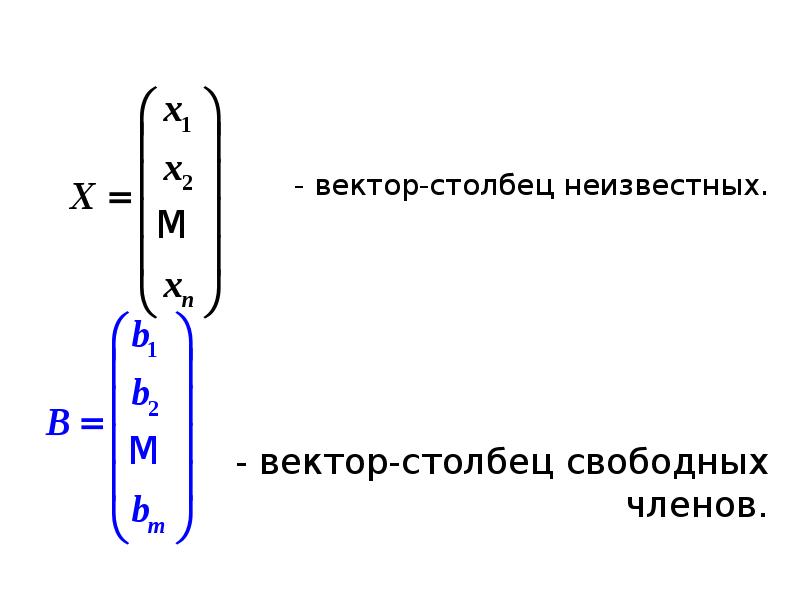
- 4. - вектор-столбец неизвестных. - вектор-столбец неизвестных.
- 5. ОПР. Расширенной матрицей системы (1) называется матрица системы, дополненная столбцом свободных
- 6. Решение системы Упорядоченное множество чисел называется решением системы (1),
- 7. Совместная система уравнений называется определенной, если она имеет единственное решение, и
- 8. Решить систему – это значит выяснить совместна она или несовместна. Если
- 9. Система линейных уравнений называется однородной, если все свободные члены равны нулю:
- 10. 6.2. Решение невырожденных линейных систем. Формулы Крамера Рассмотрим систему n
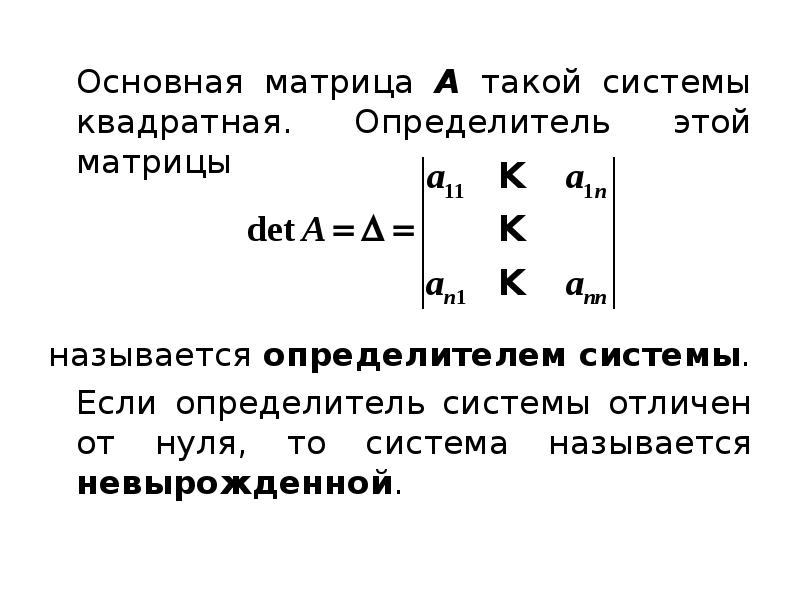
- 11. Основная матрица A такой системы квадратная. Определитель этой матрицы Основная
- 12. Решение системы трех уравнений с тремя неизвестными Система трёх уравнений с
- 13. Определитель системы
- 14. Система (2) может быть представлена в виде Система (2) может
- 15. При и хотя бы одном из При
- 16. Пример Решить систему по формулам Крамера
- 17. Найдем определитель системы Найдем определитель системы
- 18. Вычислим Вычислим
- 19. По формулам Крамера находим Ответ:
- 20. 6.3. Исследование и решение СЛАУ. Теорема Кронекера-Капелли Рассмотрим произвольную СЛАУ (1)
- 21. Теорема 6.2. Если ранг совместной системы равен числу неизвестных, то система
- 22. 6.4. Метод Гаусса Метод Гаусса (или метод последовательного исключения неизвестных) является
- 23. С помощью элементарных преобразований система уравнение приводится к равносильной системе ступенчатого
- 24. Процесс решения по методу Гаусса состоит из двух этапов: Процесс решения
- 25. Элементарные преобразования Перестановка уравнений местами. Умножение какого-либо уравнения системы на число,
- 26. Рассмотрим метод Гаусса для системы третьего порядка, определитель которой не равен
- 27. Исключим из второго и третьего уравнений, используя элементарные преобразования системы а
- 28. После этого начинается обратный ход метода Гаусса: из последнего уравнения находим
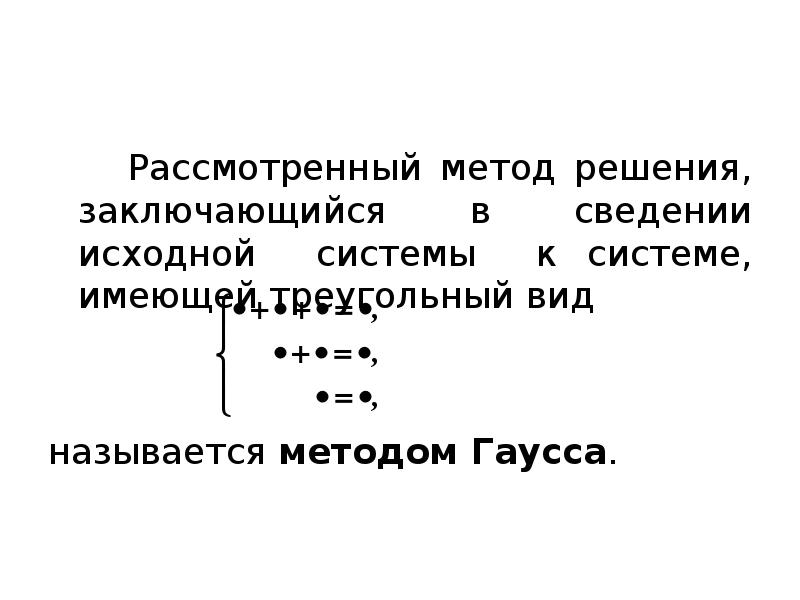
- 29. Рассмотренный метод решения, заключающийся в сведении исходной системы к системе, имеющей
- 30. Пример Рассмотрим систему
- 31. Исключим x из второго и третьего уравнения. Для этого первое уравнение
- 32. Получим систему, равносильную данной: Получим систему, равносильную данной: Далее исключим y
- 33. Из третьего уравнения подставим во второе и найдем
- 34. Пример Решить систему методом Гаусса Решение. Поменяем местами первое и второе
- 35. Получим систему Получим систему Последнее равенство неверно. Следовательно, система несовместна. Ответ:
- 36. Пример Решить систему методом Гаусса Решение. Умножим первое уравнение на (-2)
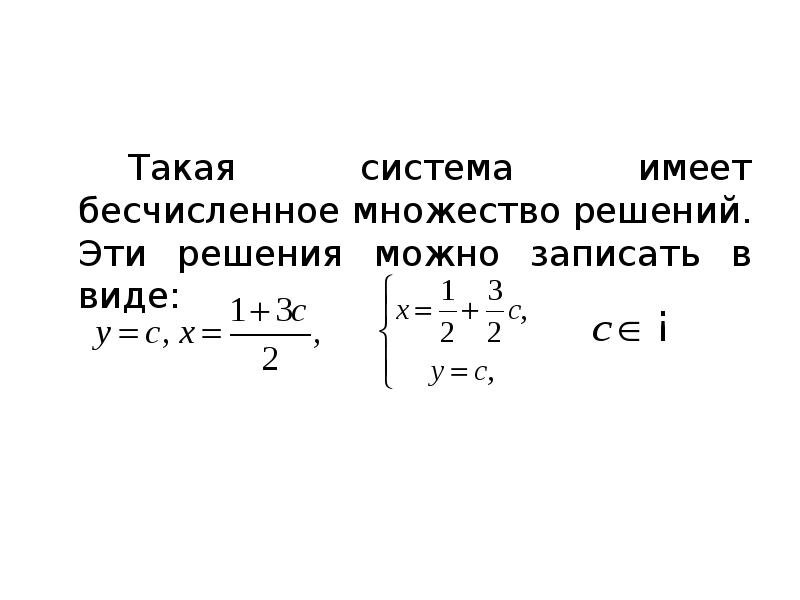
- 37. Такая система имеет бесчисленное множество решений. Эти решения можно записать в
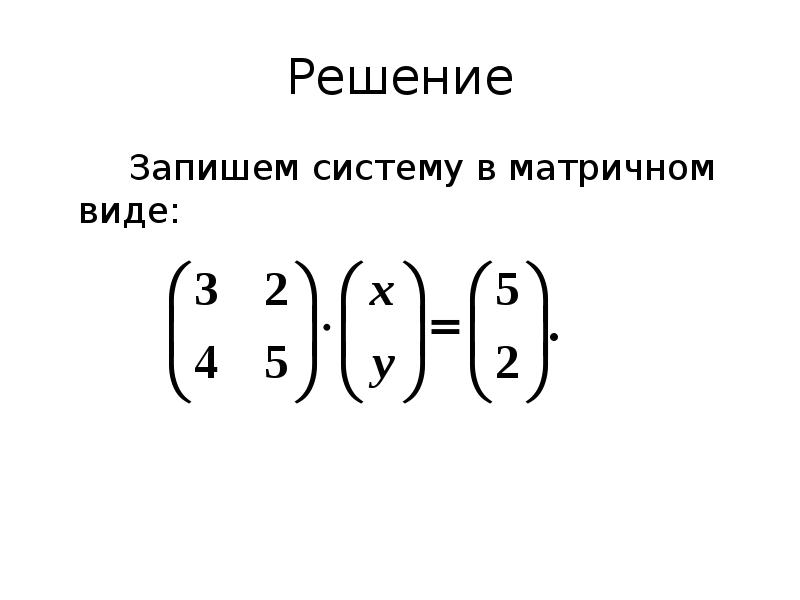
- 38. Пример 1. Установить, совместна ли система и, если она совместна, найти
- 39. Решение Запишем систему в матричном виде:
- 40. Определитель системы равен Определитель системы равен
- 41. Найденное решение - это точка пересечения прямых Найденное
- 42. 2. Установить, совместна ли система и, если она совместна, найти ее
- 43. Определитель системы: Определитель системы: Определитель отличен от нуля, следовательно система
- 44. Так как каждое уравнение системы – это уравнение прямой и система
- 45. Тема: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- 46. Линия на плоскости часто задается как множество точек, обладающих некоторым только
- 47. ОПР. Уравнением линии (или кривой) на плоскости Оху называется такое уравнение
- 48. §1. Уравнения прямой на плоскости Простейшей из линий является прямая.
- 49. 1.1. Различные виды уравнений прямой Уравнение называется общим уравнением
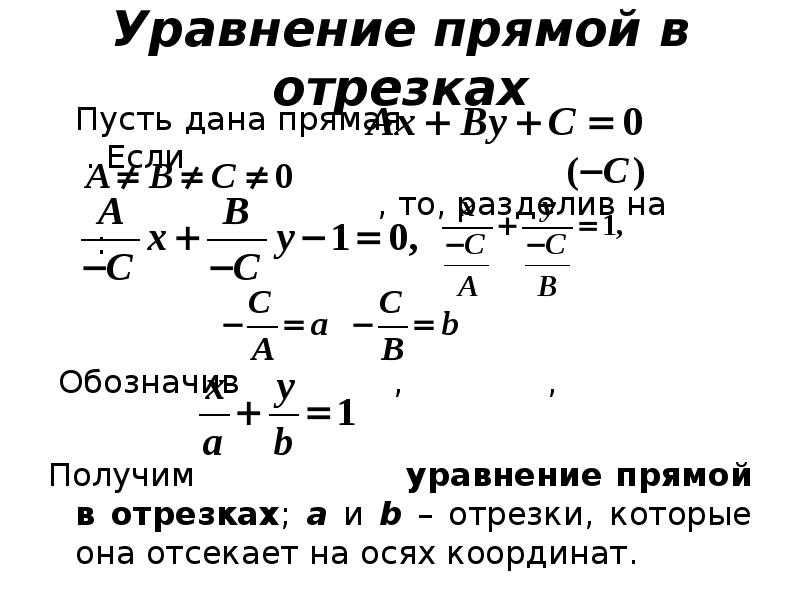
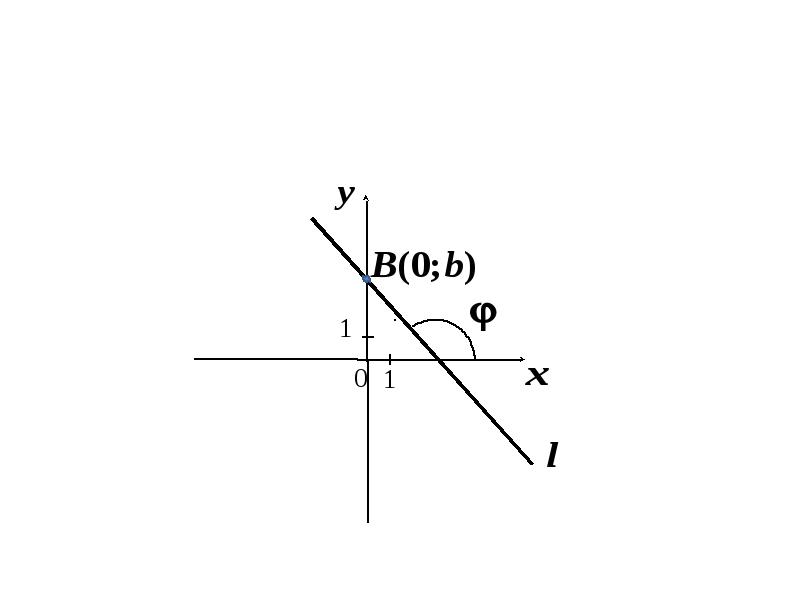
- 50. Уравнение прямой в отрезках Пусть дана прямая
- 51. Пример Записать уравнение прямой в отрезках.
- 52. Уравнение прямой с угловым коэффициентом k Дана прямая , которая
- 54. Пусть – произвольная точка прямой. Пусть
- 55. Уравнение прямой, проходящей через данную точку в данном направлении k Пусть
- 56. Уравнение прямой, проходящей через две данные точки
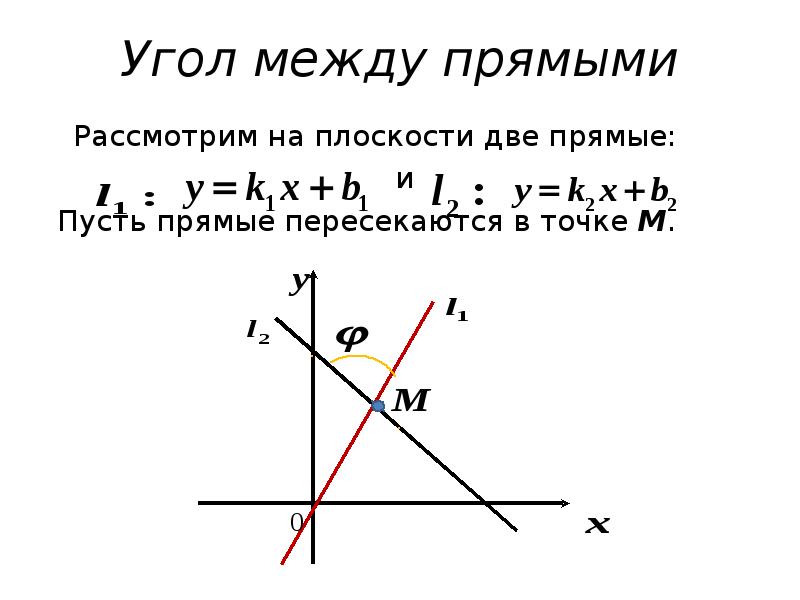
- 57. Угол между прямыми Рассмотрим на плоскости две прямые: и Пусть прямые
- 58. Углом между прямыми и будем называть наименьший угол, на который надо
- 59. Угол между прямыми: Угол между прямыми: Взаимное расположение двух прямых:
- 60. Расстояние от точки до прямой Расстояние d от точки
- 61. Тема: Элементы векторной алгебры
- 62. §1. Векторы 1.1. Основные понятия Величины, которые полностью определяются своим численным
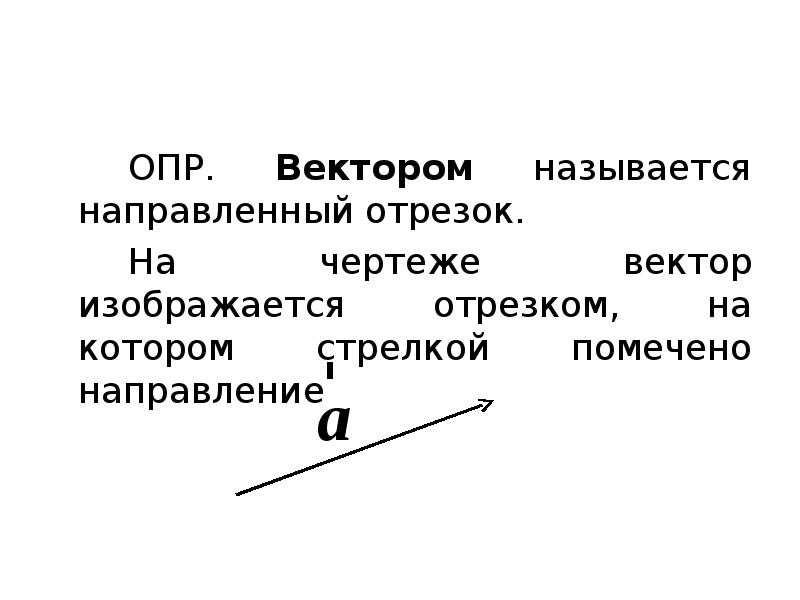
- 63. ОПР. Вектором называется направленный отрезок. На чертеже вектор изображается отрезком, на
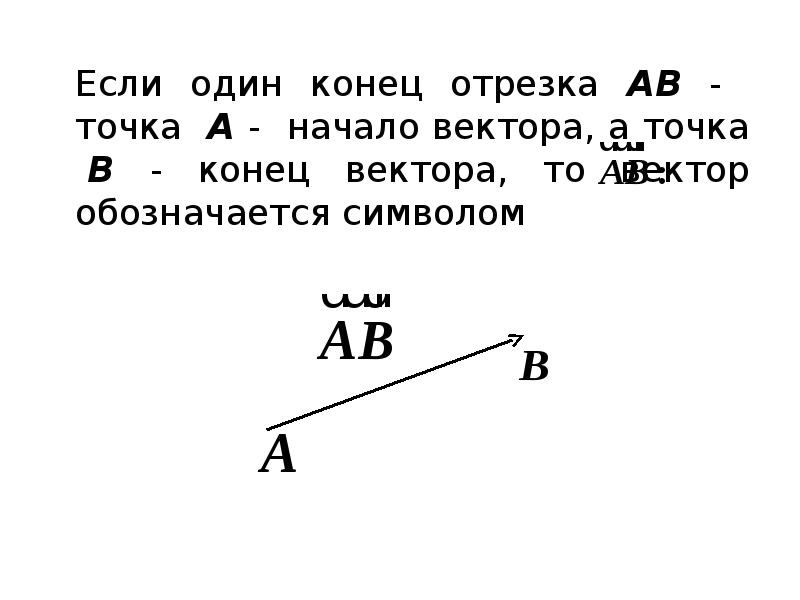
- 64. Если один конец отрезка AB - точка A - начало вектора,
- 65. Расстояние между началом и концом вектора называется его модулем (или длиной).
- 66. Векторы, лежащие на параллельных прямых (или на одной прямой), называются коллинеарными
- 67. Два коллинеарных вектора называются противоположными, если они имеют равные модули и
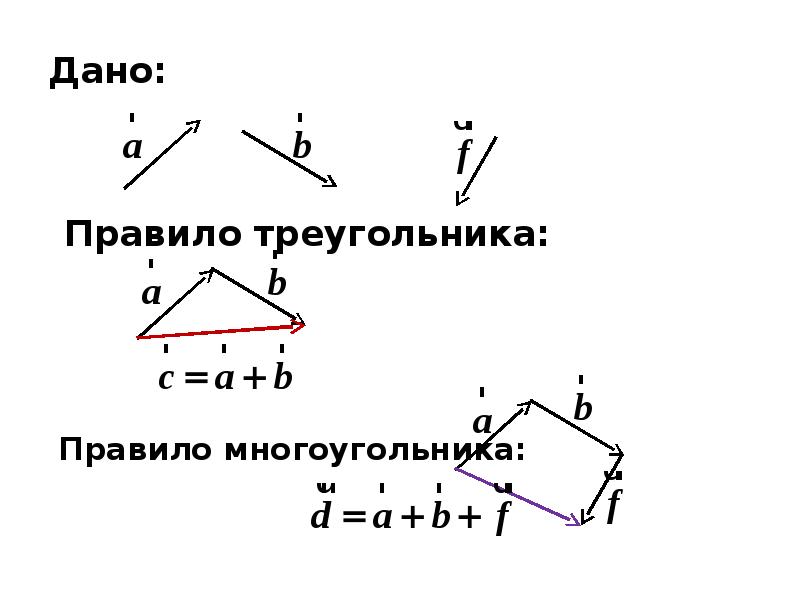
- 68. 1.2. Линейные операции над векторами Линейными операциями над векторами называют их
- 69. Дано: Дано:
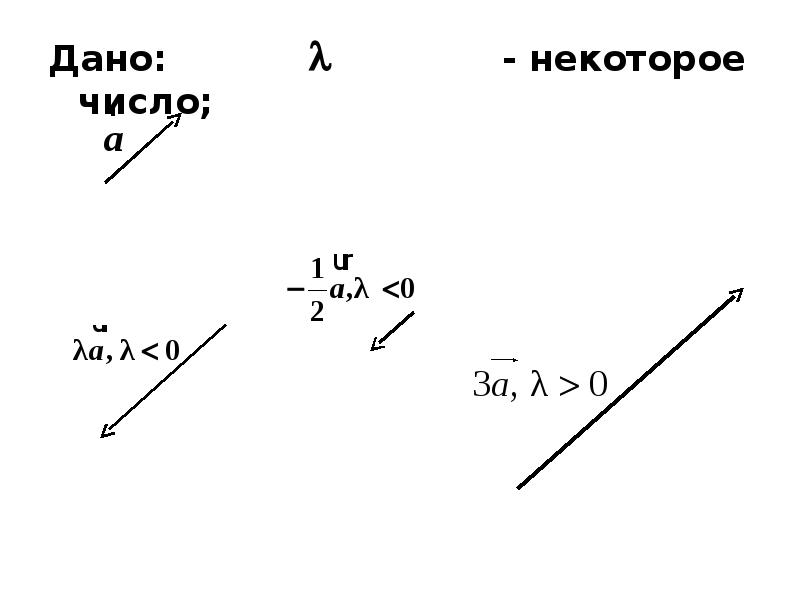
- 70. Умножение вектора на число Произведением вектора на число называется
- 71. Дано: - некоторое число; Дано:
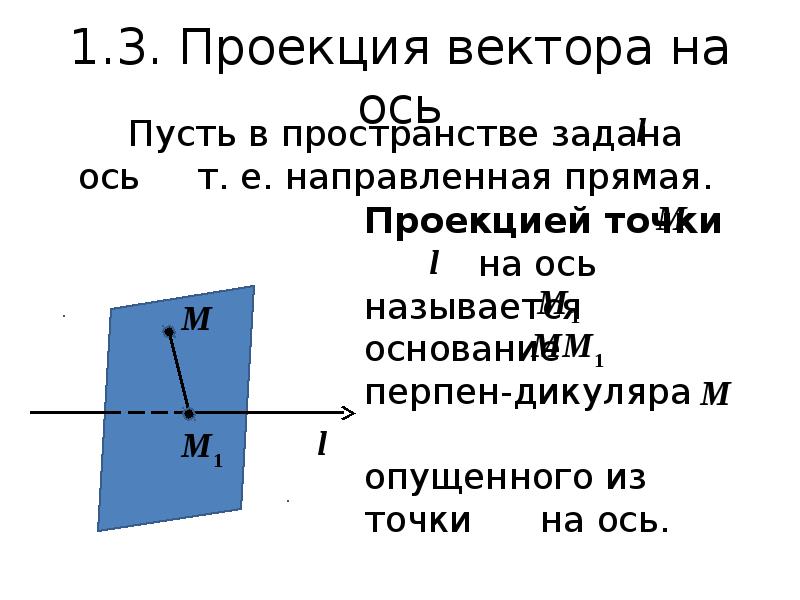
- 72. 1.3. Проекция вектора на ось Пусть в пространстве задана ось
- 73. Если точка M лежит на оси, то ее проекция на ось
- 74. Если точки и совпадают, то проекция вектора
- 75. 1.4. Линейная зависимость векторов При решении различных задач, как правило, приходится
- 76. ОПР. Линейной комбинацией векторов (1) называется вектор вида ОПР. Линейной комбинацией
- 77. ОПР. Система ненулевых векторов (1) называется линейно зависимой, если существую такие
- 78. ОПР. Размерностью системы векторов называется максимальное число содержащихся в нем линейно
- 79. Теорема Каждый вектор n-мерной системы векторов можно представить и
- 80. В силу единственности разложения (3) каждый вектор однозначно может быть определен
- 81. 1.5. Координаты вектора Координатами вектора в прямоугольной системе координат
- 82. Множество всех n-мерных векторов с действительными координатами обозначается Таким образом,
- 83. Если , – единичные векторы (орты) координатных осей, то
- 84. Если вектор имеет начало в точке Если вектор имеет
- 85. Пример Даны точки и
- 86. 1.6. Действия над векторами, заданными координатами Пусть тогда
- 87. Условие параллельности векторов и Условие параллельности векторов и
- 88. 1.7. Скалярное произведение векторов ОПР. Скалярным произведением векторов и
- 89. Свойства скалярного произведения: 1). 2). 3). 4).
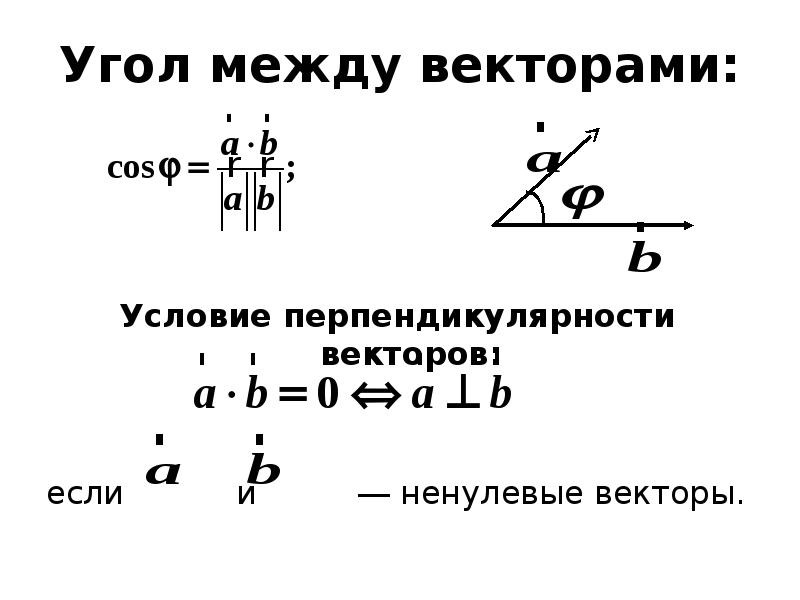
- 90. Угол между векторами: Условие перпендикулярности векторов: если и
- 91. Пример Найти скалярное произведение векторов И , если угол
- 92. Рассмотрим пространство Рассмотрим пространство Вектор Тогда
- 93. Компланарность векторов Три вектора компланарны тогда и только тогда, когда
- 94. Скачать презентацию














































































Слайды и текст этой презентации
Скачать презентацию на тему Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 2 семестр можно ниже:
Похожие презентации





























