Задача оптимизации. Проектные параметры презентация

Лекция 9 Основные понятия и определения задачи оптимизации Аналитические и численные методы решения задачи безусловной одномерной оптимизации Методы сканирования (прямого перебора) Метод деления отрезка пополам

Задача оптимизации. Проектные параметры Оптимизация – это процесс выбора наилучшего варианта из всех возможных. В инженерных расчетах методы оптимизации позволяют выбрать наилучший вариант конструкции, распределения ресурсов и т.п. В экономических расчетах – получить максимальную прибыль, добиться минимальных затрат и т.п. В процессе решения задачи оптимизации необходимо найти оптимальные значения проектных параметров (параметров плана), определяющих данную задачу: x1, x2, … xn. Содержательный смысл этих параметров зависит от конкретной задачи. Это могут быть линейные размеры, масса, температура и тому подобные параметры оптимизируемого объекта. Число n характеризует размерность задачи оптимизации.

Задача оптимизации. Целевая функция Выбор оптимального решения или сравнение альтернатив производится с помощью целевой функции f(x1, x2, … xn), зависящей от проектных параметров. Решение задачи оптимизации заключается в отыскании таких значений проектных параметров, при которых достигается минимум или максимум целевой функции. Примерами целевых функций могут служить мощность установки, прочность конструкции, объем выпуска продукции, стоимость перевозки грузов, прибыль и т.п. Геометрически целевая функция представляет собой поверхность в (n+1)–мерном пространстве. В частности, при n=1 это кривая на плоскости y=f(x); при n=2 – поверхность в 3–мерном пространстве y = f(x1, x2).

Безусловная и условная оптимизация Существует два типа задач оптимизации: безусловные и условные. Безусловная оптимизация – это отыскание минимума (максимума) функции и определение соответствующих значений аргументов в n–мерном пространстве без каких–либо ограничений на значения аргументов. Обычно рассматриваются задачи минимизации, так как задача отыскания максимума легко сводится к задаче минимизации путем замены знака целевой функции на противоположный. При условной оптимизации задача имеет ограничения, определяющие множество S в n–мерном пространстве, в пределах которого ищется оптимальное решение. Эти ограничения задаются совокупностью некоторых функций gi(x1, x2, … xn); i=1, 2, …m, удовлетворяющих уравнениям или неравенствам: gi(x1, x2, … xn) >= 0; i=1, 2, …m Теория и методы решения задач условной оптимизации – предмет исследования важного раздела прикладной математики – математического программирования.

Пример постановки задачи оптимизации

Пример постановки задачи оптимизации

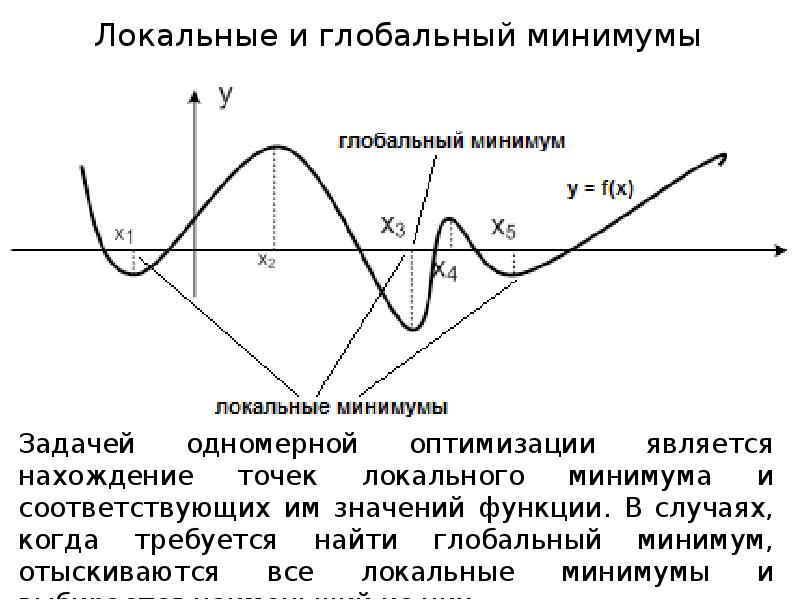
Локальные и глобальный минимумы

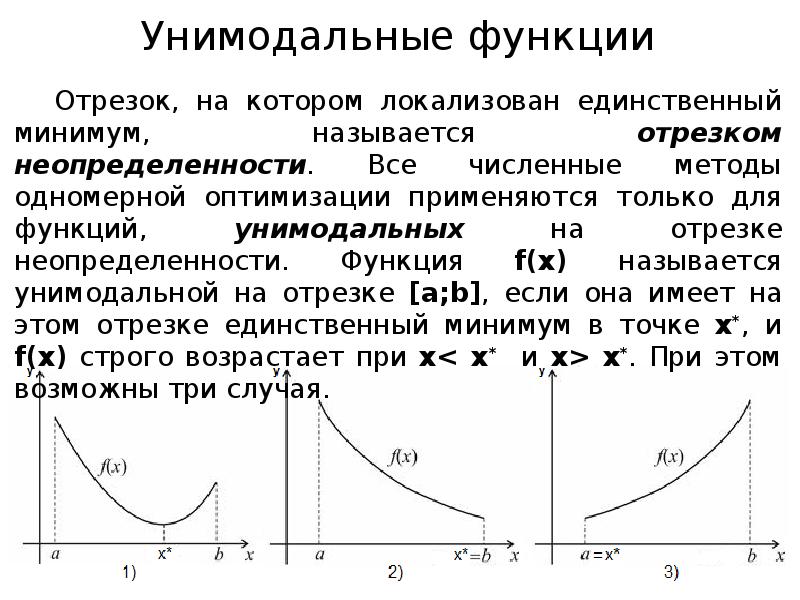
Унимодальные функции

Условия унимодальности функции Обычно при решении задачи одномерной оптимизации речь идет о поиске единственного экстремума функции. В этом случае необходимым условием унимодальности функции и существования экстремума является неубывание первой производной f'(x) на отрезке неопределенности [a;b]. Достаточным условием является положительный знак второй производной f''(x)>0 на отрезке неопределенности [a;b].

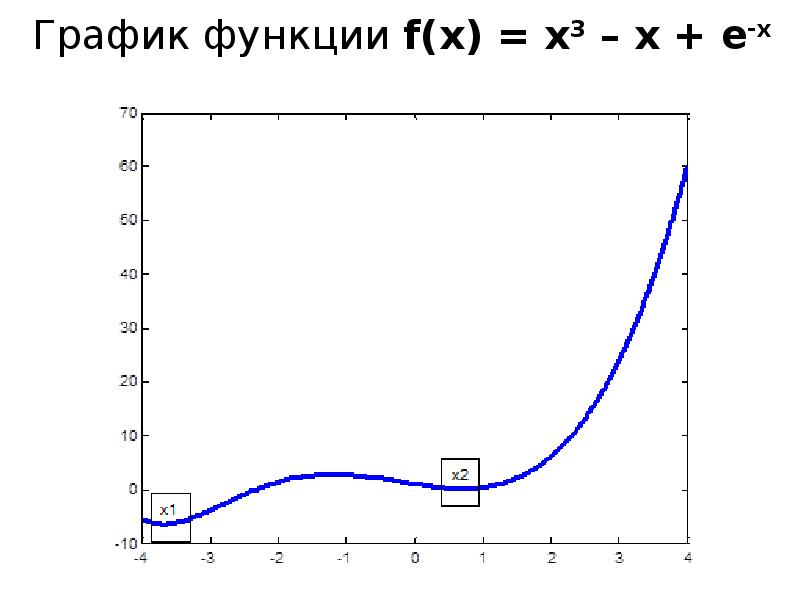
График функции f(x) = x3 – x + e-x

Пример проверки условий унимодальности

Аналитический метод отыскания локального минимума

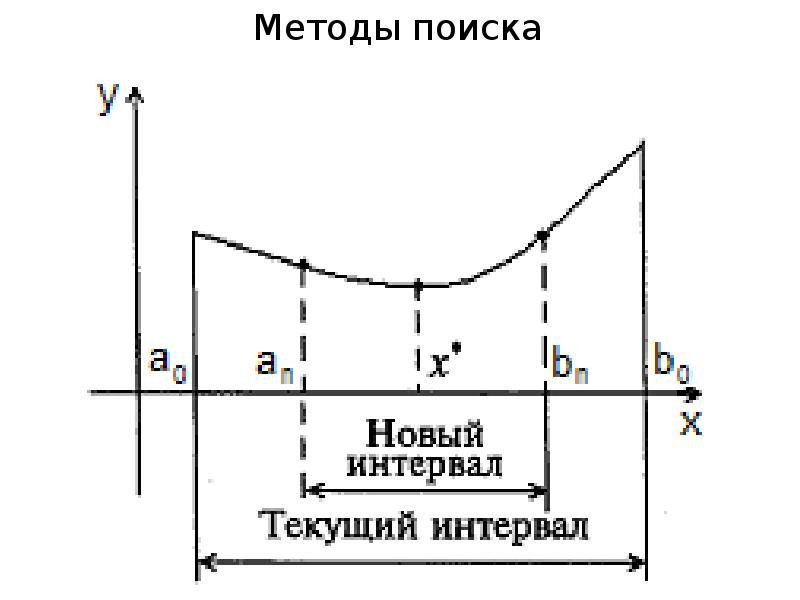
Методы поиска Для численного решения задачи безусловной одномерной оптимизации используются различные методы поиска. Их сущность состоит в последовательном сужении отрезка неопределенности. Вначале длина отрезка равна b0–a0, а в итоге она должна стать меньше заданной допустимой погрешности решения ε, так что х*ϵ[an;bn], причем bn - an < ε. За приближенное значение точки минимума ẍ может быть принята любая точка отрезка an;bn, при этом |ẍ - х*| <= bn - an < ε. Обычно принимают ẍ = (an+bn)/2, то есть середину отрезка.

Методы поиска

Методы сканирования (прямого перебора)

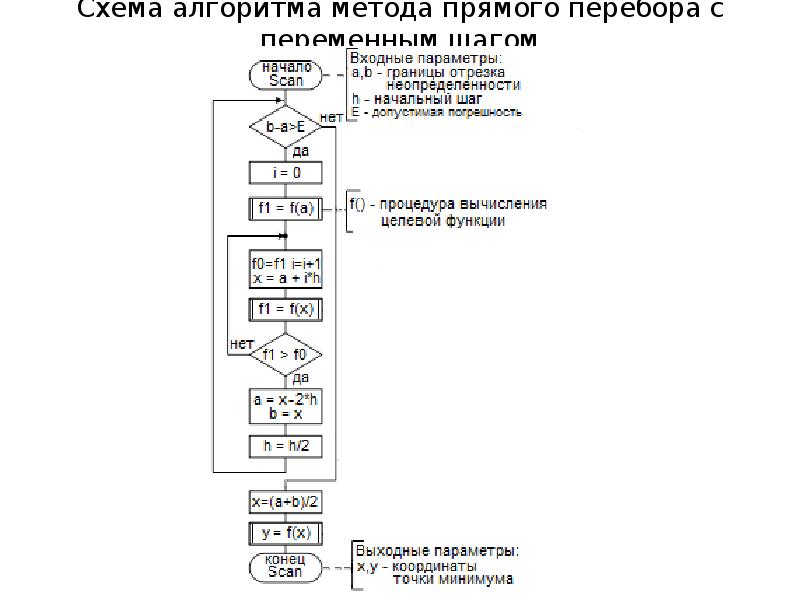
Схема алгоритма метода прямого перебора с переменным шагом

Методы последовательного поиска

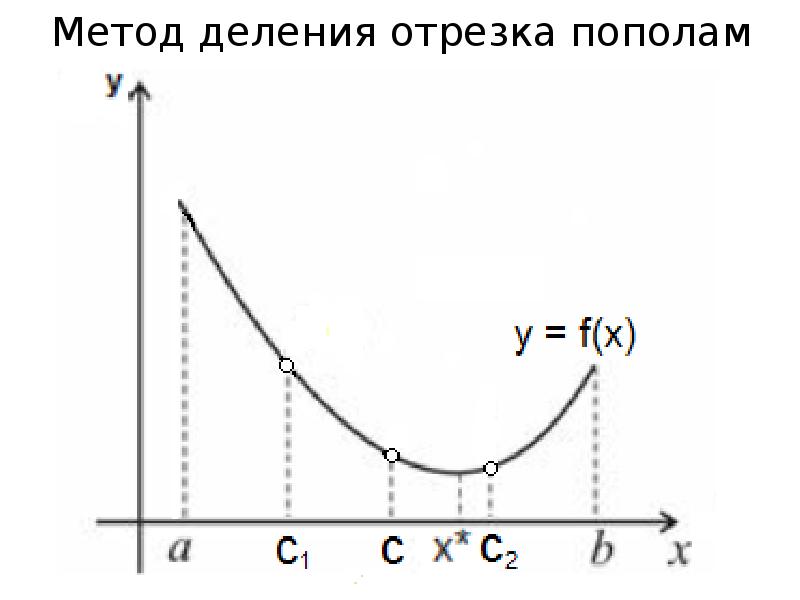
Метод деления отрезка пополам

Сущность метода деления отрезка пополам

Свойства метода деления отрезка пополам

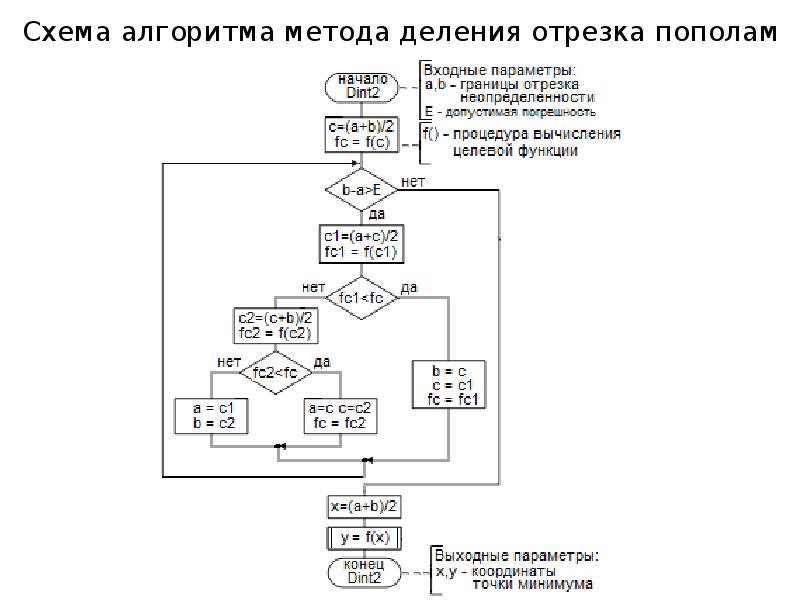
Схема алгоритма метода деления отрезка пополам