Методи розв’язування СЛАР (Система лінійних алгебраїчних рівнянь) презентация
Содержание
- 2. МЕТОДИ РОЗВ’ЯЗУВАННЯ СЛАР
- 4. ПРЯМІ МЕТОДИ РОЗВ’ЯЗУВАННЯ СЛАР МЕТОД ГАУССА
- 5. МЕТОД ГАУССА
- 6. МЕТОД ГАУССА
- 7. МЕТОД ГАУССА Метод Гаусса має сигнальну функцію виду (поліноміальний): Елемент
- 8. Матрицею перестановок P називається квадратна матриця, у якої в кожному рядку
- 9. З системи Ax = b маємо Cx = y З системи
- 10. Метод Гаусса відповідає розкладанню матриці A на добуток двох трикутних матриць:
- 11. LU-розкладання матриці А
- 12. Приклад
- 13. Схема Холецького
- 14. Обчислення det(A) на основі LU-розкладу матриці Обчислення det(A) на основі LU-розкладу
- 16. Обчислення A-1 Знаючи розклад обернену
- 17. РОЗВ’ЯЗУВАННЯ ПЕРЕВИЗНАЧЕНИХ СИСТЕМ РІВНЯНЬ Припустимо, що система Ax = b має
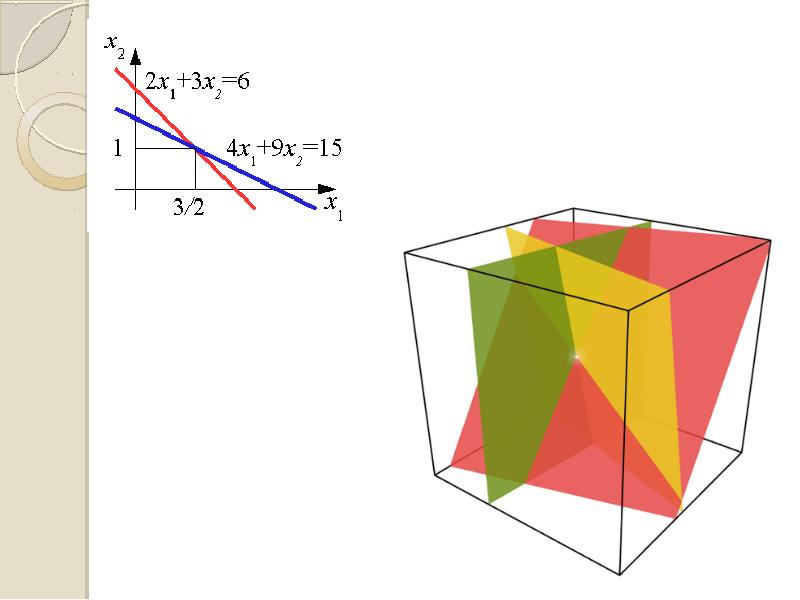
- 18. ТОЧНІСТЬ РОЗВ’ЯЗКУ СЛАР 6,1 x 1 + 3,4 x 2 =
- 20. Норми векторів Норма lp ||x||p = (|x1|p + |x2|p +…+|xn|p)1/p
- 21. Норми матриць Норма lp Евклидова норма Норма
- 22. ВЛАСТИВОСТІ НОРМ
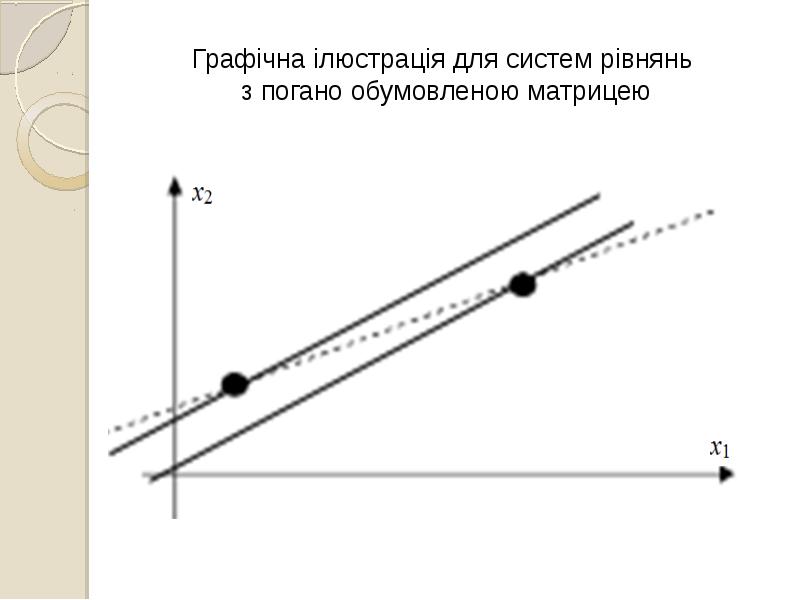
- 23. ЧИСЛО ОБУМОВЛЕНОСТІ
- 24. ЧИСЛО ОБУМОВЛЕНОСТІ
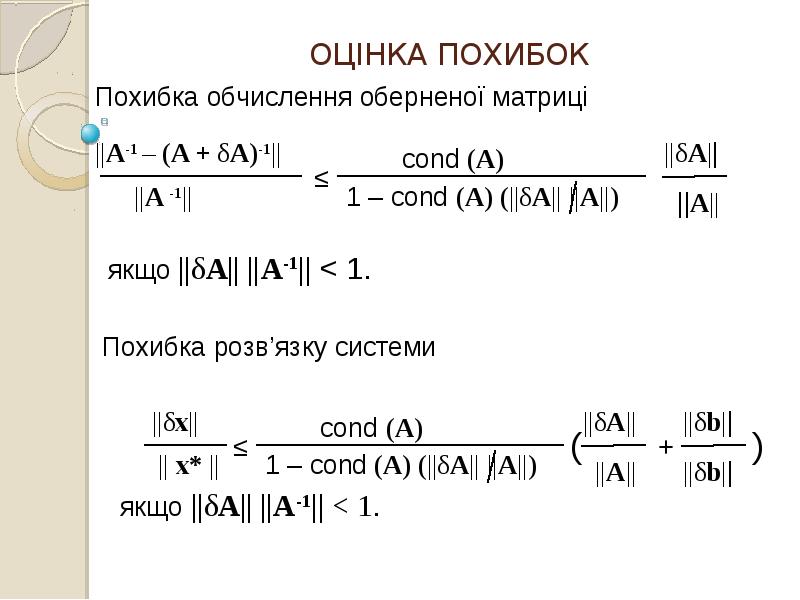
- 25. ОЦІНКА ПОХИБОК
- 26. ТОЧНІСТЬ РОЗВ’ЯЗКУ СЛАР 6,1 x 1 + 3,4 x 2 =
- 27. Скачать презентацию























Слайды и текст этой презентации
Скачать презентацию на тему Методи розв’язування СЛАР (Система лінійних алгебраїчних рівнянь) можно ниже:
Похожие презентации





























