Урок-лекция «Применение производной к исследованию и построению графиков функций» презентация
Содержание
- 2. Цель урока: научиться применять таблицу производных при исследовании функций и построении
- 3. Математический диктант
- 4. Классная работа Одной из основных задач, возникающих при исследовании функции, является
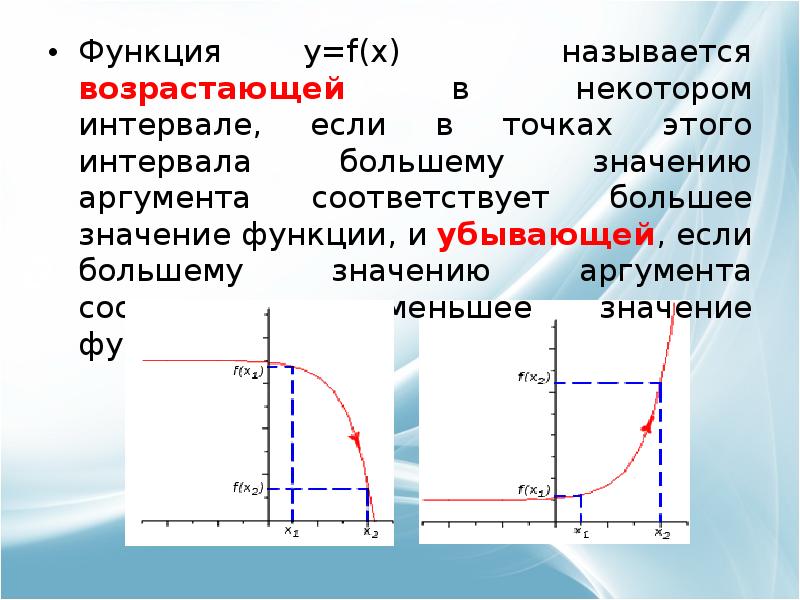
- 5. Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого
- 6. возрастающая возрастающая
- 7. Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная
- 8. Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция
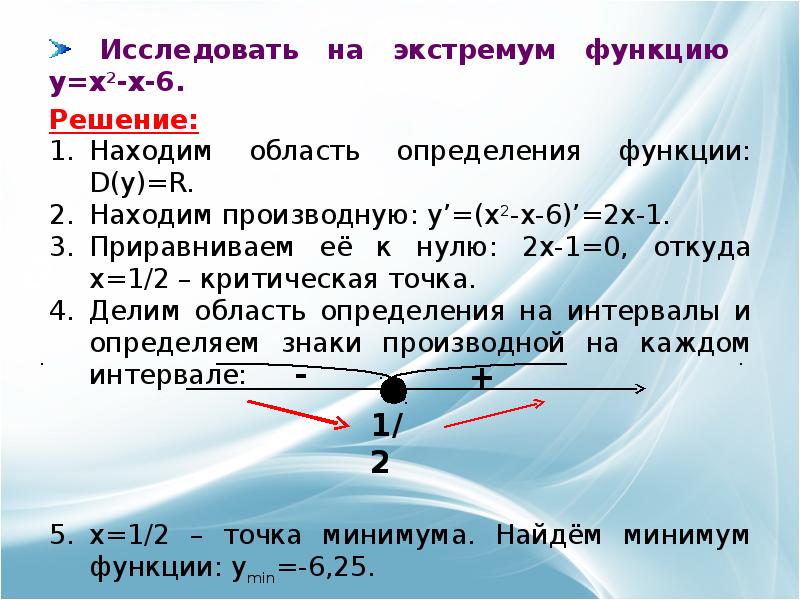
- 9. Находим область определения функции f(x). Находим область определения функции f(x). Вычисляем
- 10. Область определения: R. Функция непрерывна. Область определения: R. Функция непрерывна. Вычисляем
- 11. Область определения: R. Функция непрерывна. Область определения: R. Функция непрерывна. Вычисляем
- 12. Точку x=x0 называют точкой минимума функции y=f(x), если у этой точки
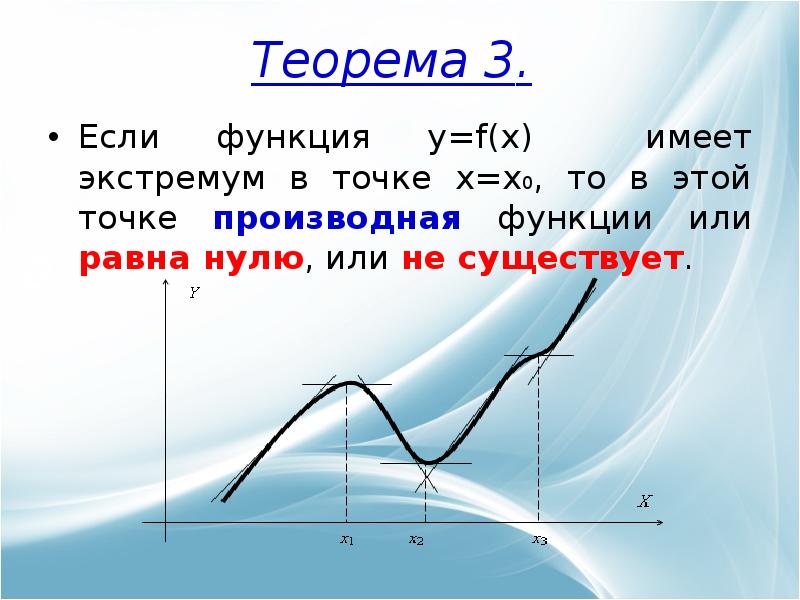
- 13. Если функция y=f(x) имеет экстремум в точке x=x0, то в этой
- 14. Если производная f’(x) при переходе через точку x0 меняет знак, то
- 15. Область определения: R. Функция непрерывна. Область определения: R. Функция непрерывна. Вычисляем
- 20. Скачать презентацию















Слайды и текст этой презентации
Скачать презентацию на тему Урок-лекция «Применение производной к исследованию и построению графиков функций» можно ниже:
Похожие презентации





























