Электростатика
Содержание
- 2. 2.1. Силовые линии электростатического поля 2.2. Поток вектора напряженности 2.3. Теорема
- 3. 2.1. Силовые линии электростатического поля Теорема Остроградского-Гаусса, которую мы докажем
- 4. Остроградский Михаил Васильевич (1801 – 1862) Остроградский Михаил Васильевич (1801 –
- 5. Гаусс Карл Фридрих (1777 – 1855) немецкий математик, астроном и физик.
- 6. Основная ценность теоремы Остроградского-Гаусса состоит в том, что она позволяет
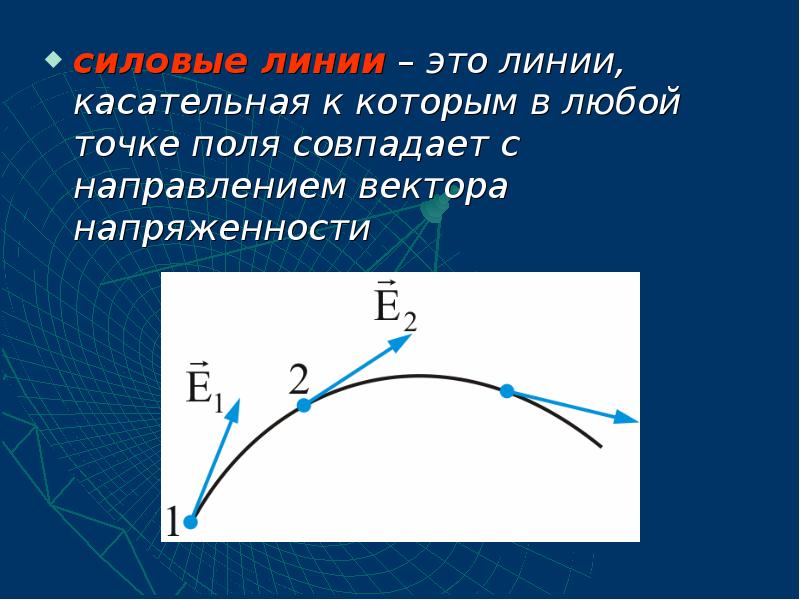
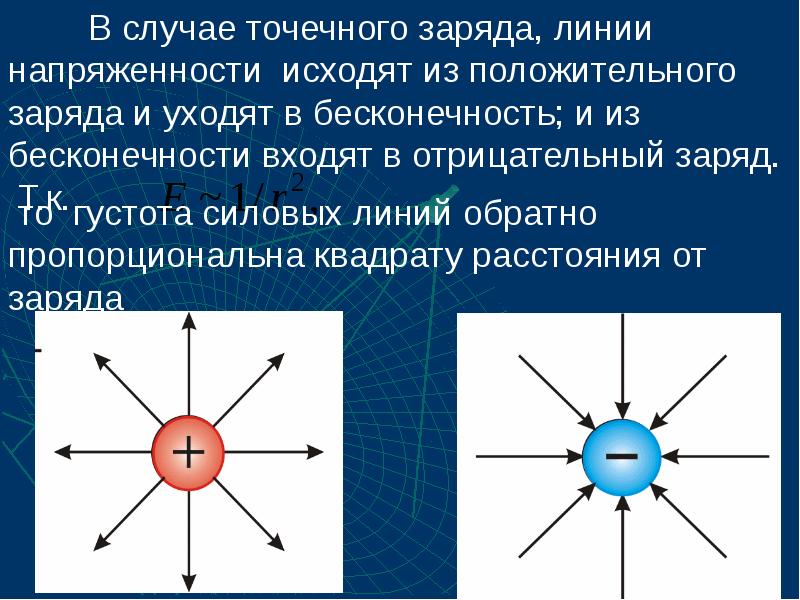
- 7. силовые линии – это линии, касательная к которым в любой точке
- 8. Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по
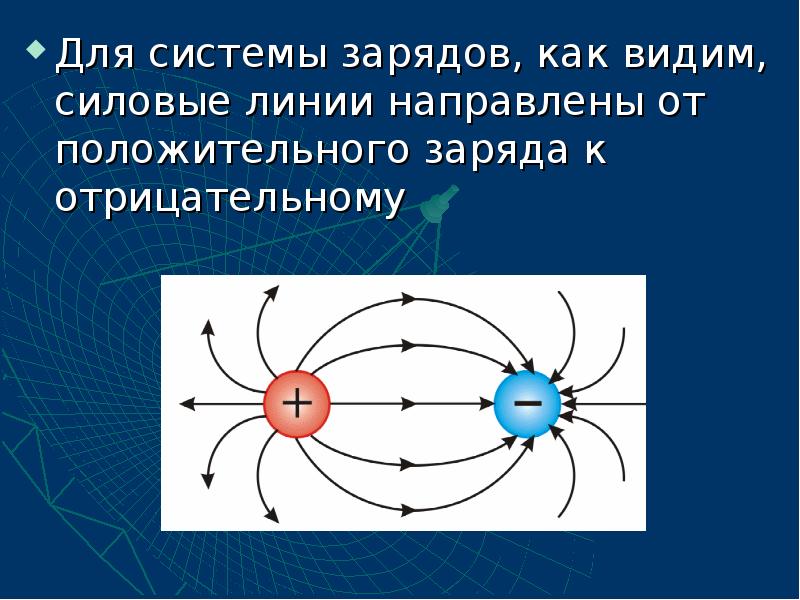
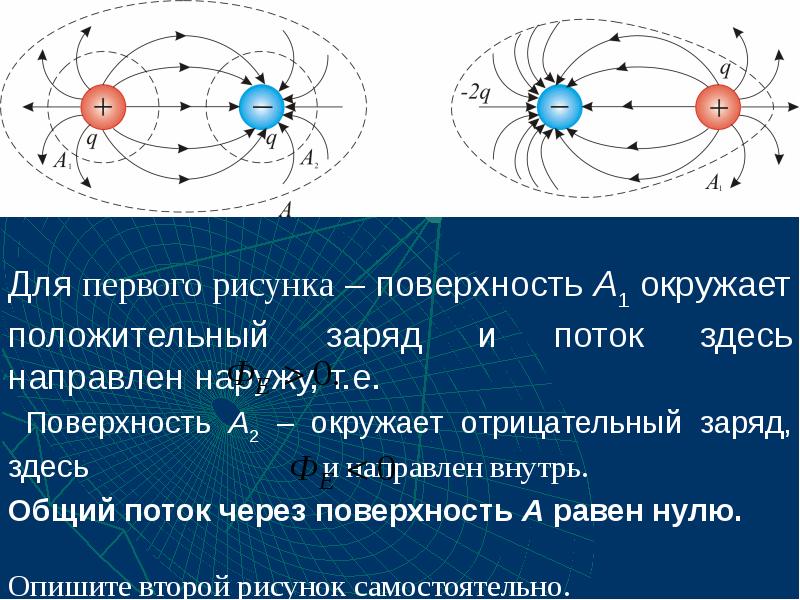
- 10. Для системы зарядов, как видим, силовые линии направлены от положительного заряда
- 12. Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к
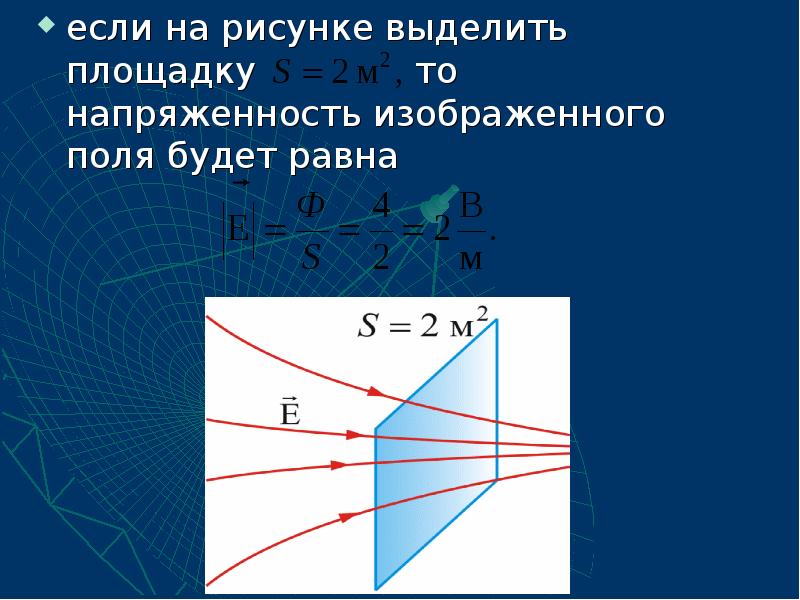
- 13. если на рисунке выделить площадку то напряженность изображенного
- 14. 2.2. Поток вектора напряженности Полное число силовых линий, проходящих через
- 15. Таким образом, поток вектора есть скаляр, который в зависимости от величины
- 17. 2.3. Теорема Остроградского-Гаусса Итак, по определению, поток вектора напряженности электрического
- 18. поток вектора напряженности через произвольную элементарную площадку dS будет равен: поток
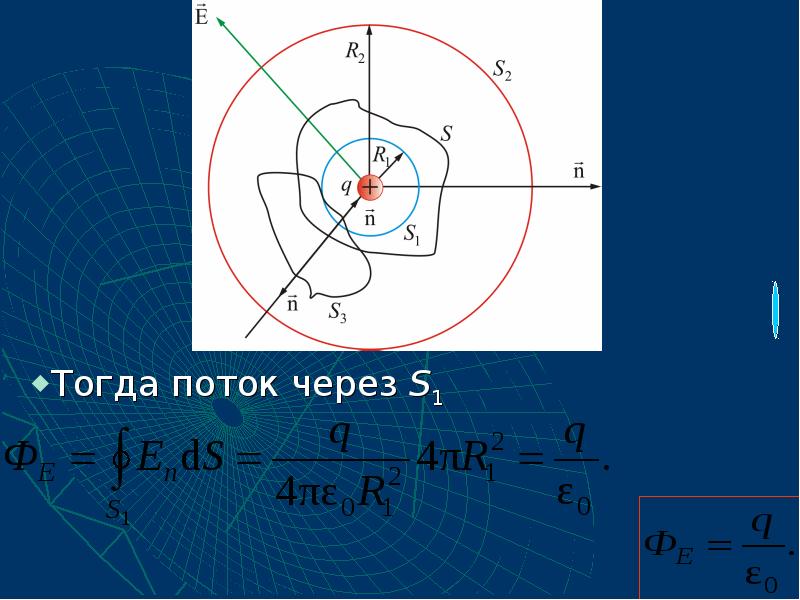
- 19. Подсчитаем поток вектора через произвольную замкнутую поверхность S, окружающую точечный заряд
- 20. Центр сферы совпадает с центром заряда. Радиус сферы S1 равен R1.
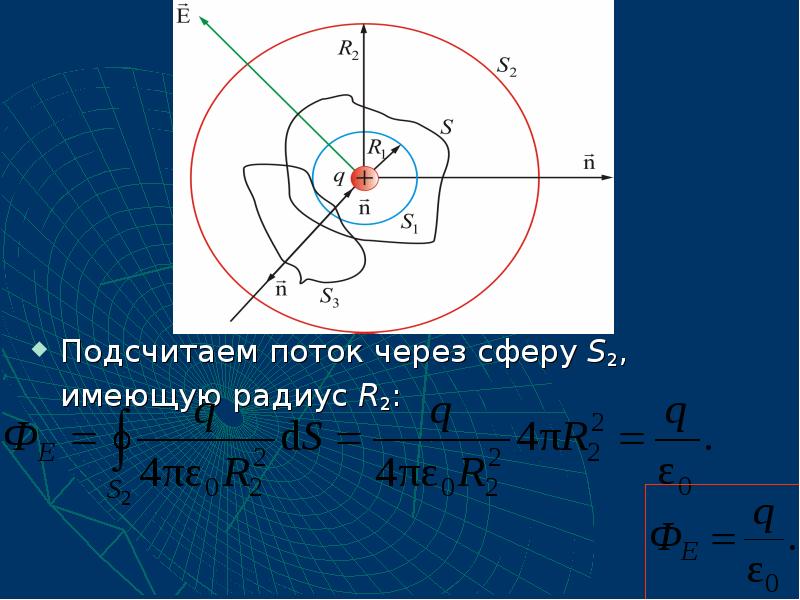
- 22. Подсчитаем поток через сферу S2, имеющую радиус R2:
- 23. Из непрерывности линии следует, что поток и через любую
- 24. Для любого числа произвольно расположенных зарядов, находящихся внутри поверхности: Для любого
- 26. Таким образом, для точечного заряда q, полный поток через любую замкнутую
- 27. Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в
- 28. Суммарный заряд объема dV будет равен: Суммарный заряд объема dV будет
- 29. 2.4. Дифференциальная форма теоремы Остроградского-Гаусса Пусть заряд распределен в пространстве
- 30. Теперь устремим , стягивая его к интересующей нас точке.
- 31. Дивергенция поля Е Дивергенция поля Е
- 32. Итак, Итак,
- 33. Сам по себе оператор смысла не имеет. Он приобретает смысл в
- 34. В тех точках поля, где – (положительные заряды)
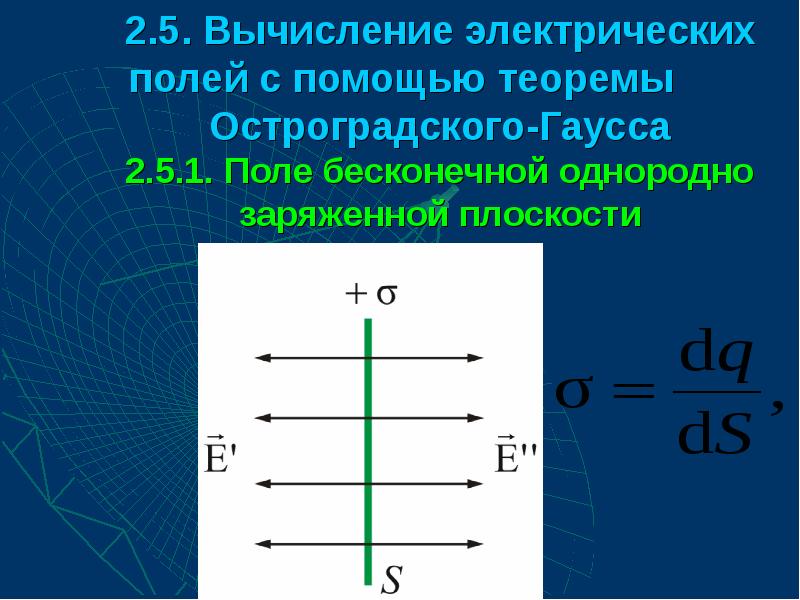
- 35. 2.5. Вычисление электрических полей с помощью теоремы Остроградского-Гаусса 2.5.1. Поле
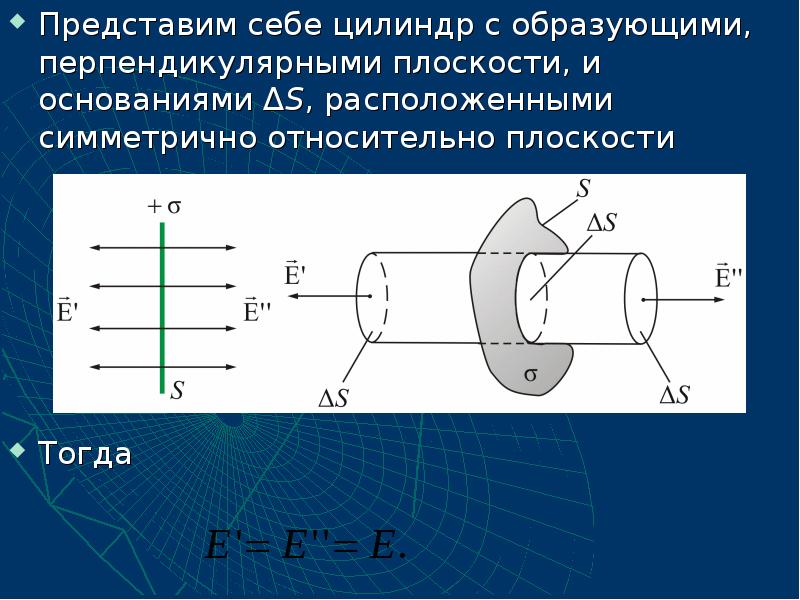
- 37. Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными
- 38. Суммарный поток через замкнутую поверхность (цилиндр) будет равна: Суммарный поток через
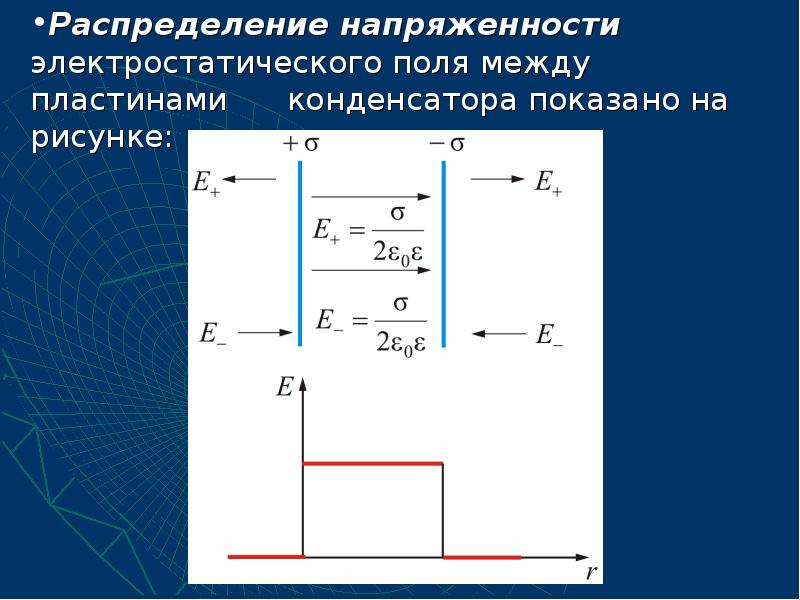
- 39. 2.5.2. Поле двух равномерно заряженных плоскостей Пусть две бесконечные плоскости
- 40. Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых
- 42. Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
- 43. Сила притяжения между пластинами конденсатора: Сила притяжения между пластинами конденсатора:
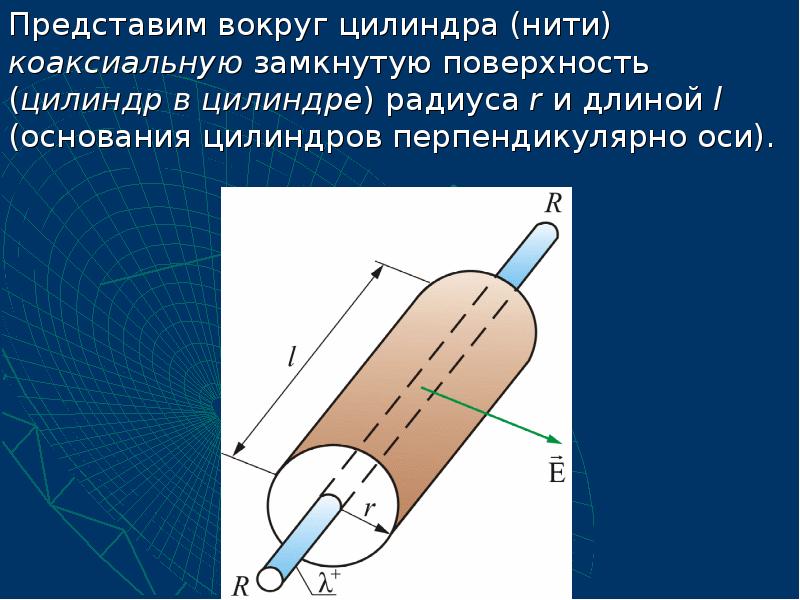
- 44. 2.5.3. Поле заряженного бесконечного цилиндра (нити) Пусть поле создается бесконечной
- 46. Для оснований цилиндров Для оснований цилиндров
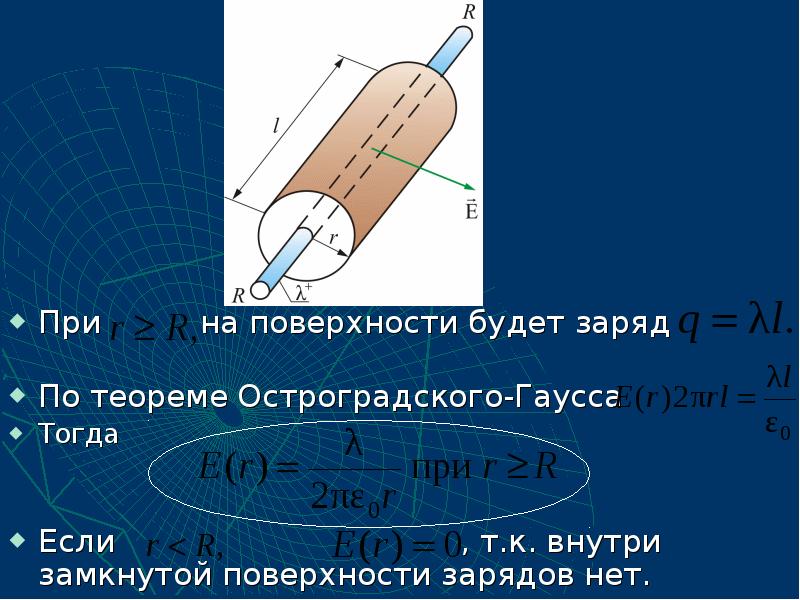
- 47. При на поверхности будет заряд По
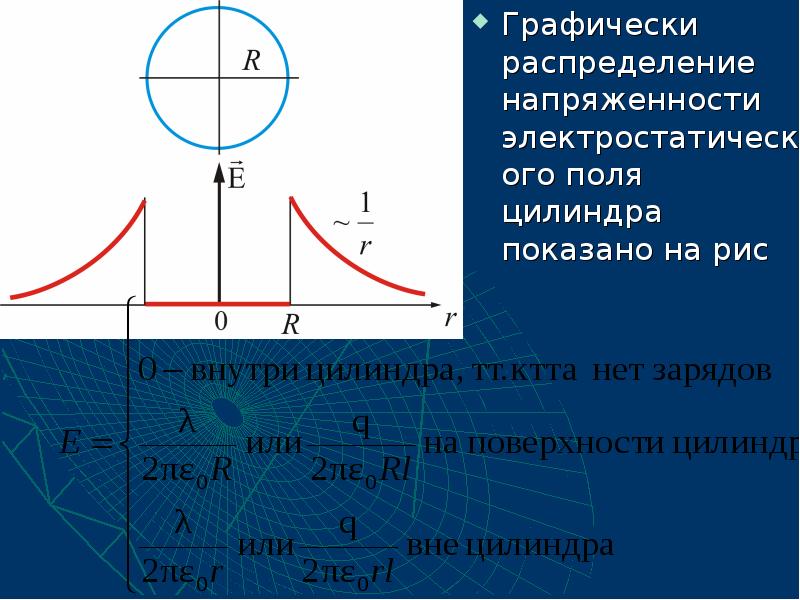
- 48. Графически распределение напряженности электростатического поля цилиндра показано на рис Графически распределение
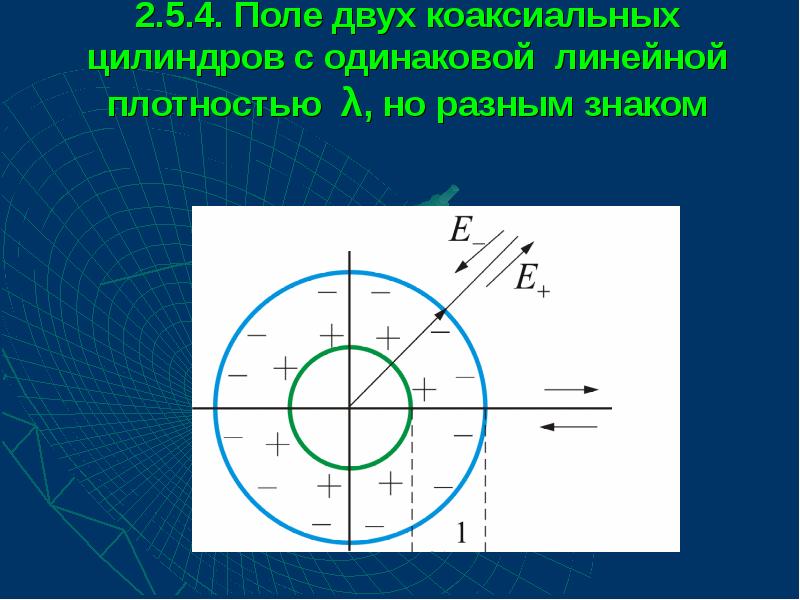
- 49. 2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но
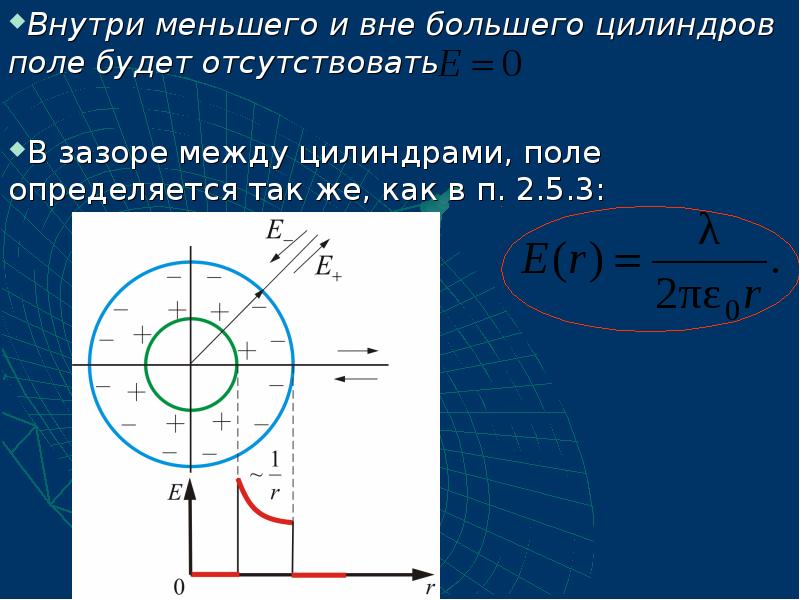
- 51. Таким образом для коаксиальных цилиндров имеем: Это справедливо и для бесконечно
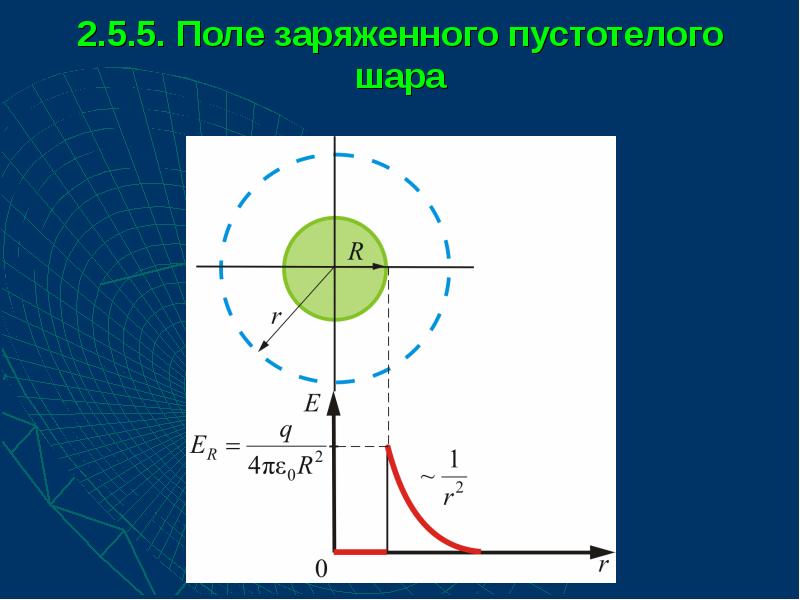
- 52. 2.5.5. Поле заряженного пустотелого шара
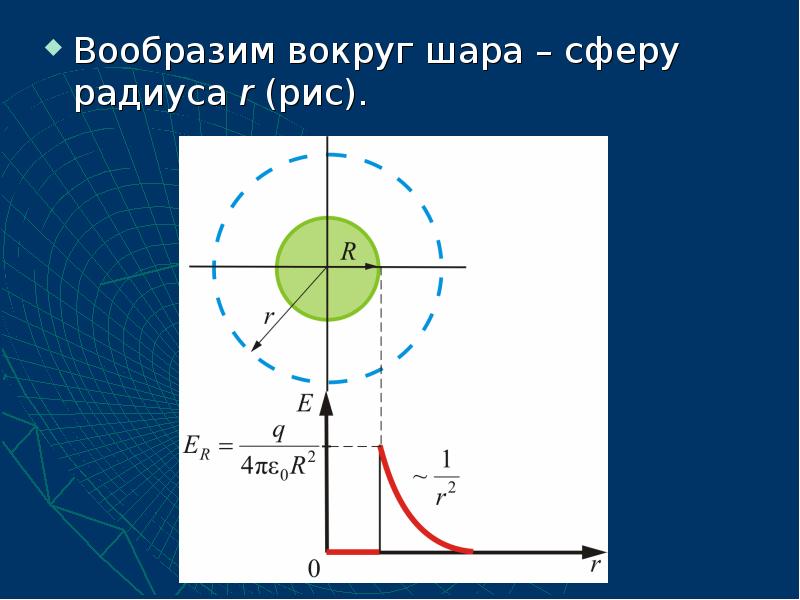
- 53. Вообразим вокруг шара – сферу радиуса r (рис). Вообразим вокруг шара
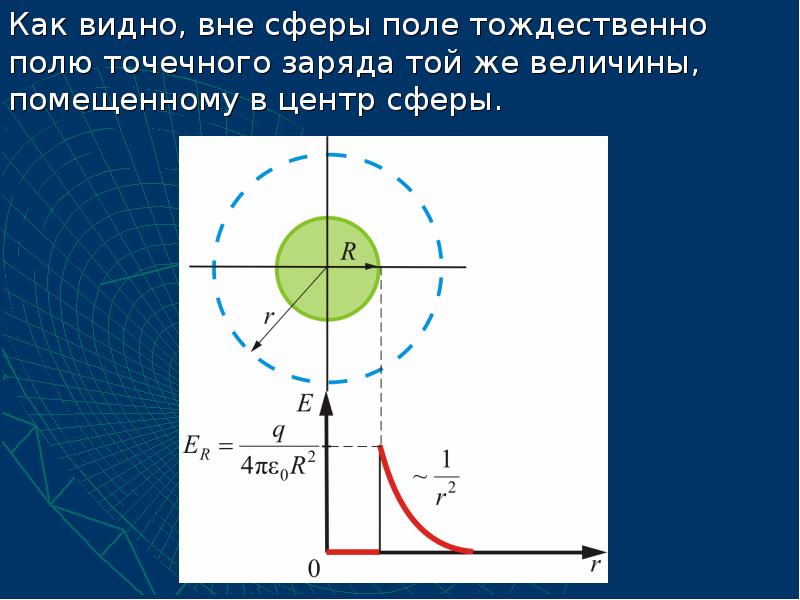
- 54. Если то внутрь воображаемой сферы попадет весь заряд q,
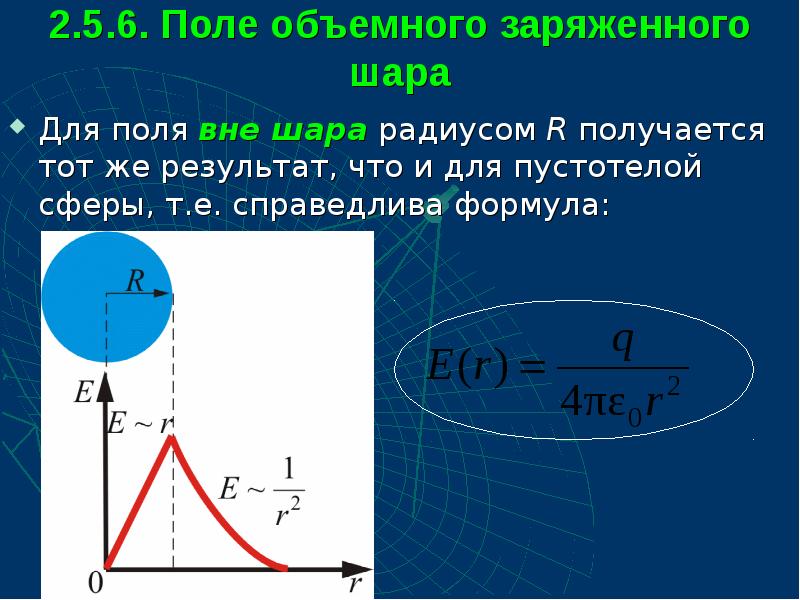
- 56. 2.5.6. Поле объемного заряженного шара Для поля вне шара радиусом
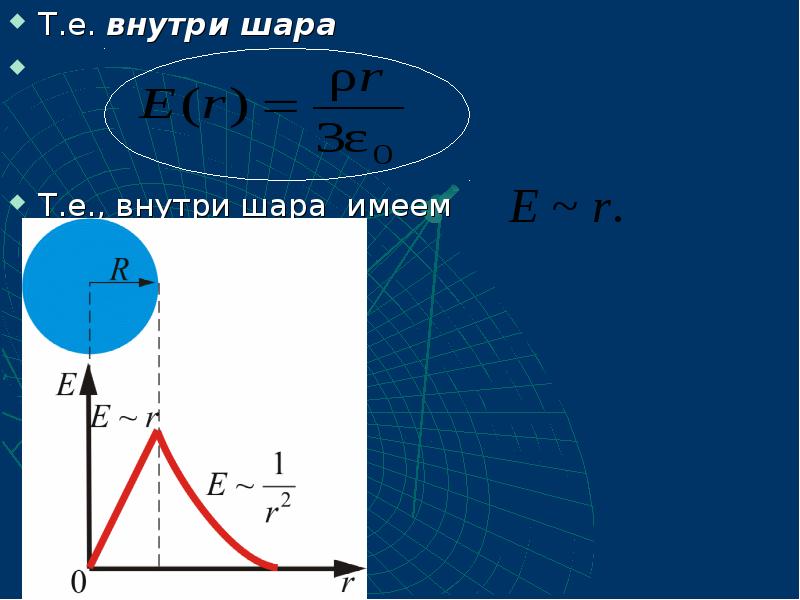
- 57. Внутри шара при сферическая поверхность будет содержать в себе
- 58. Т.е. внутри шара Т.е. внутри шара
- 59. Таким образом, имеем: поле объемного заряженного шара
- 61. Скачать презентацию






































Слайды и текст этой презентации
Похожие презентации