Удивительный мир многогранников презентация

Введение С многогранниками мы постоянно встречаемся в жизни – это древние египетские пирамиды и кубики, которыми играют дети, объекты архитектуры и дизайна, природные кристаллы, вирусы, которые можно рассмотреть только в электронный микроскоп и т.д. Многогранник – это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности, общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани плоского выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника. Правильные и звездчатые многогранники с древних времен привлекали к себе внимание ученых, архитекторов, художников, их поражала красота, гармония и совершенство этих многогранников.

Исторические сведения Правильные многогранники с древних времен привлекали к себе внимание ученых, архитекторов, художников. Их поражала красота, совершенство, гармония этих многогранников. Леонардо да Винчи увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал книгу монаха Луки Пачоли «О божественной пропорции». Другим знаменитым художником, также увлекавшимся геометрией был Альбрехт Дюрер. В своей гравюре «Меланхолия» он дал перспективное изображение додекаэдра. Немецкий астроном и математик Иоганн Кеплер в своей работе, используя правильные многогранники, вывел принцип которому подчиняются формы и размеры планет Солнечной системы. Такая модель получила модель «Космического кубка» Кеплера. Знаменитая картина Сальвадора Дали «Тайная вечеря» содержит перспективное изображение правильного додекаэдра. В знаменитом соборе в Солсбери столько интересных реликвий, что лишь немногие посетители бросят взгляд на надгробие Томаса Горджеса, усопшего в 1610 году. А между тем резьба на могильном камне содержит изображения додекаэдра, трех икосаэдров и двух кубооктаэдров. На камне вырезаны скелетные каркасы этих тел в манере, близкой к использованной Леонардо да Винчи при построении моделей однородных многогранников с каркасом из прутьев.

Кристаллы – природные многогранники Многие формы многогранников изобрел не человек, а создала природа в виде кристаллов. Например, кристаллы поваренной соли имеют форму куба, кристаллы льда и горного хрусталя (кварца) напоминают отточенный с двух сторон карандаш, то есть форму шестиугольной призмы, на основании которой поставлены шестиугольные пирамиды. Алмаз чаще всего встречается в виде октаэдра, иногда куба и даже кубооктаэдра. Исландский шпат, который раздваивает изображение, имеет форму косого параллелепипеда; гранат – ромбододекаэдр (двенадцатигранника), у которого все грани ромбы.

Правильные многогранники Тела Платона Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэролл. С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам - удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны.

Тетраэдр Наиболее простым правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники. У тетраэдра 6 ребер, 4 грани и 4 вершины. Платон связывает тетраэдр со стихией огня.

Октаэдр Октаэдр – многогранник, гранями которого являются правильные треугольники. Его поверхность состоит из 8 правильных треугольников. У октаэдра 12 ребер, 8 граней и 6 вершин. Платон связывает октаэдр со стихией воздуха.

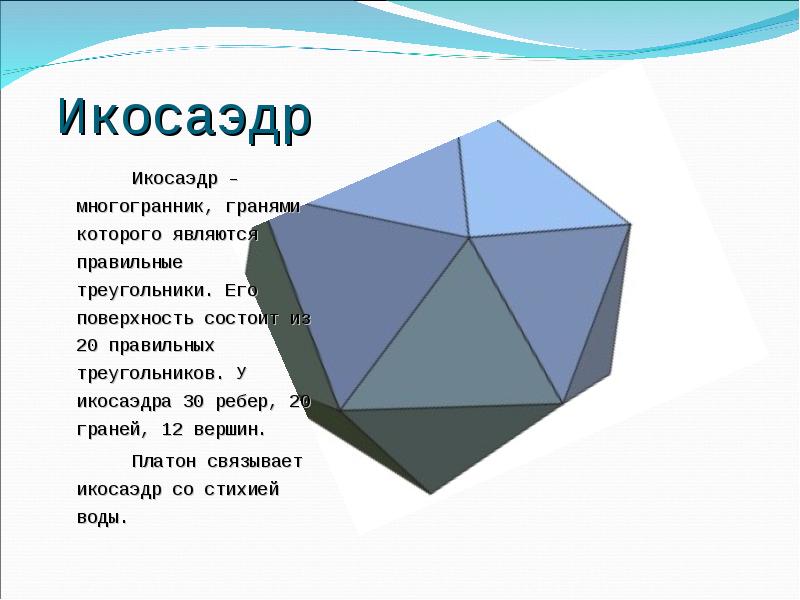
Икосаэдр Икосаэдр – многогранник, гранями которого являются правильные треугольники. Его поверхность состоит из 20 правильных треугольников. У икосаэдра 30 ребер, 20 граней, 12 вершин. Платон связывает икосаэдр со стихией воды.

Гексаэдр Гексаэдр – многогранник гранями которого являются правильные четырехугольники (квадраты). Его поверхность состоит из 12 ребер, 6 граней и 8 вершин. Платон связывает гексаэдр (куб) со стихией земли.

Додекаэдр Додекаэдр – многогранник, гранями которого являются правильные пятиугольники. Его поверхность состоит из 30 ребер, 12 граней и 20 вершин. Платон в своей идеалистической картине мира считает додекаэдр моделью всей Вселенной.

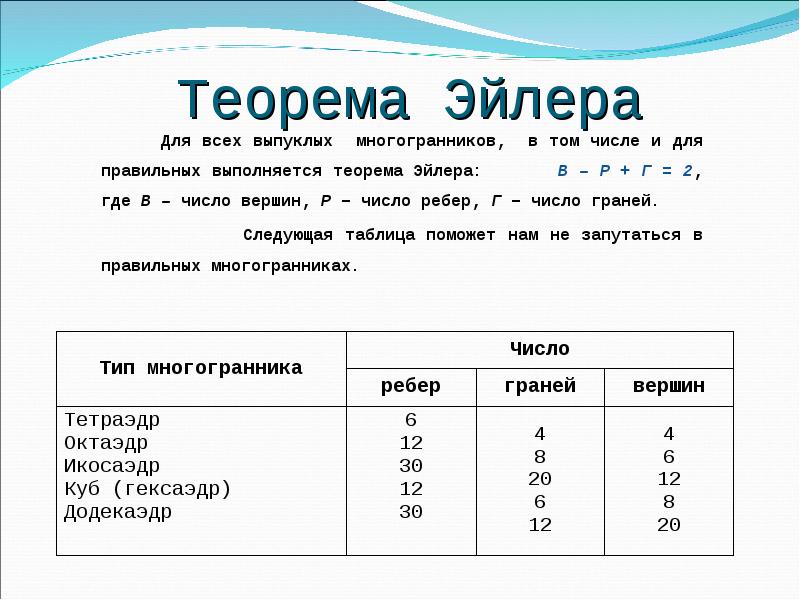
Теорема Эйлера Для всех выпуклых многогранников, в том числе и для правильных выполняется теорема Эйлера: В – Р + Г = 2, где В – число вершин, Р – число ребер, Г – число граней. Следующая таблица поможет нам не запутаться в правильных многогранниках.

Звездчатые многогранники Тела Кеплера – Пуансо Из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники. Их всего четыре, они называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр

Малый звездчатый додекаэдр Возьмем додекаэдр. Продолжение его ребер приводит к замене каждой грани звездчатым правильным пятиугольником, и в результате возникает многогранник, который называется малым звездчатым додекаэдром.

Большой додекаэдр При продолжении граней додекаэдра возникает 2 возможности. Если в качестве граней рассматривать правильные пятиугольники, то получится большой додекаэдр.

Большой звездчатый додекаэдр Если в качестве граней рассматривать звездчатые пятиугольники, то получится большой звездчатый додекаэдр.

Большой икосаэдр Икосаэдр имеет одну звездчатую форму. При продолжении граней правильного икосаэдра получается большой икосаэдр.

Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч разных типов снежинок! Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч разных типов снежинок!

Звездчатые многогранники Кроме правильных звездчатых многогранников существуют звездчатые многогранники, полученные из полуправильных многогранников, которые не менее красивы, оригинальны и гармоничны. В настоящее время известны 51 вид таких многогранников. Вот некоторые из них:

Звезда

Квазиусеченный звездчатый додекаэдр

Квазиусеченный гексаэдр

Битригональный додекаэдр

Заключение В своей работе «Удивительный мир многогранников» я попыталась открыть не только свойства геометрических тел, но и красоту, и гармонию многогранников. Благодаря многогранникам открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии. Мне так же удалось построить несколько моделей тел Кеплера - Пуансо. Также я приобрела опыт работы с литературой, научилась выбирать необходимую информацию. Над этой темой я работаю второй год. И не собираюсь останавливаться на достигнутом! Тела Платона (правильные многогранники), тела Кеплера Пуансо (звездчатые многогранники) – это всего лишь песчинка в необъятном океане многогранных форм.