Введение в теорию графов презентация

Введение в теорию графов

Введение С дворянским титулом «граф» тему моей работы связывает только общее происхождение от латинского слова «графио» - пишу.

Что такое граф Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. В процессе решения задач математики заметили, что удобно изображать объекты точками, а отношения между ними отрезками или дугами.

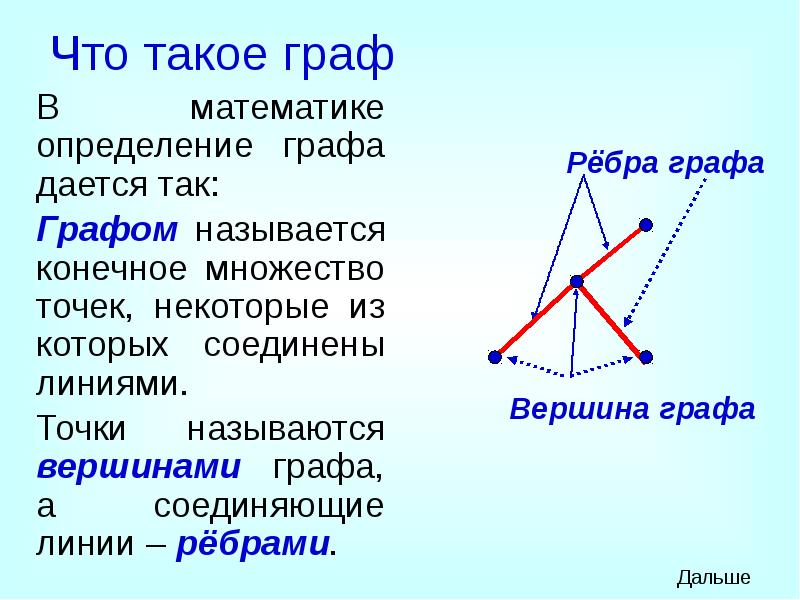
Что такое граф В математике определение графа дается так: Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами.

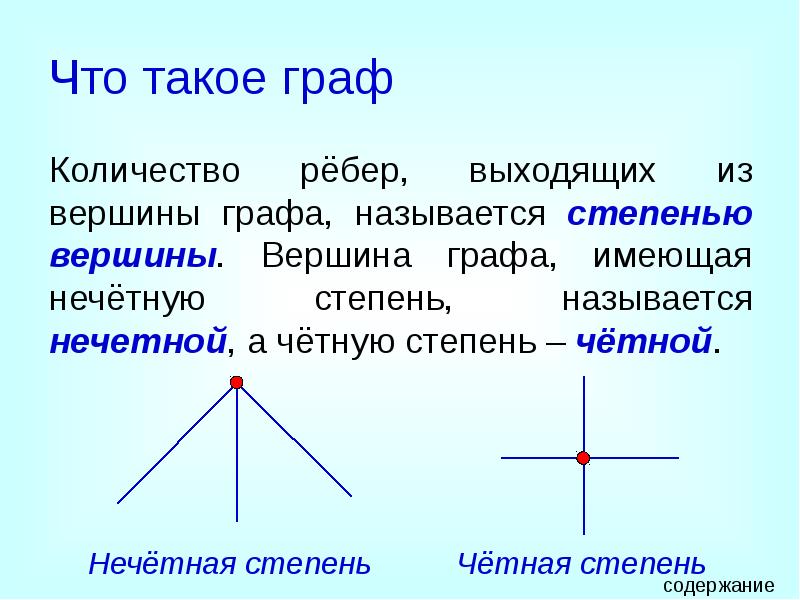
Что такое граф Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.

История возникновения графов Термин "граф" впервые появился в книге венгерского математика Д. Кенига в 1936 г., хотя начальные важнейшие теоремы о графах восходят к Л. Эйлеру.

История возникновения графов Основы теории графов как математической науки заложил в 1736 г. Леонард Эйлер, рассматривая задачу о кенигсбергских мостах. Сегодня эта задача стала классической.

Задача о Кенигсбергских мостах Бывший Кенигсберг (ныне Калининград) расположен на реке Прегель. В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены.

Задача о Кенигсбергских мостах Кенигсбергцы предлагали приезжим следующую задачу: пройти по всем мостам и вернуться в начальный пункт, причём на каждом мосту следовало побывать только один раз.

Задача о Кенигсбергских мостах Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.

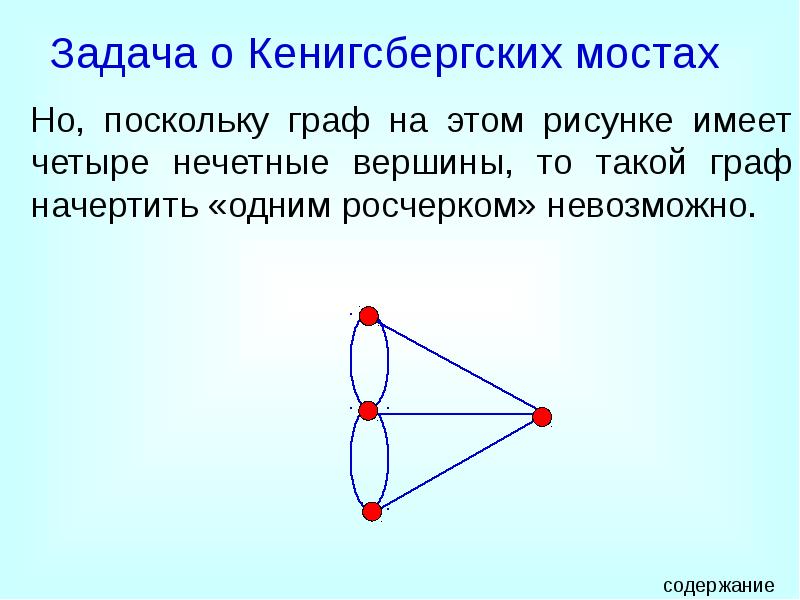
Задача о Кенигсбергских мостах Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой граф начертить «одним росчерком» невозможно.

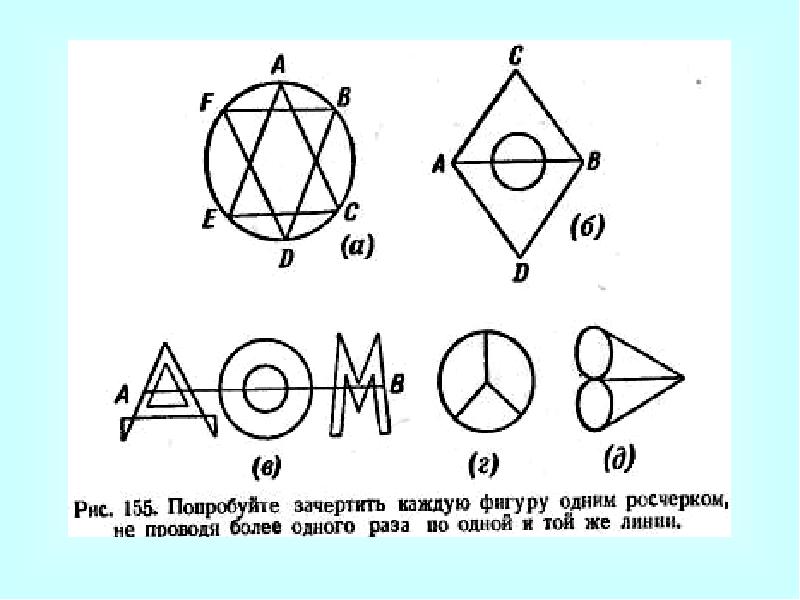
Одним росчерком Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа: Невозможно начертить граф с нечетным числом нечетных вершин.

Одним росчерком Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.

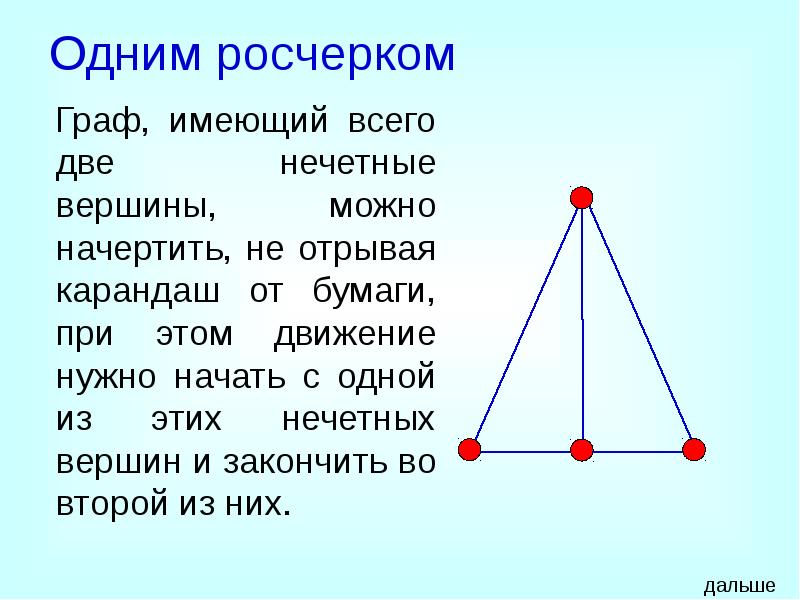
Одним росчерком Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.

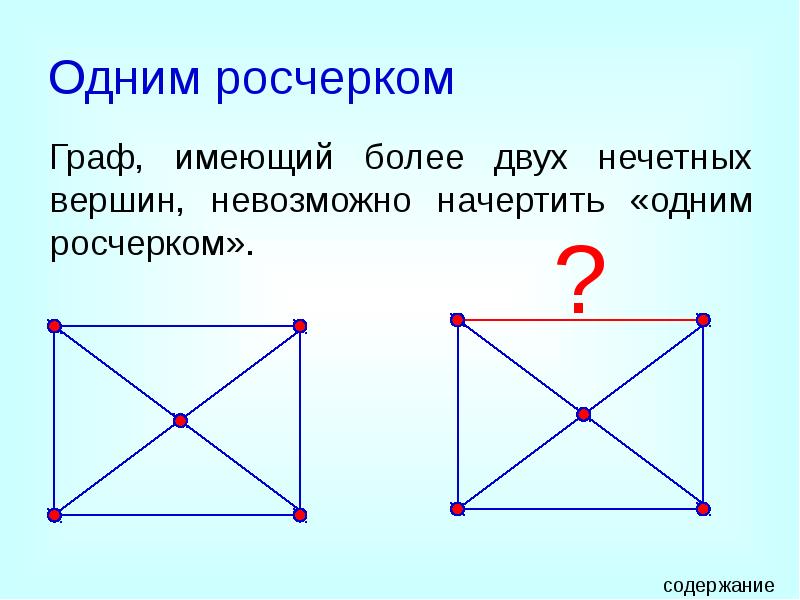
Одним росчерком Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».

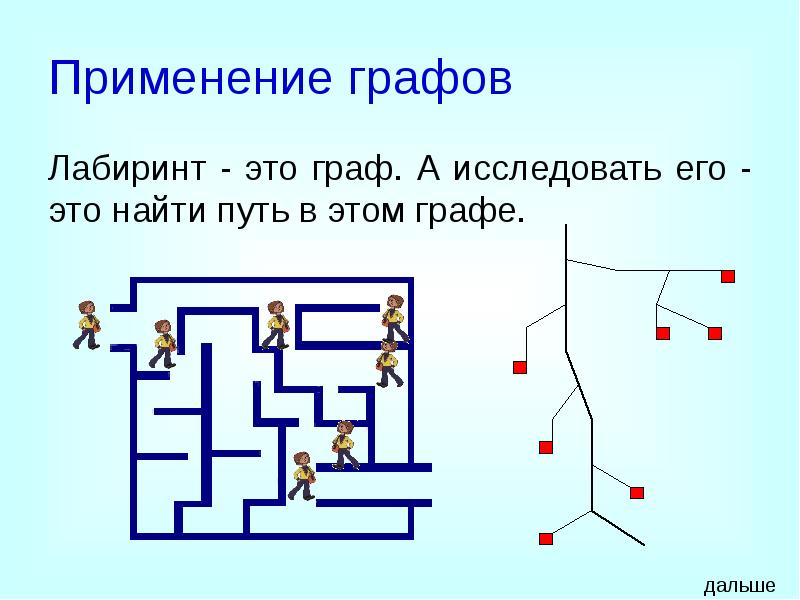
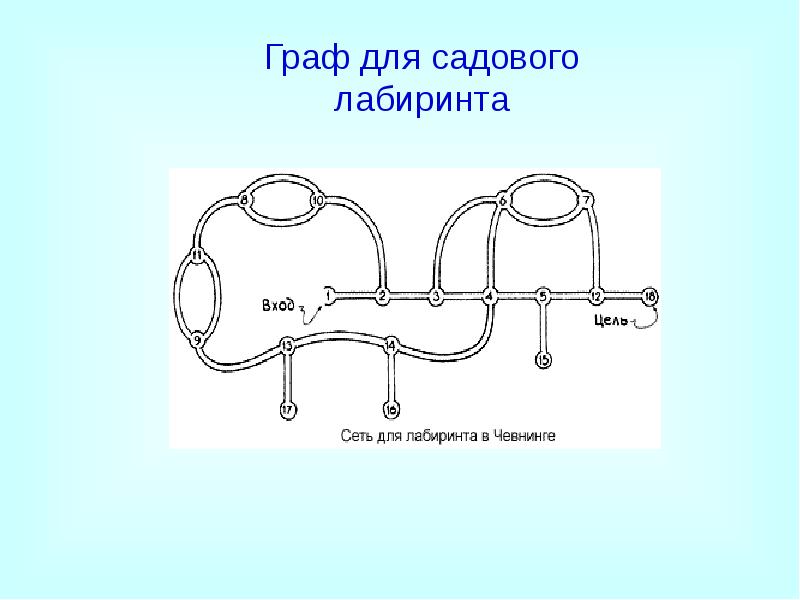
Применение графов Лабиринт - это граф. А исследовать его - это найти путь в этом графе.

Выводы Графы – это замечательные математические объекты, с помощью, которых можно решать математические, экономические и логические задачи. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Графы используются при составлении карт и генеалогических древ. В математике даже есть специальный раздел, который так и называется: «Теория графов».

Применение графов Использует графы и дворянство. На рисунке приведена часть генеалогического дерева знаменитого дворянского рода Л. Н. Толстого. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.

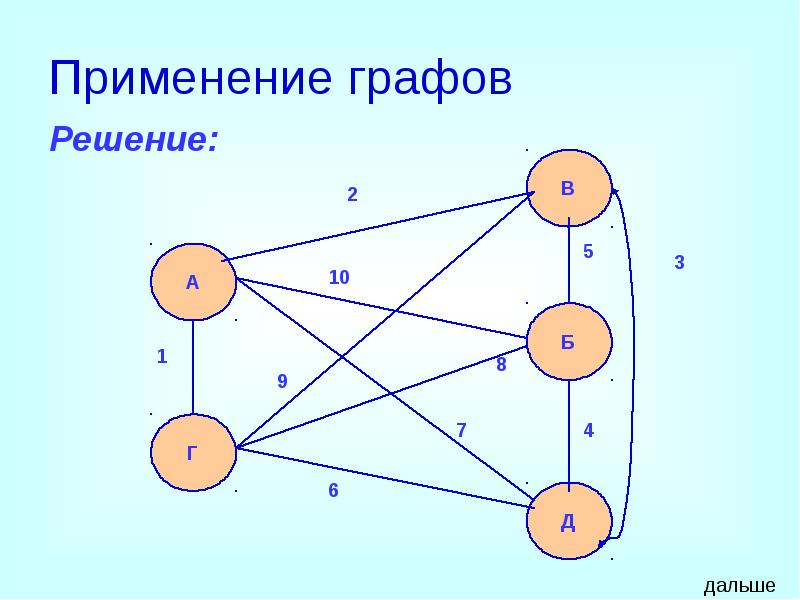
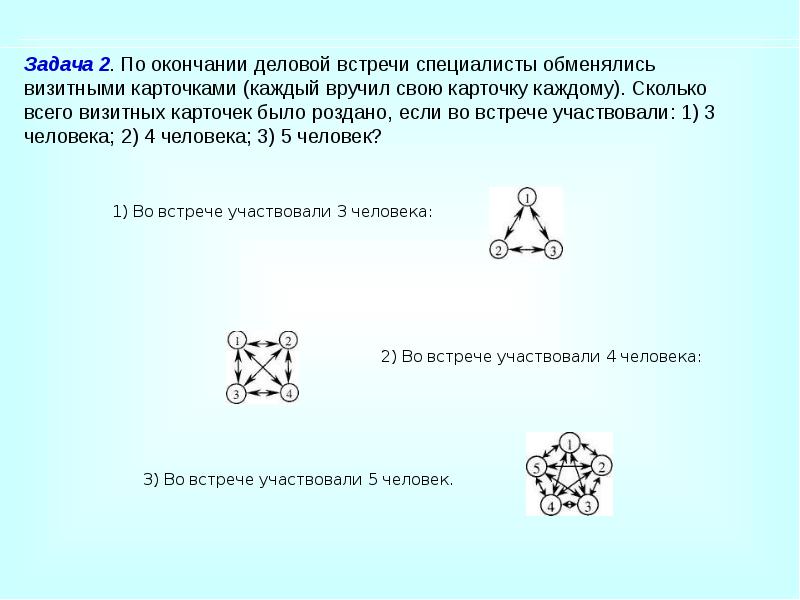
Применение графов Задача: Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?

Применение графов Решение:

Логические задачи

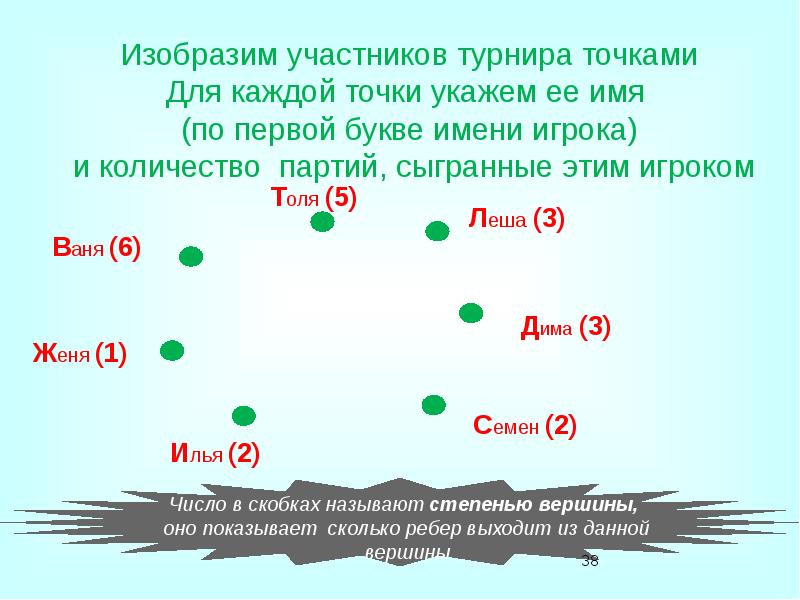
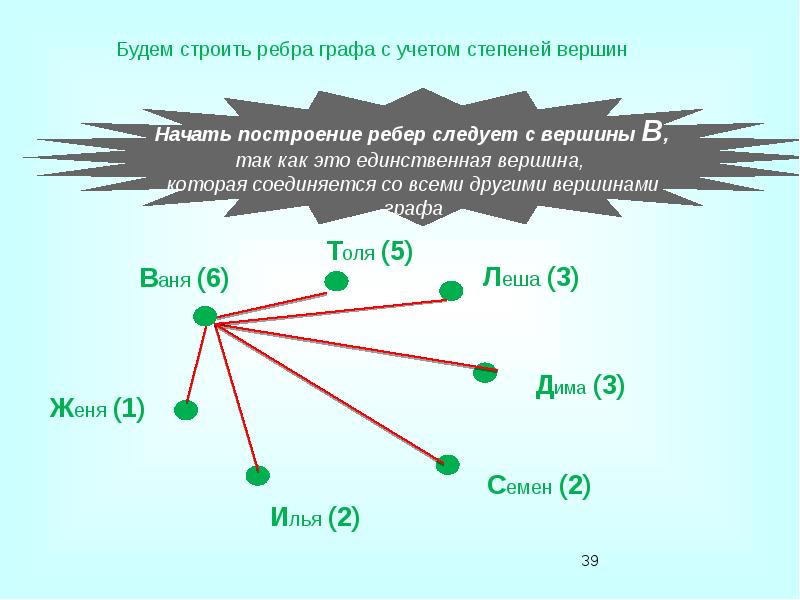
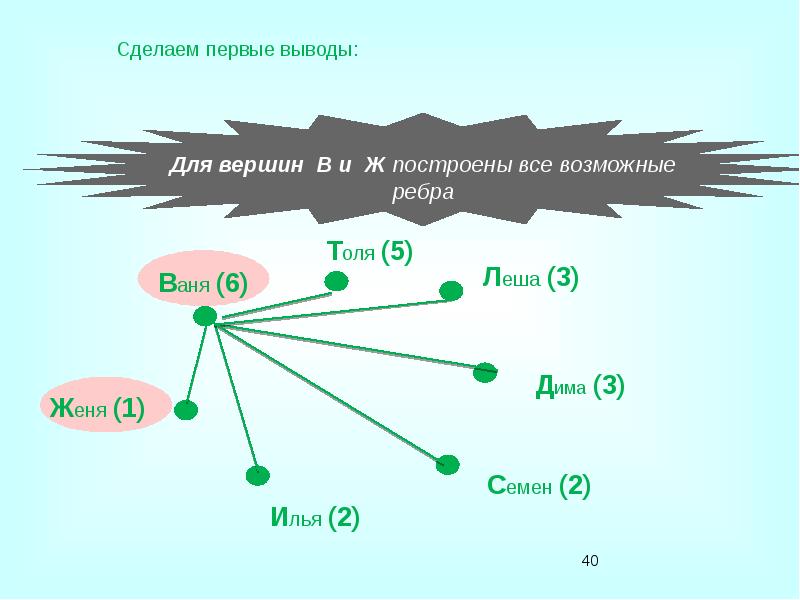
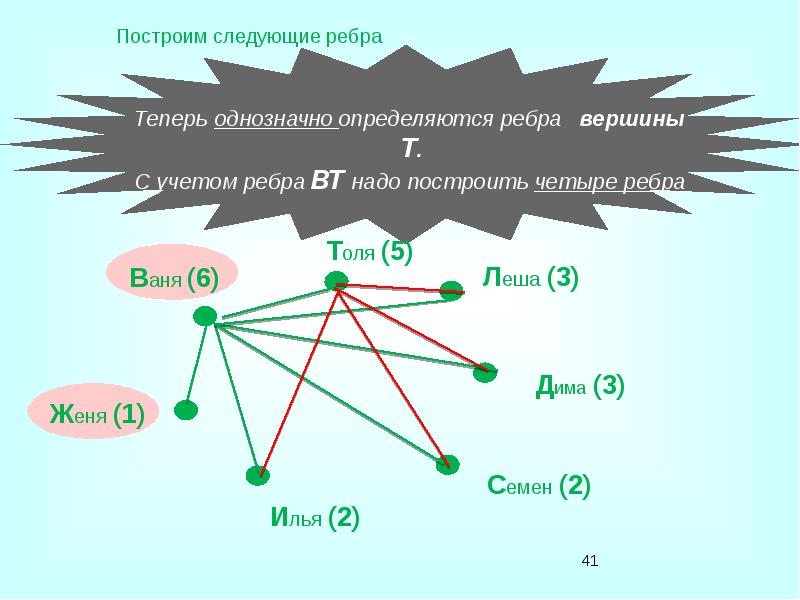
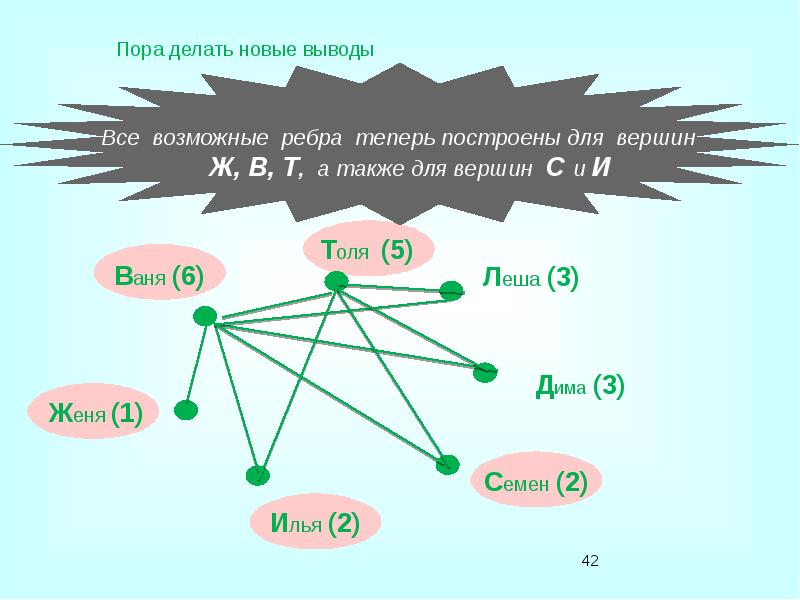
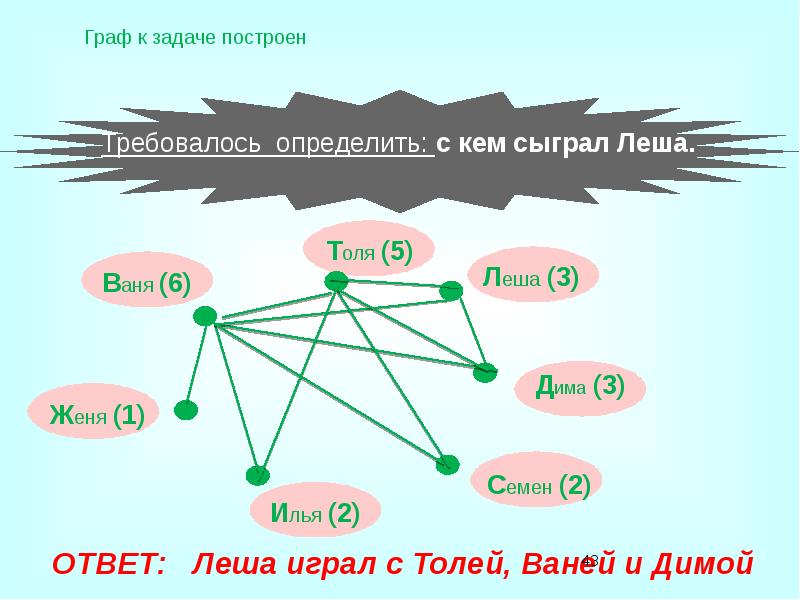
Условие задачи Известно, что в настоящий момент: Ваня сыграл шесть партий; Толя сыграл пять партий; Леша и Дима сыграли по три партии; Семен и Илья сыграли по две партии; Женя сыграл одну партию.

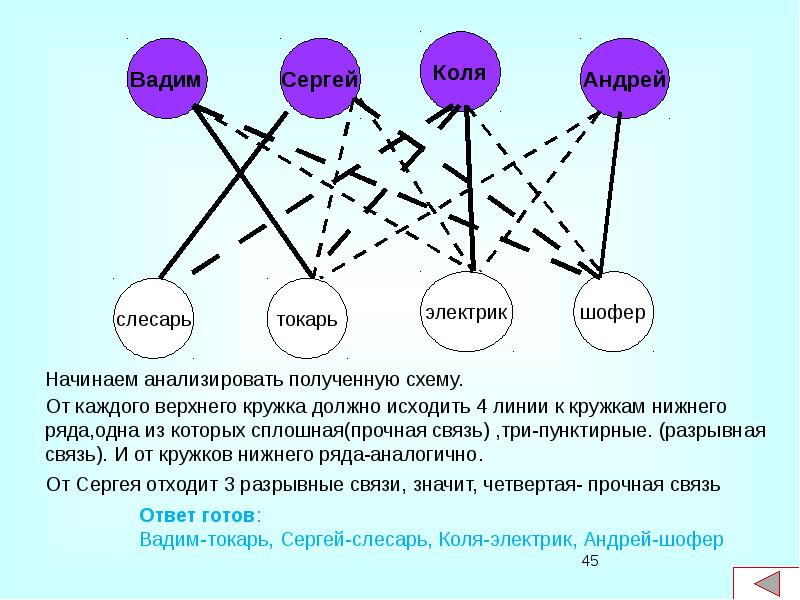
Условие задачи В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом, Электрик-младший из друзей. По вечерам Андрей и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.