Векторы в пространстве презентация
Содержание
- 2. Содержание I. Понятие вектора в пространстве II. Коллинеарные векторы III. Компланарные векторы IV. Действия с
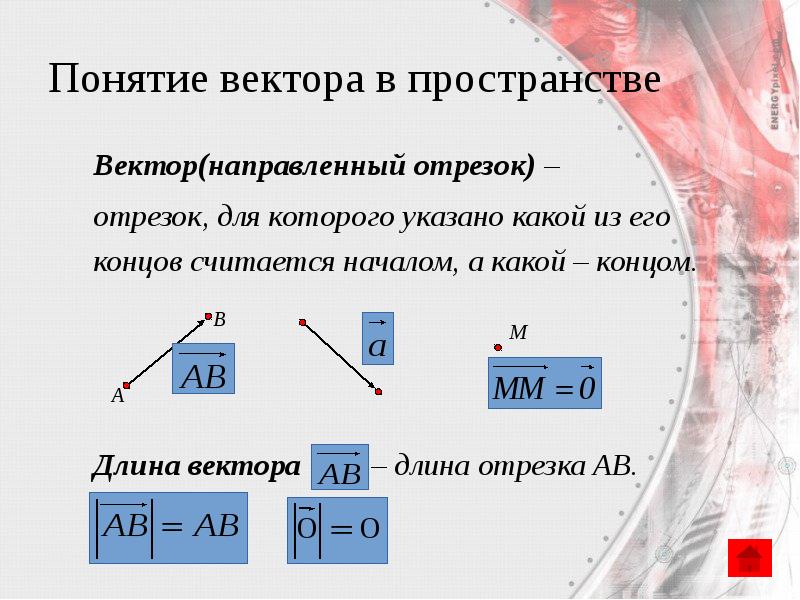
- 3. Понятие вектора в пространстве Вектор(направленный отрезок) – отрезок, для которого
- 4. Коллинеарные векторы Два ненулевых вектора называются коллинеарными, если они лежат на
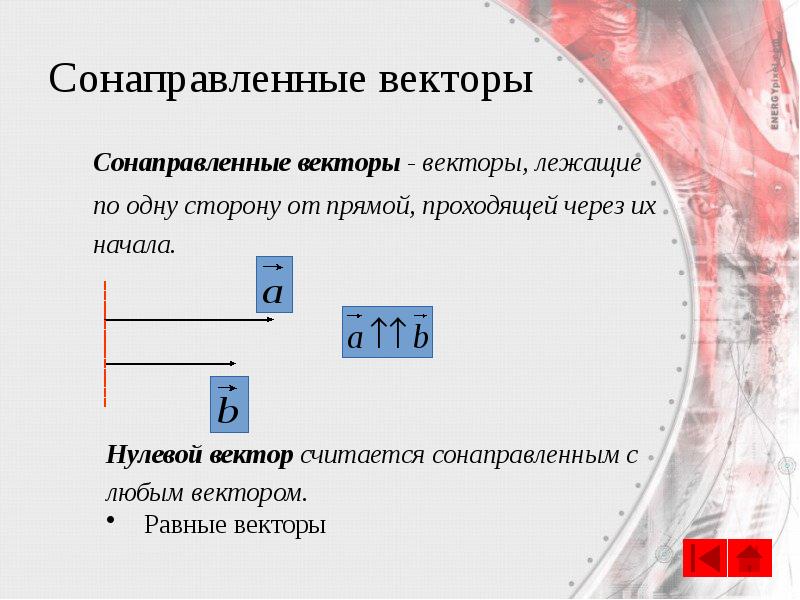
- 5. Сонаправленные векторы Сонаправленные векторы - векторы, лежащие по одну сторону
- 6. Равные векторы Равные векторы - сонаправленные векторы, длины которых равны.
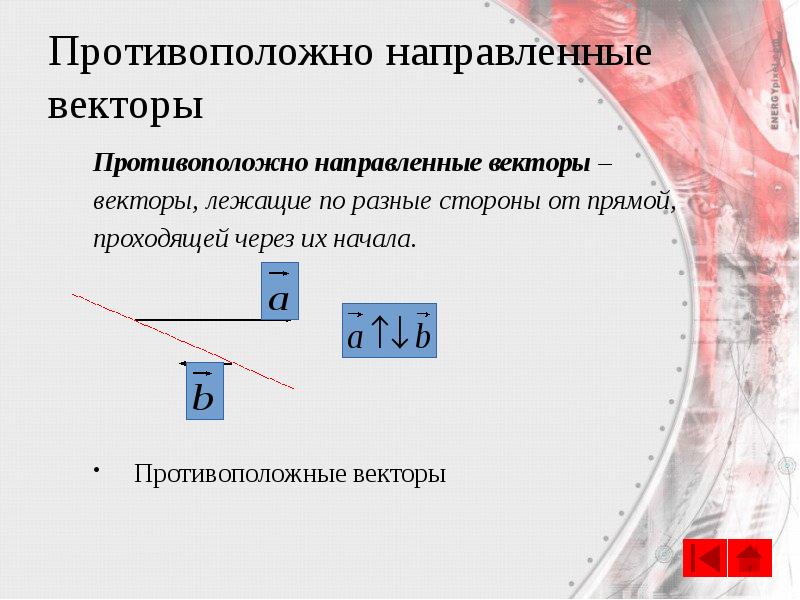
- 7. Противоположно направленные векторы Противоположно направленные векторы – векторы, лежащие по разные
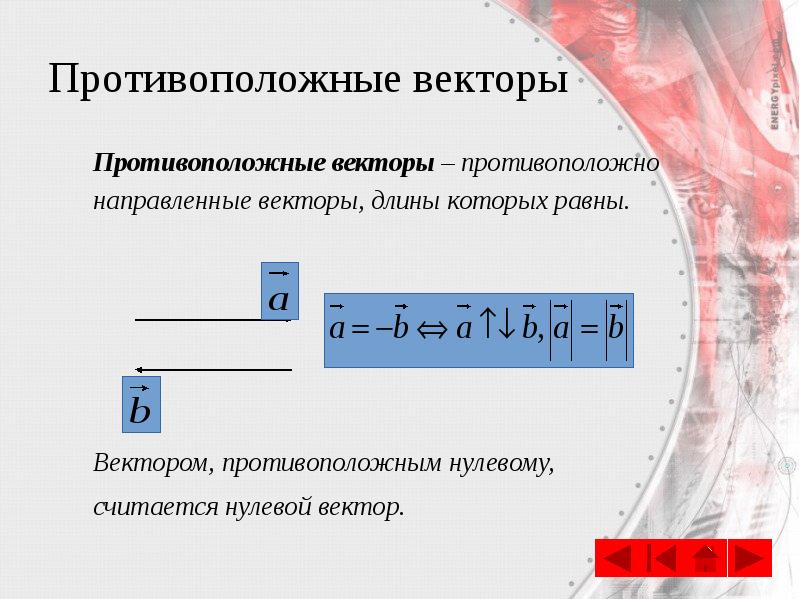
- 8. Противоположные векторы Противоположные векторы – противоположно направленные векторы, длины которых равны.
- 9. Признак коллинеарности
- 10. Определение компланарных векторов Компланарные векторы – векторы, при откладывании которых от
- 11. О компланарных векторах Любые два вектора всегда компланарны.
- 12. Признак компланарности
- 13. Свойство компланарных векторов
- 14. Действия с векторами Сложение Вычитание Умножение вектора на число Скалярное произведение
- 15. Сложение векторов Правило треугольника Правило параллелограмма Правило многоугольника Правило параллелепипеда
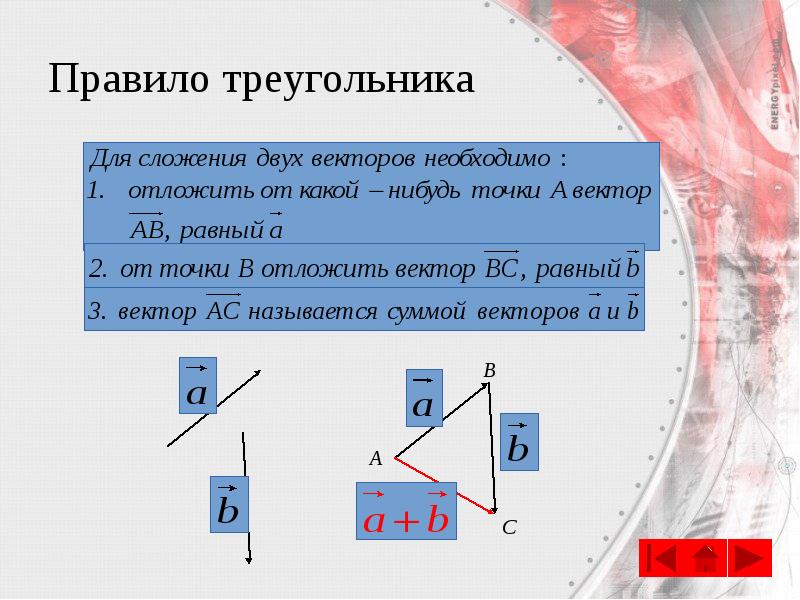
- 16. Правило треугольника
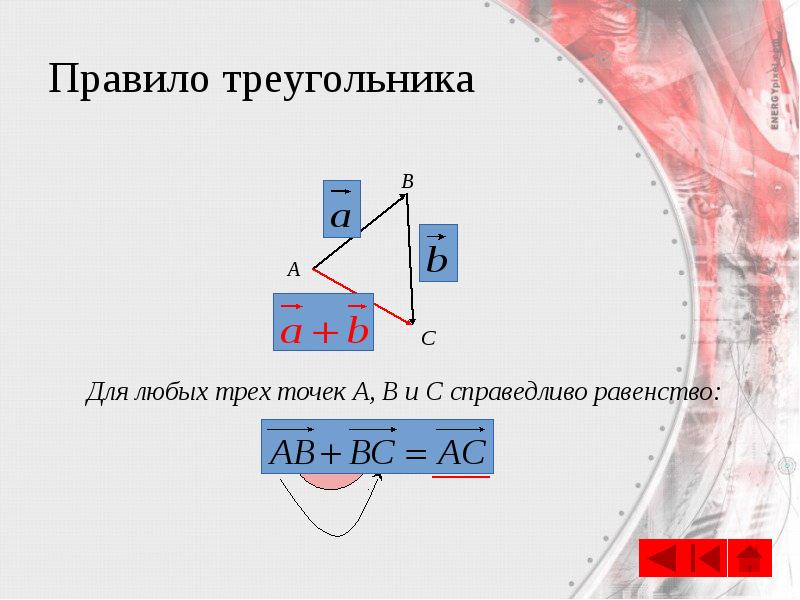
- 17. Правило треугольника
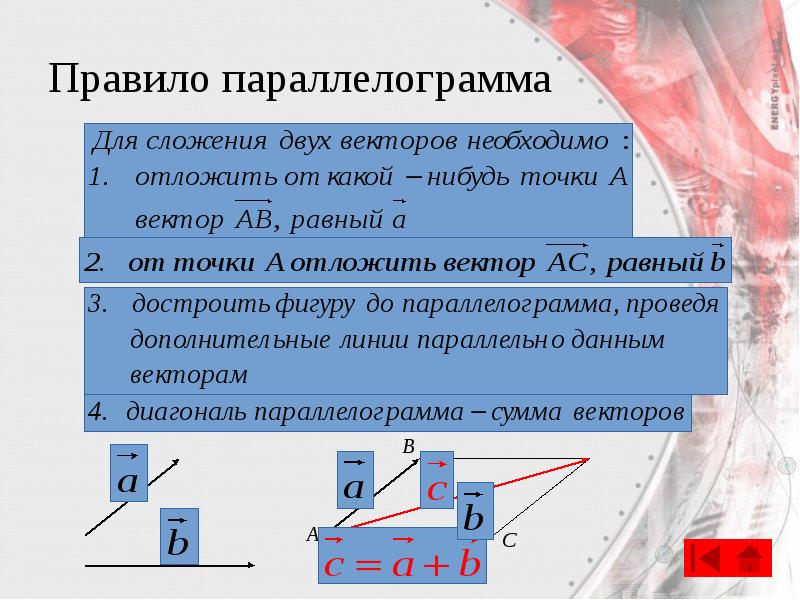
- 18. Правило параллелограмма
- 19. Свойства сложения
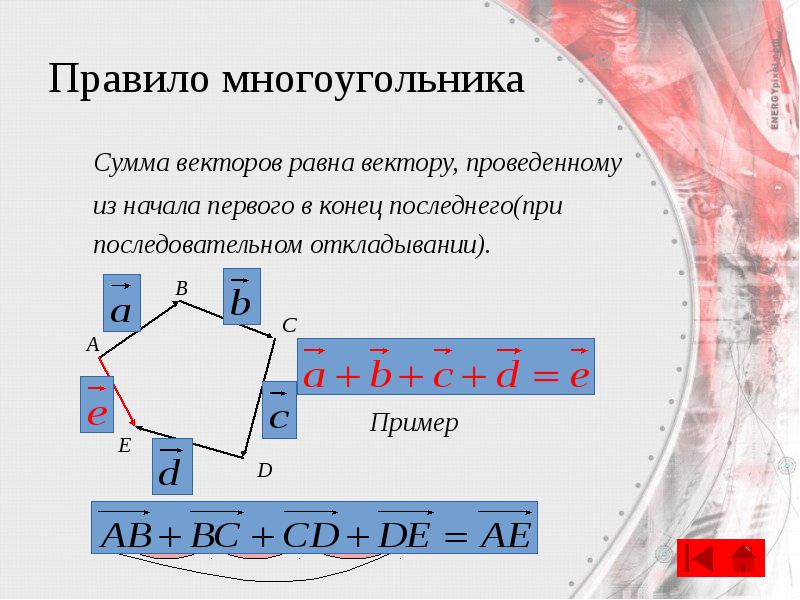
- 20. Правило многоугольника Сумма векторов равна вектору, проведенному из начала первого в
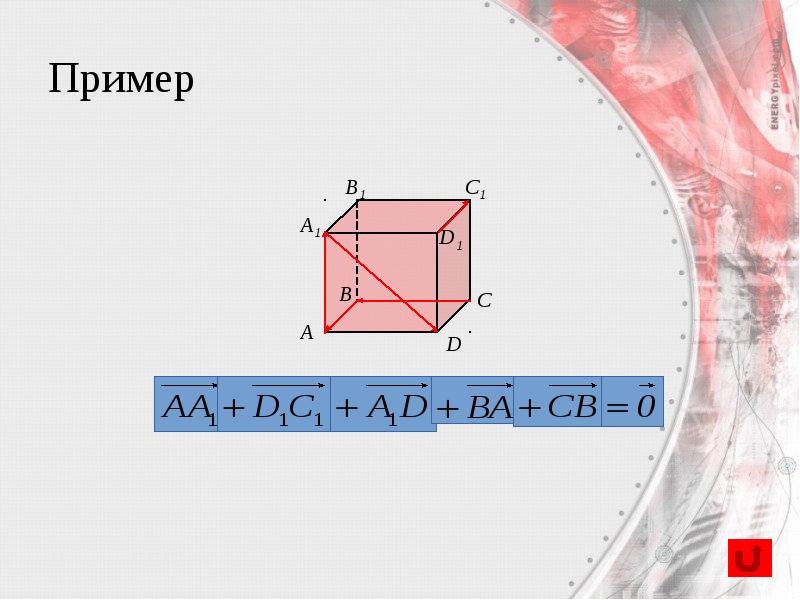
- 21. Пример
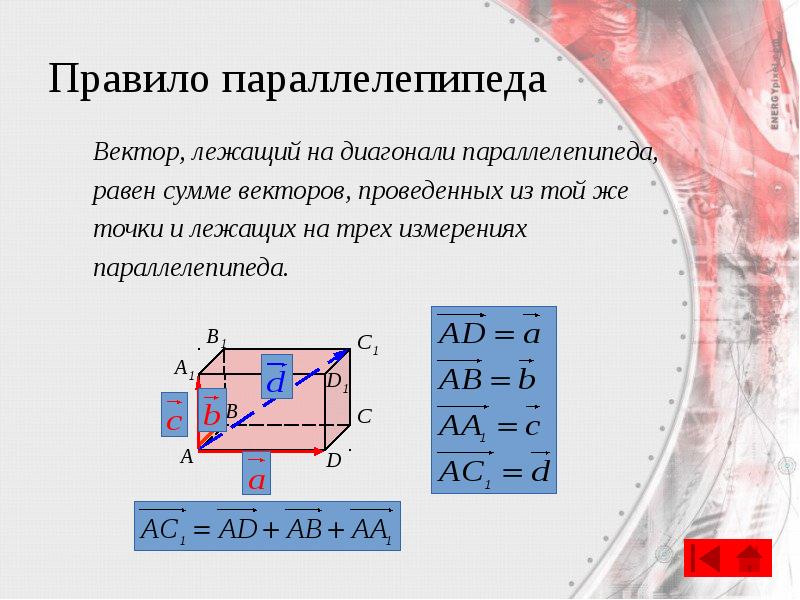
- 22. Правило параллелепипеда
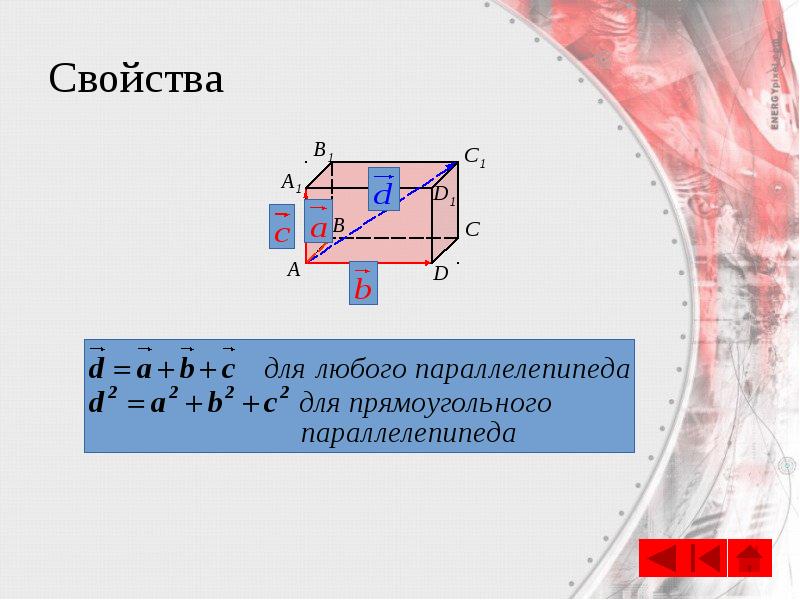
- 23. Свойства
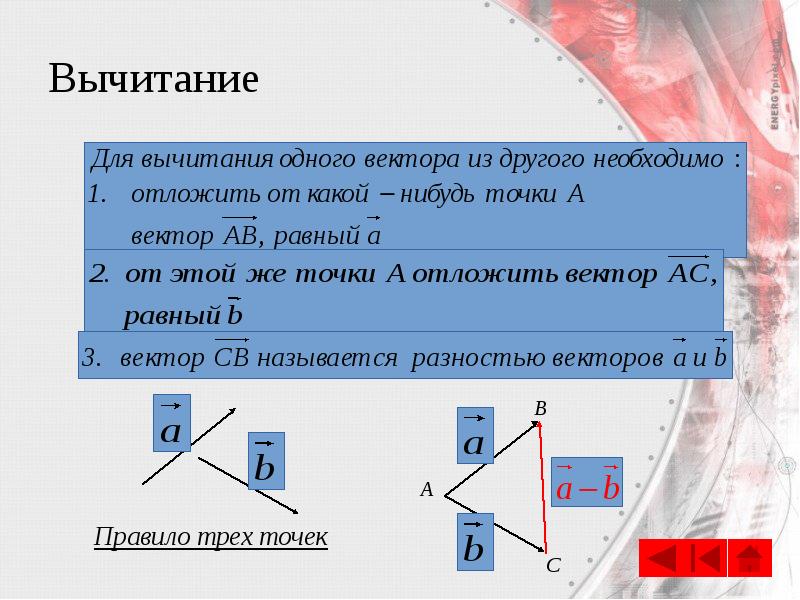
- 24. Вычитание векторов Вычитание Сложение с противоположным вектором
- 25. Вычитание Разностью векторов и называется такой вектор, сумма которого
- 26. Вычитание
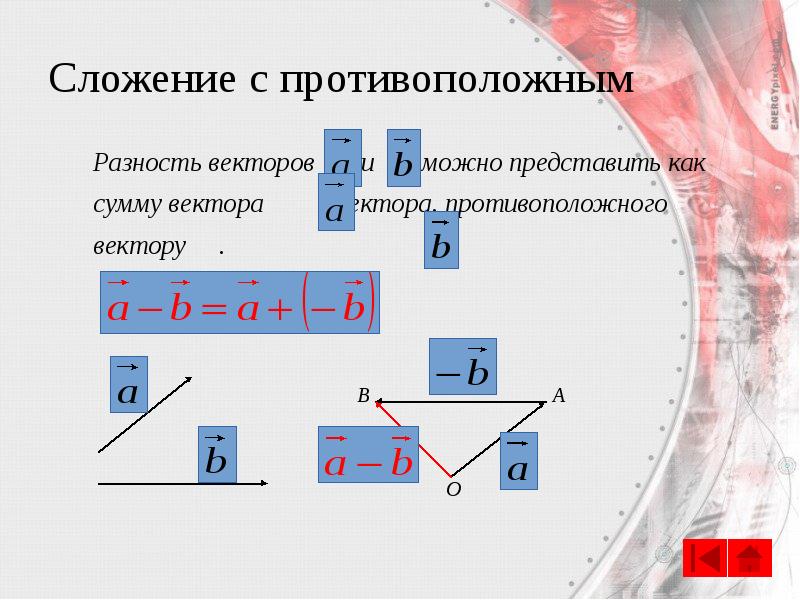
- 27. Сложение с противоположным Разность векторов и можно представить как
- 28. Умножение вектора на число
- 29. Свойства Произведением нулевого вектора на любое число считается нулевой вектор.
- 30. Свойства
- 31. Проверь себя Устные вопросы Задачи. Сложение и вычитание векторов
- 32. Устные вопросы Справедливо ли утверждение: а) любые два противоположно направленных вектора
- 33. Задача 3. Сложение и вычитание Выполните действия над векторами (рисунок): а)
- 34. Скачать презентацию




















Слайды и текст этой презентации
Похожие презентации





























