Понятие многогранника. Призма презентация
Содержание
- 2. Основные вопросы: Понятие многогранника и его элемента. Призма и её виды.
- 3. Домашнее задание Составить конспект, используя данную презентацию. Выучить основные понятия и
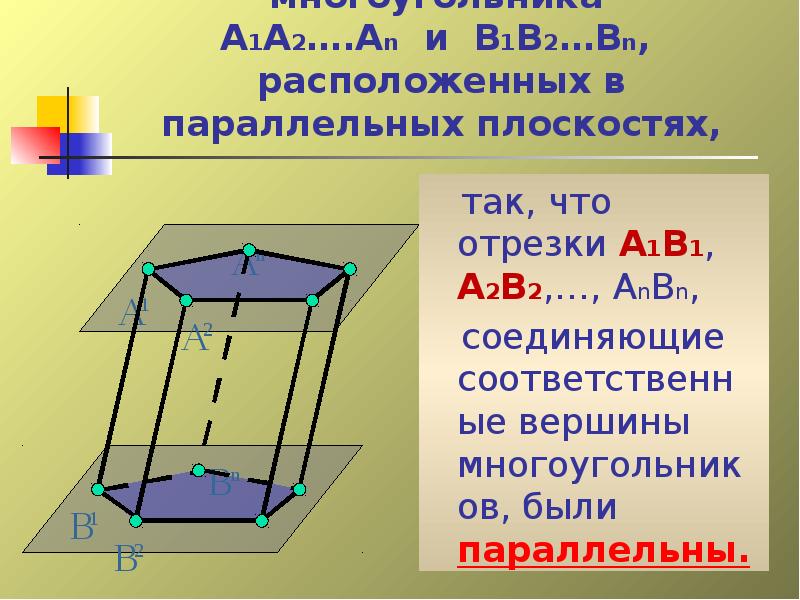
- 9. Рассмотрим два равных многоугольника А1А2….Аn и В1В2…Вn, расположенных в параллельных плоскостях,
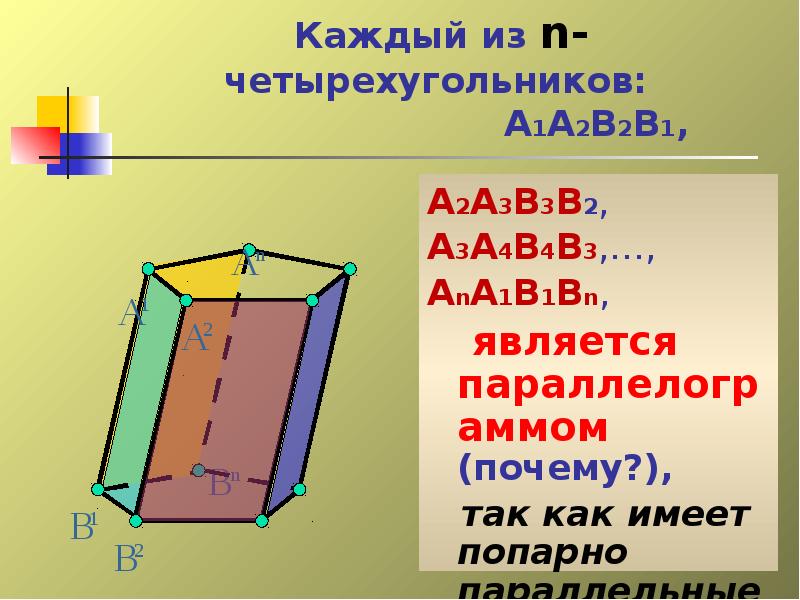
- 10. Каждый из n- четырехугольников:
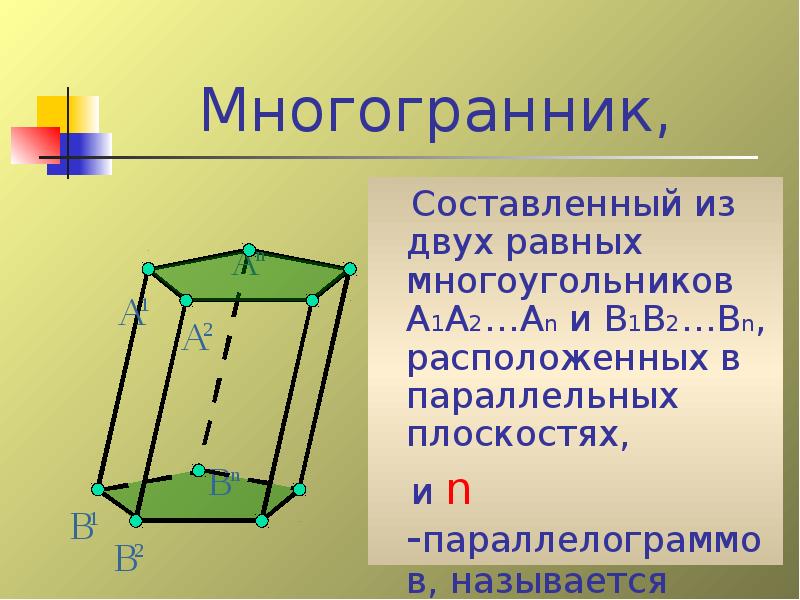
- 11. Многогранник, Составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn,
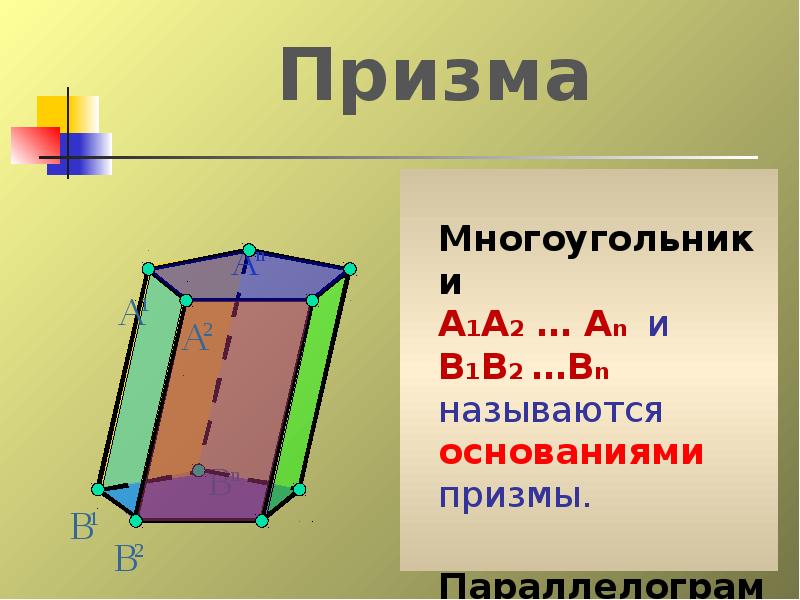
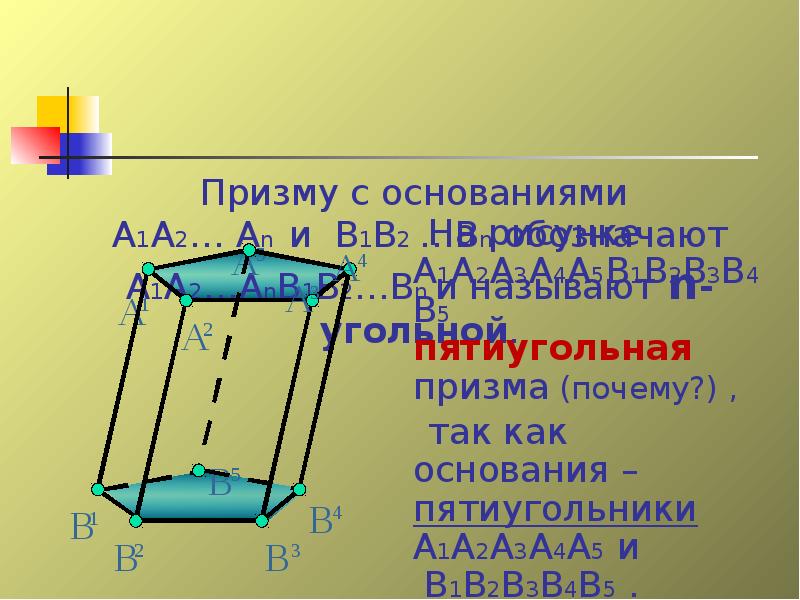
- 12. Многоугольники А1А2 … Аn и В1В2 …Вn называются основаниями призмы.
- 13. Призму с основаниями А1А2… Аn и В1В2 …Вn обозначают А1А2…АnВ1В2…Вn и
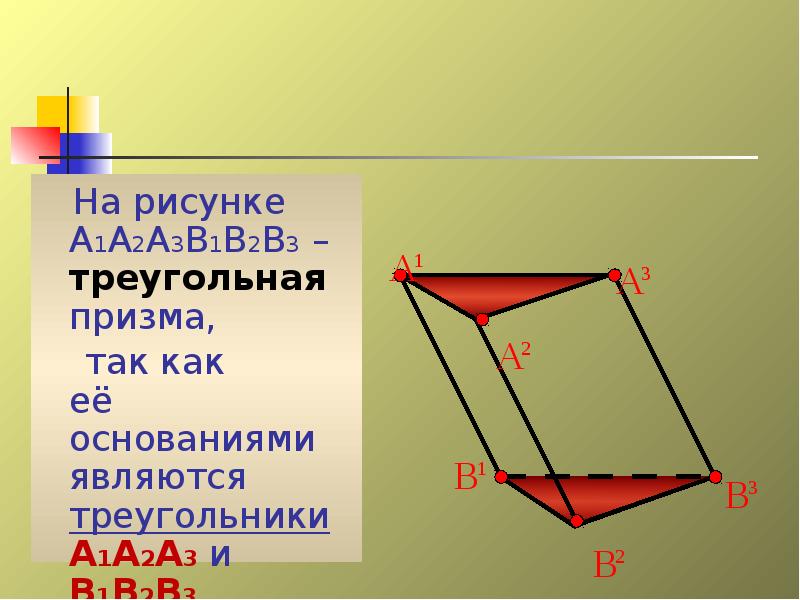
- 14. На рисунке А1А2А3В1В2В3 –треугольная призма, На рисунке А1А2А3В1В2В3 –треугольная призма,
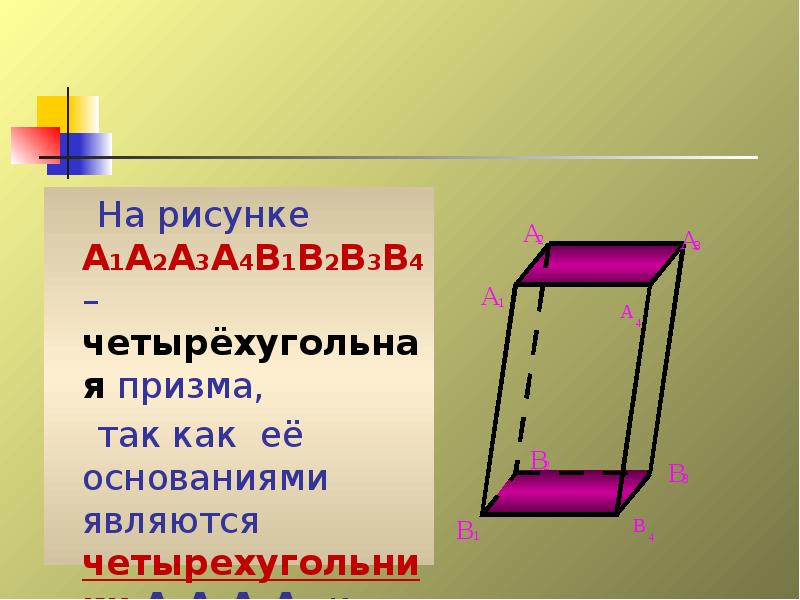
- 15. На рисунке А1А2А3А4В1В2В3В4 – четырёхугольная призма, На рисунке А1А2А3А4В1В2В3В4 –
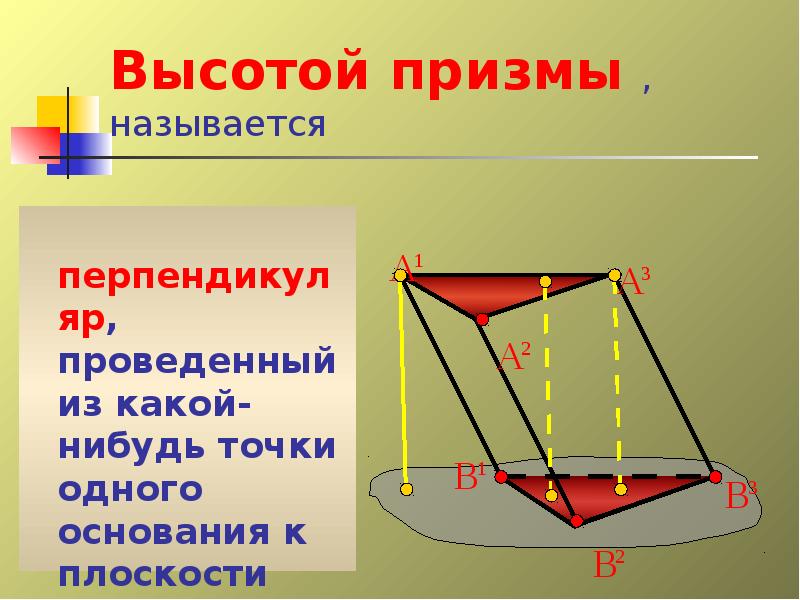
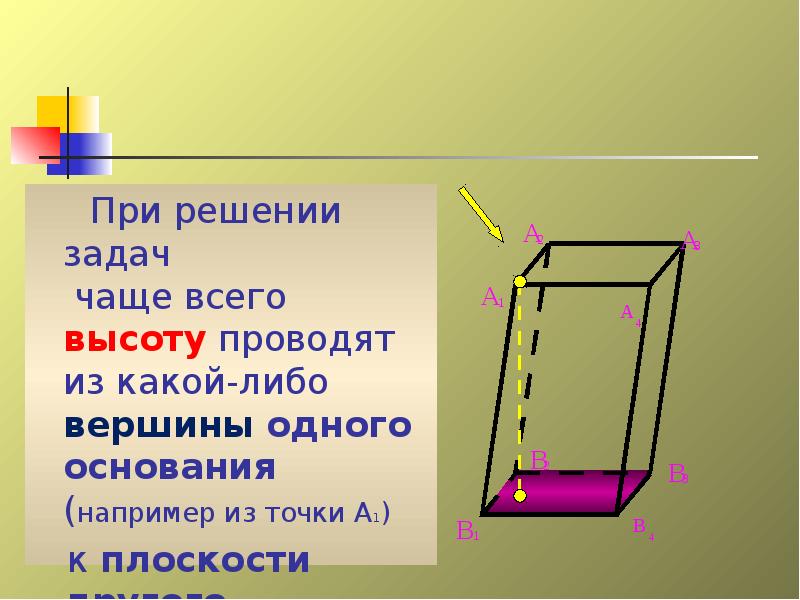
- 16. Высотой призмы , называется перпендикуляр, проведенный из какой-нибудь точки одного
- 17. При решении задач чаще всего высоту проводят из какой-либо вершины одного
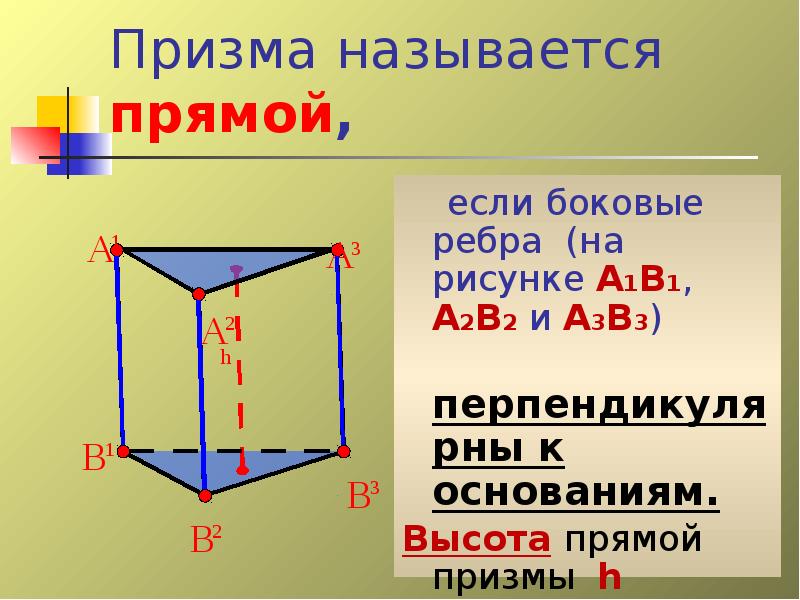
- 18. Призма называется прямой, если боковые ребра (на рисунке А1В1, А2В2
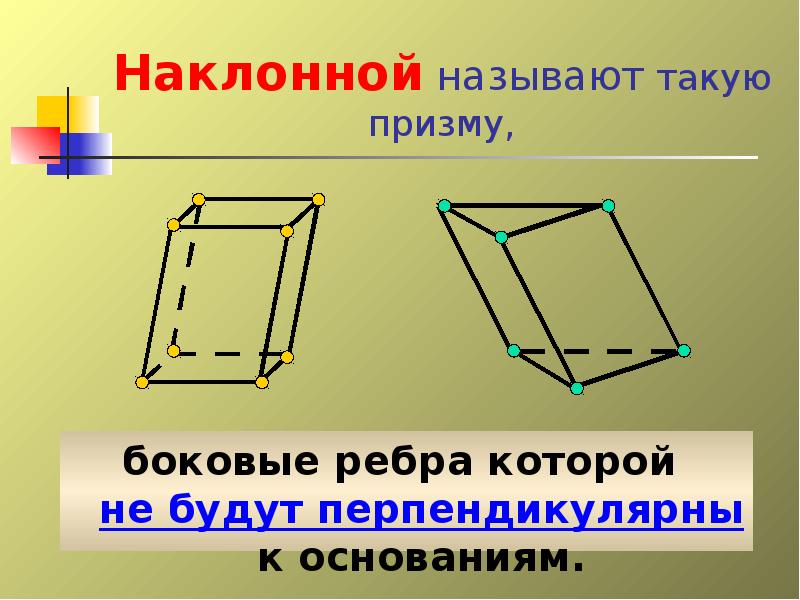
- 19. Наклонной называют такую призму, боковые ребра которой не будут перпендикулярны к
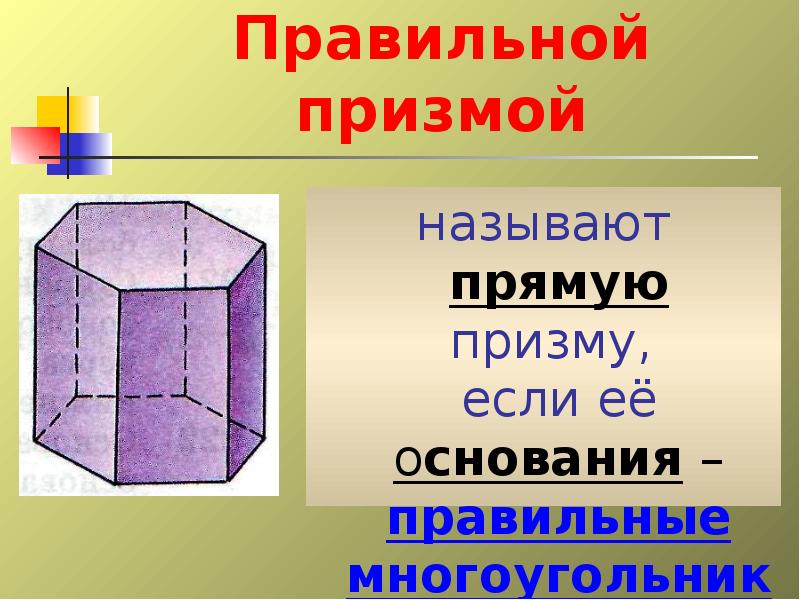
- 20. Правильной призмой называют прямую призму, если её основания – правильные многоугольники.
- 21. Свойства правильной призмы 1. Основания правильной призмы являются правильными многоугольниками. 2. Боковые
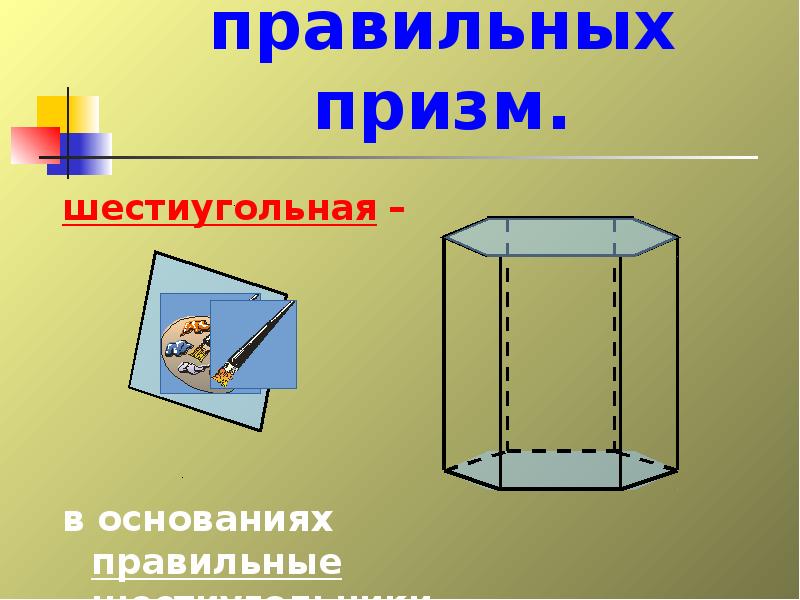
- 22. Примеры правильных призм. шестиугольная – в основаниях
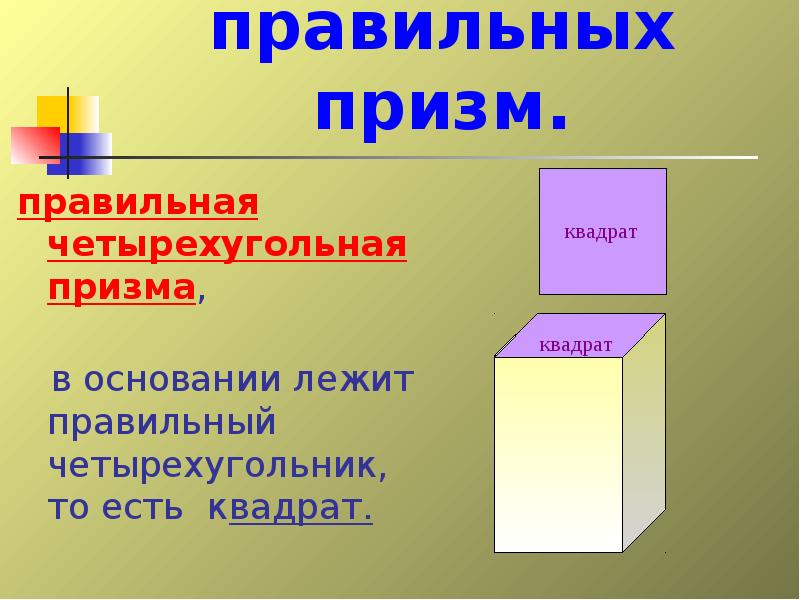
- 23. Примеры правильных призм. правильная четырехугольная призма, в основании лежит
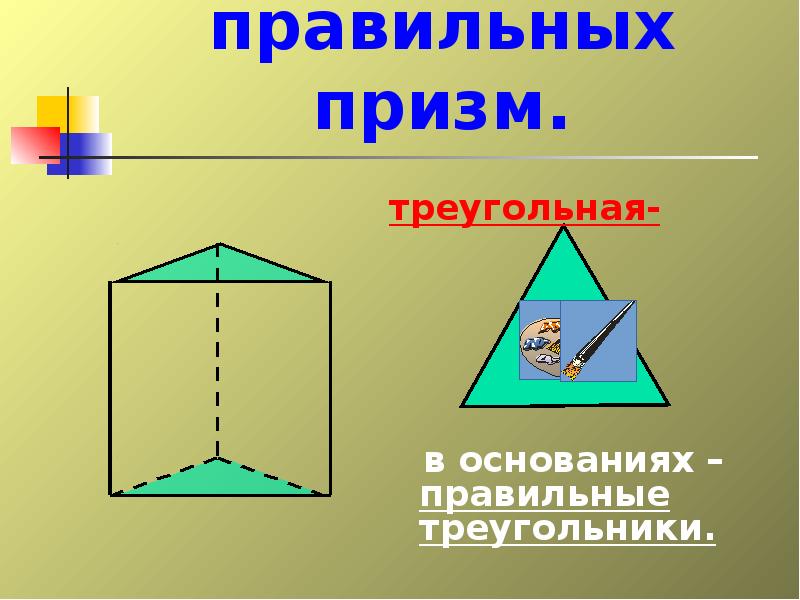
- 24. Примеры правильных призм. треугольная- в
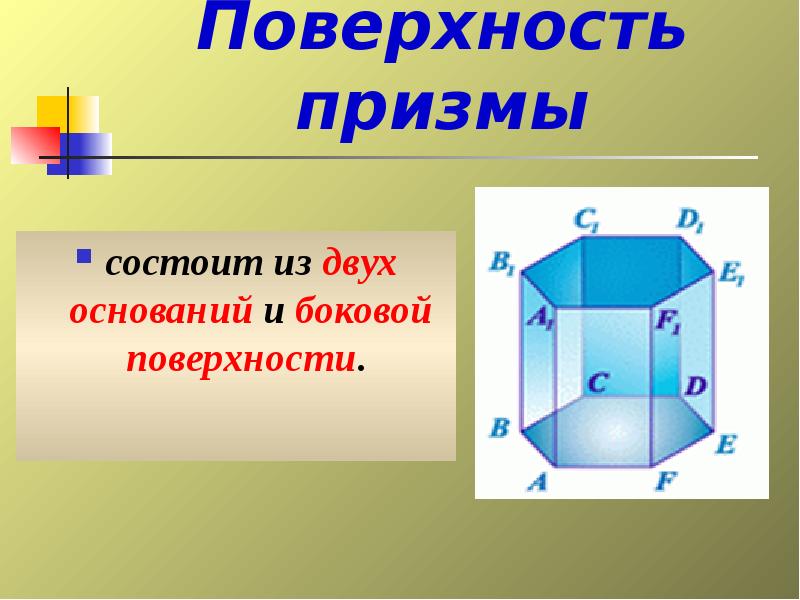
- 25. Поверхность призмы состоит из двух оснований и боковой поверхности.
- 26. Площадью боковой поверхности призмы, называется сумма площадей её боковых граней
- 27. Площадью полной поверхности призмы
- 28. Теорема о боковой поверхности прямой призмы Площадь боковой поверхности прямой призмы
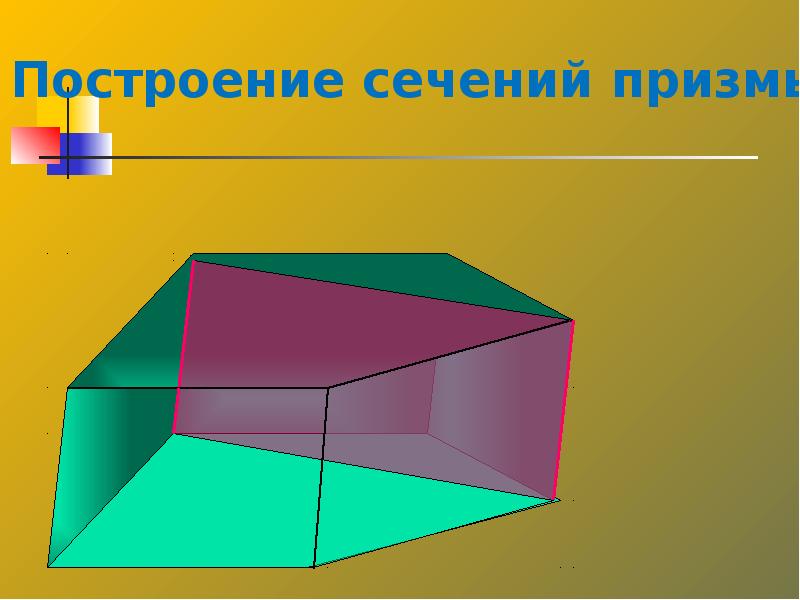
- 29. Сечения призмы Сечение призмы плоскостью, проведенной через два боковых ребра,
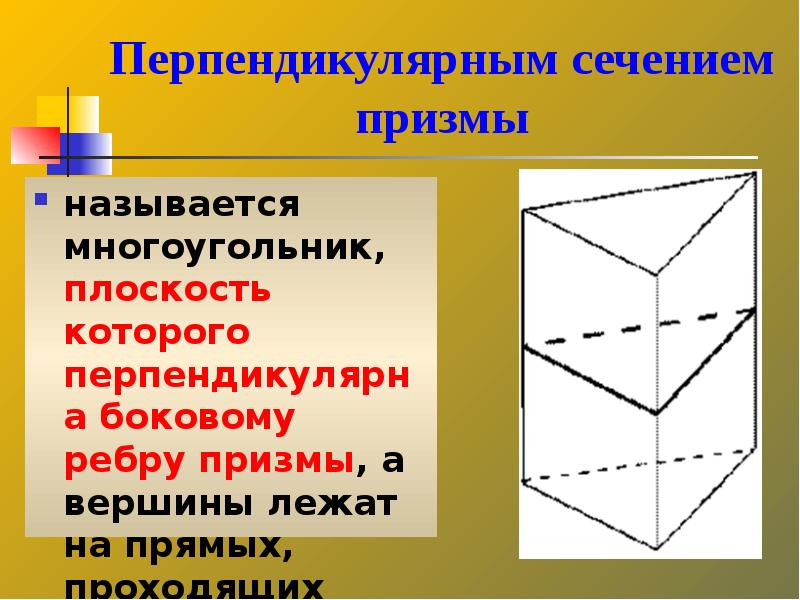
- 31. Перпендикулярным сечением призмы называется многоугольник, плоскость которого перпендикулярна боковому ребру призмы,
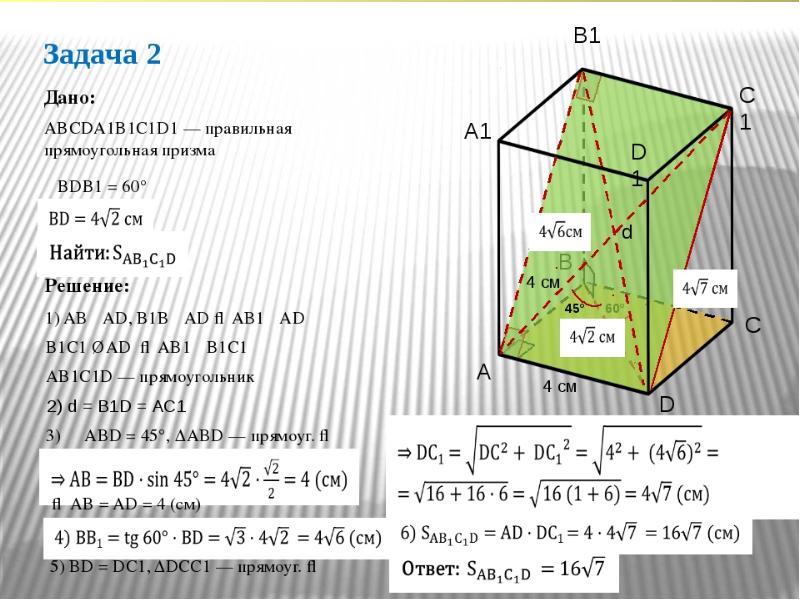
- 32. Решение задач
- 36. Задача . Основанием прямой четырехугольной призмы является ромб с диагоналями 1,6 дм
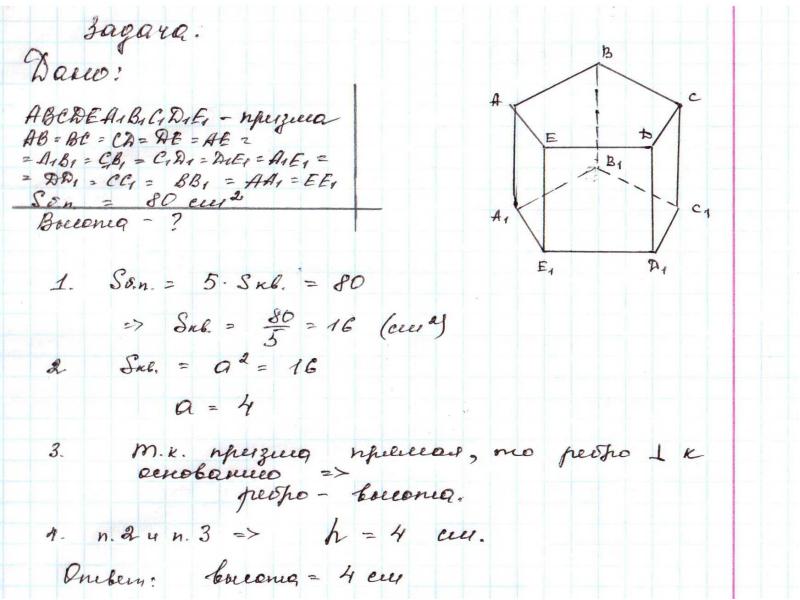
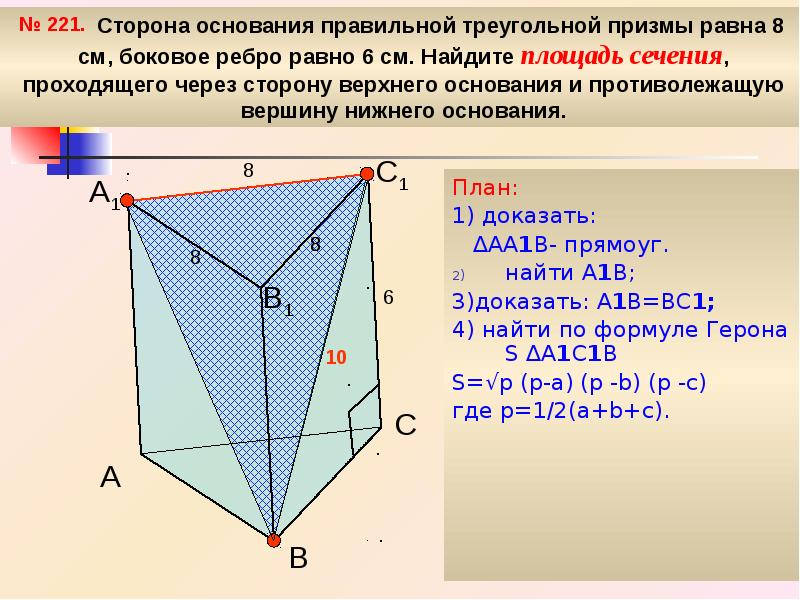
- 37. Задача . Сторона основания правильной треугольной призмы равна 8 см, боковое ребро
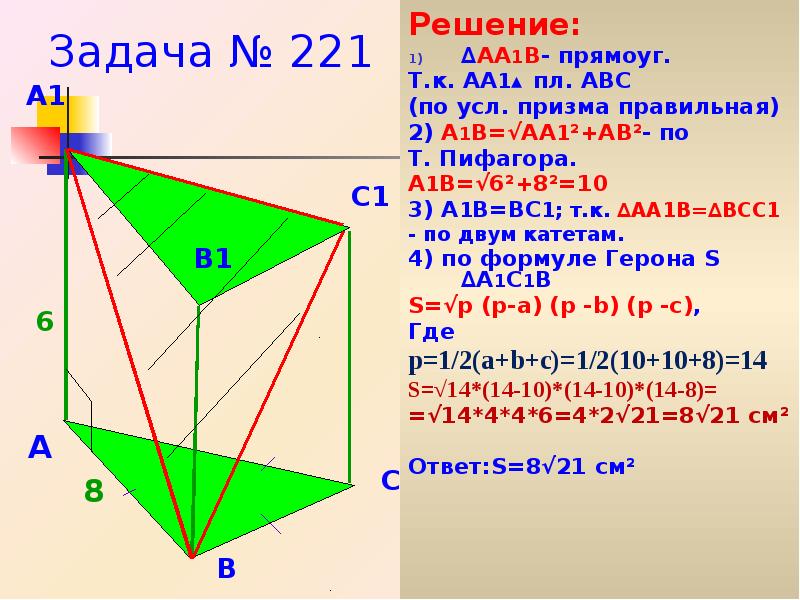
- 40. Задача № 221 Решение: ∆АА1В- прямоуг. Т.к. АА1┴ пл. АВС (по
- 41. Домашнее задание Составить конспект, используя данную презентацию. Выучить основные понятия и
- 45. Скачать презентацию



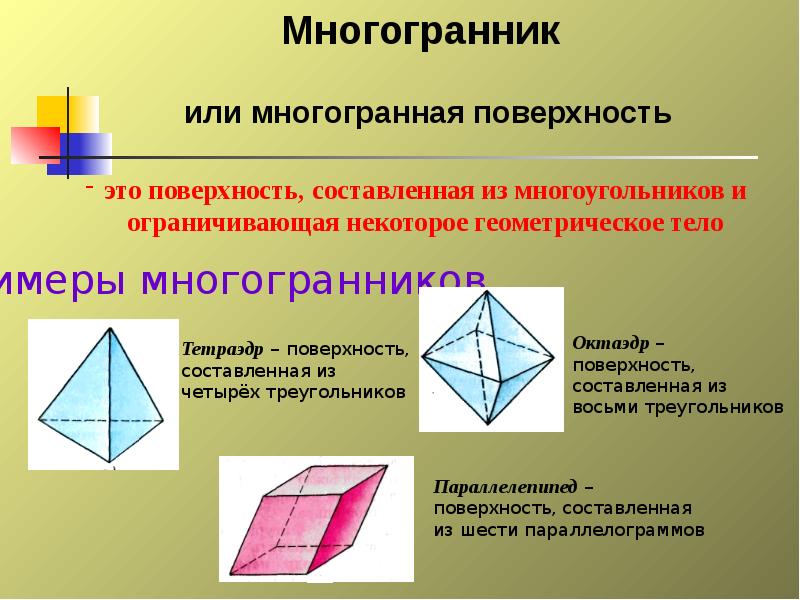
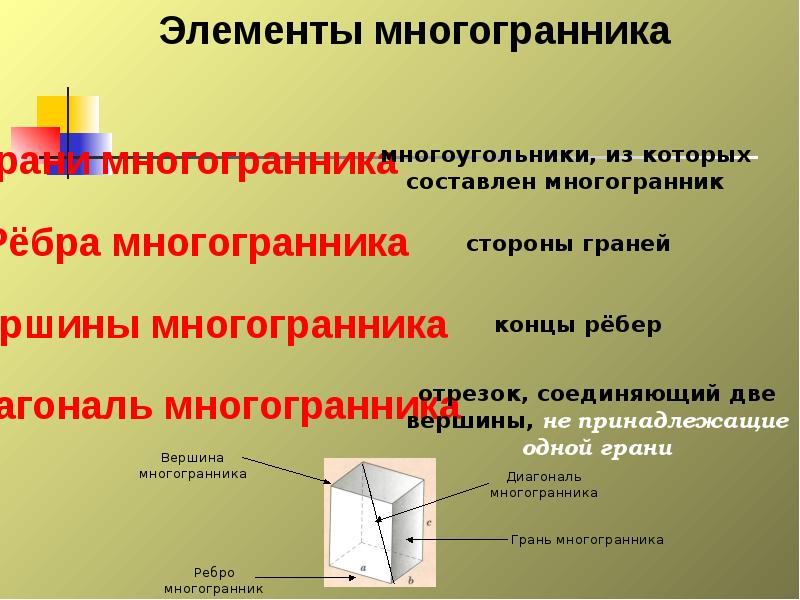
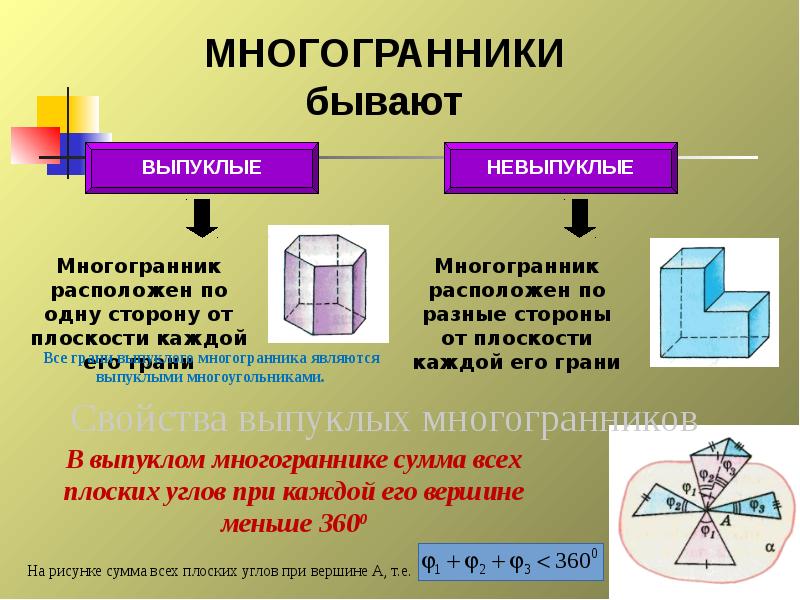

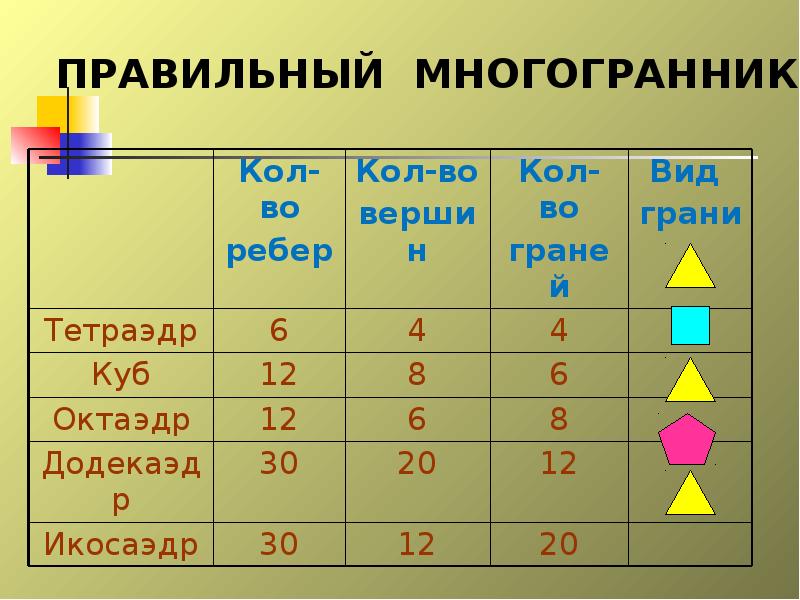











Слайды и текст этой презентации
Похожие презентации





























