Теория вероятностей презентация

Теория вероятностей Михайлова Е.А. СПБ ГБ ПОУ «КПМ»

Вероятность в природе Никто не умеет предсказывать, какой стороной («орлом» или «решкой») упадёт монета при игре в орлянку. Но опыт показывает, что если бросать монету много раз, то орлов и решек будет примерно поровну. Точно так же никто не может предсказать, сколько очков выпадет при бросании игральной кости. Но опыт показывает, что в длинной серии из N бросаний все цифры встречаются примерно поровну (каждая примерно N/6 раз).

Вероятность в природе 1. В игре бросают кубик; выигрышем считается выпадение пятёрки или шестёрки. Сколько (примерно) выигрышей будет в длинной серии из N игр?

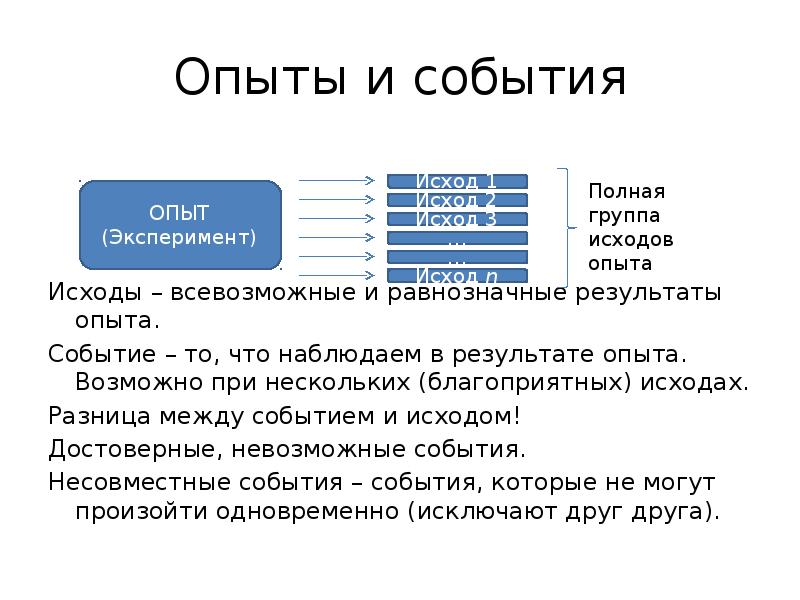
Опыты и события Исходы – всевозможные и равнозначные результаты опыта. Событие – то, что наблюдаем в результате опыта. Возможно при нескольких (благоприятных) исходах. Разница между событием и исходом! Достоверные, невозможные события. Несовместные события – события, которые не могут произойти одновременно (исключают друг друга).

Математическое (классическое) определение вероятности Определение: Вероятностью события A называется отношение числа благоприятных исходов (m) к общему числу равновозможных исходов (n).

Вероятность Вероятность – число в границах от 0 до 1 (при заполнении бланка ЕГЭ только конечная десятичная дробь) Запись: 0,6 3/5 3:5 60%

Вероятность

Вероятность

Вероятность

Вероятность

Примеры: В чемпионате по гимнастике участвуют 60 спортсменок: 17 из Венгрии, 16 из Румынии, остальные из Болгарии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Болгарии. 9773B2 Фабрика выпускает сумки. В среднем на 150 качественных сумок приходится 14 сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. 5C527A Миша, Олег, Настя и Галя бросили жребий —кому начинать игру. Найдите вероятность того, что начинать игру должна будет не Галя. B679A5

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России. D074AE Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России. D074AE Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 8 докладов, остальные распределены поровну между вторым и третьим днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции? 8C30A3 На олимпиаде по русскому языку 350 участников разместили в трёх аудиториях. В первых двух удалось разместить по 140 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. D9E4B9

Вероятность

Вероятность

Вероятность

Маша идёт на день рождения, где будут десять ребят и десять девочек (включая Машу). Они садятся за круглый стол в случайном порядке. Маша идёт на день рождения, где будут десять ребят и десять девочек (включая Машу). Они садятся за круглый стол в случайном порядке. Какова вероятность, что справа от Маши будет сидеть мальчик? что оба её соседа будут мальчики?

Вероятность

Вероятность

Двое в одной группе В классе 21 шестиклассник, среди них два друга — Митя и Петя. Класс случайным образом делят на три группы, по 7 человек в каждой. Найдите вероятность того, что Митя и Петя окажутся в разных группах. AC1A52 В классе 21 учащийся, среди них две подруги — Света и Нина. Класс случайным образом делят на семь групп, по 3 человека в каждой. Найдите вероятность того, что Света и Нина окажутся в одной группе. DFAEAD В классе 26 семиклассников, среди них два близнеца ——  Иван и Игорь. Класс случайным образом делят на две группы, по 13 человек в каждой. Найдите вероятность того, что Иван и Игорь окажутся в разных группах. 95E728

Практика Вероятность выпадения орла 0,5

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз. (D2D184) Найдите вероятность того, что орёл выпадет оба раза. (3EB10C) Найдите вероятность того, что решка выпадет ровно один раз. (40200e) Найдите вероятность того, что орёл не выпадет ни разу. (65726A)

Вероятность

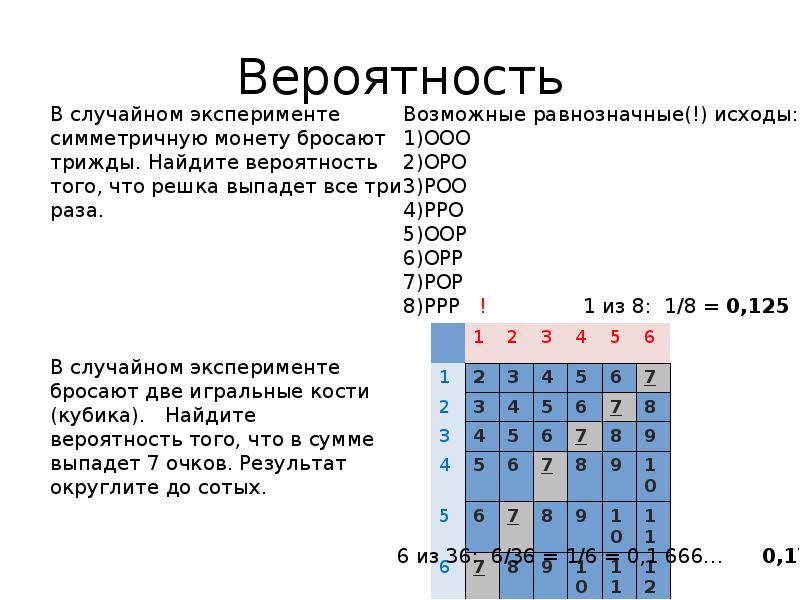
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет все три раза. B26511 В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно два раза. 08AB19

Вероятность

В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых. 3E5188 Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых. 958925 Найдите вероятность того, что в сумме выпадет 11 очков. Результат округлите до сотых. 6F772C Найдите вероятность того, что сумма выпавших очков равна 7. Результат округлите до тысячных. 4c90B4

Парадоксы теории вероятностей Парадокс игры в кости.  Правильная игральная кость при бросании с равными шансами падает на любую из граней 1,2,3,4,5 или 6. В случае бросания 2х костей сума выпавших чисел заключена между 2 и 12. Как 9, так и 10 можно получить двумя разными способами:9=3+6=4+5 и10=4+6=5+5. В задаче с тремя костями и 9 и 10 получаются шестью способами. Почему тогда 9 появляется чаще, когда бросают две кости, а 10, когда бросают три?

Одно из двух противоположных событий называется отрицанием другого Сформулируйте отрицания следующих утверждений: (а) число x больше числа y; (б) среди чисел x, y, z есть хотя бы два одинаковых; (в) все дома на правой стороне улицы имеют чётные номера; (г) все ученики класса, знающие английский язык, умеют складывать дроби; (д) Коля получил пятёрки за все контрольные; (е) любой ученик 10а класса выше по росту, чем любой ученик 8б класса. (ё) некоторый ученик 10а выше всех учеников 8б; (ж) некоторый ученик 10a выше некоторого ученика 8б; (з) все вороны чёрные; (и) на каждой странице этой книги есть хотя бы одна опечатка; (й) на каждой странице любой книги есть хотя бы одна опечатка;

Вероятность

Вероятность

Сумма вероятностей. Примеры Вероятность того, что на тестировании по математике учащийся А. верно решит больше 11 задач, равна 0,66. Вероятность того, что А. верно решит больше 10 задач, равна 0,76. Найдите вероятность того, что А. верно решит ровно 11 задач. 293735 Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°C , равна 0,89. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8°C или выше. 5B0D72 Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна 0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того, что А. верно решит ровно 6 задач.eDFD31 На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. 5e924B

Опыт состоит в одновременном бросании четырёх кубиков (красного, синего, зелёного и жёлтого). Найдите вероятность того, что Опыт состоит в одновременном бросании четырёх кубиков (красного, синего, зелёного и жёлтого). Найдите вероятность того, что (а) выпадут четыре шестёрки; (б) выпадут три шестёрки и одна пятёрка; (в) выпадут две шестёрки и две пятёрки; (г) выпадет ровно одна шестёрка; (д) выпадут четыре разные цифры; (е) не выпадет ни одной шестёрки; (ё) выпадет хотя бы одна шестёрка.

В очередь в случайном порядке становятся четыре человека А, Б, В, Г. Считая все варианты их расположения равновозможными, определите вероятность следующих событий: В очередь в случайном порядке становятся четыре человека А, Б, В, Г. Считая все варианты их расположения равновозможными, определите вероятность следующих событий: (а) А будет первым в очереди; (б) Б не будет последним в очереди; (в) А будет стоять раньше Б; (г) А будет стоять рядом с Б (до или после него); (д) А будет стоять раньше Б и раньше В; (е) А будет стоять раньше Б, а В будет стоять раньше Г.

Парадокс с подарками  Несколько человек решили сделать друг другу подарки следующим образом. Каждый приносит подарок. Подарки перемешиваются и случайно распределяются среди участников. Этот справедливый способ применяется часто, так как считается, что вероятность получения кем-то собственного подарка очень мала. Парадоксально, но вероятность по крайней мере одного совпадения намного больше вероятности того, что совпадения нет (кроме тривиального случая из двух человек). Почему так? 

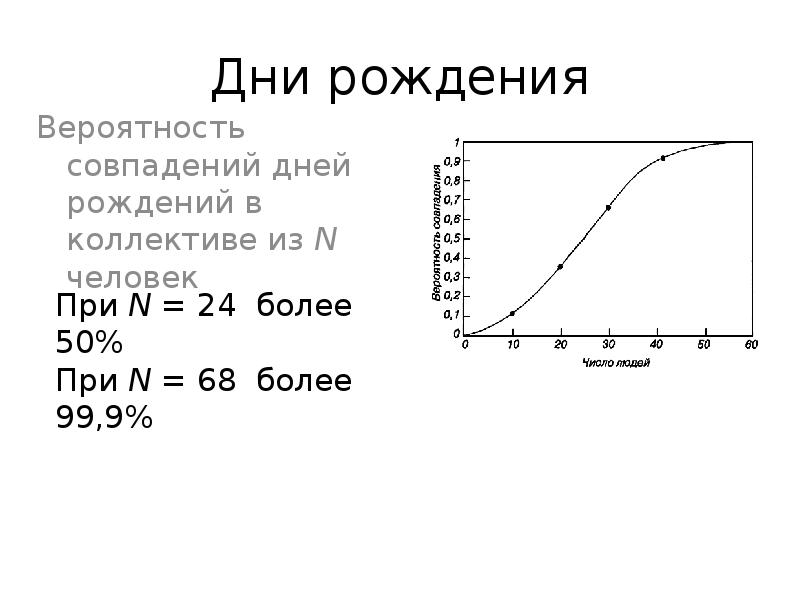
Дни рождения Вероятность совпадений дней рождений в коллективе из N человек

Произведение вероятностей. Примеры Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. 905979 Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей —  1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3. 21DD4A

Парадокс лотереи (типа спортлото)  Большинство участников лотерей (в которых выигрыш распределяется между всеми победителями как в спортлото) обычно не ставят на "слишком симметричные" комбинации, хотя все комбинации равновозможны. Причина этого проста. Игроки по опыту знают, что, как правило, выигрывают не симметричные комбинации. В действительности выгоднее ставить на наиболее симметричные комбинации именно потому, что…. Почему?

Парадокс смертности. Эдмунд Галлей (открывший известную комету) в 1693 году составил таблицу смертности, положившую начало математической теории страхования жизни. По этой таблице средняя продолжительность жизни равна 26 годам, и вместе с тем с равными шансами можно умереть до 8 лет и прожить больше 8 лет. Как это увязать?

Геометрическая вероятность. Пример Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1. 26190D

Источники Г. Секей. "Парадоксы в теории вероятностей и математической статистике" М., Мир 1990. А. Шень. «Вероятность: примеры и задачи» М., МЦНМО 2008. http://alexlarin.net/kvm4.html