Перпендикулярные прямые в пространстве» презентация

«Перпендикулярные прямые в пространстве» «Параллельные прямые, перпендикулярные к плоскости». «Перпендикулярность прямой и плоскости»

Цели урока: Ввести понятие перпендикулярных прямых в пространстве; Доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой; Дать определение перпендикулярности прямой и плоскости; Доказать теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярности к плоскости.

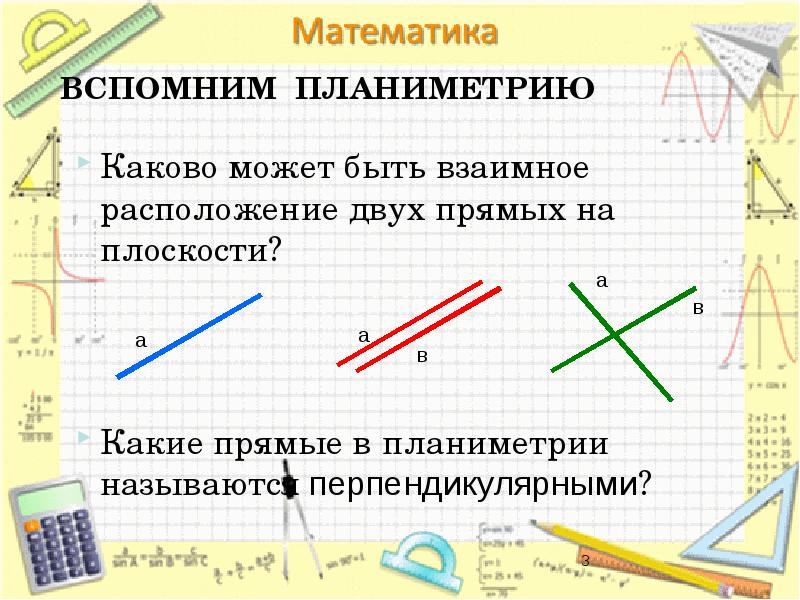
ВСПОМНИМ ПЛАНИМЕТРИЮ Каково может быть взаимное расположение двух прямых на плоскости? Какие прямые в планиметрии называются перпендикулярными?

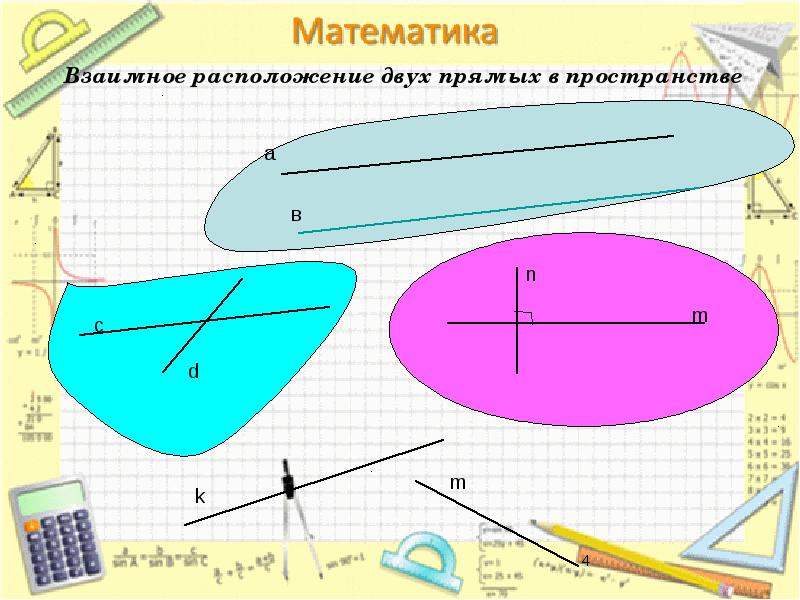
Взаимное расположение двух прямых в пространстве

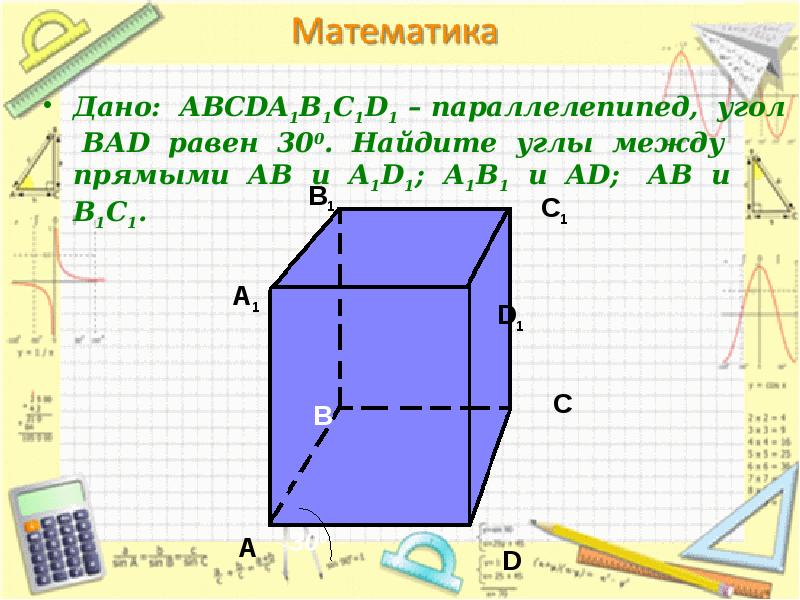
Дано: АВСDA1B1C1D1 – параллелепипед, угол ВАD равен 300. Найдите углы между прямыми АВ и А1D1; А1В1 и АD; АВ и В1С1.

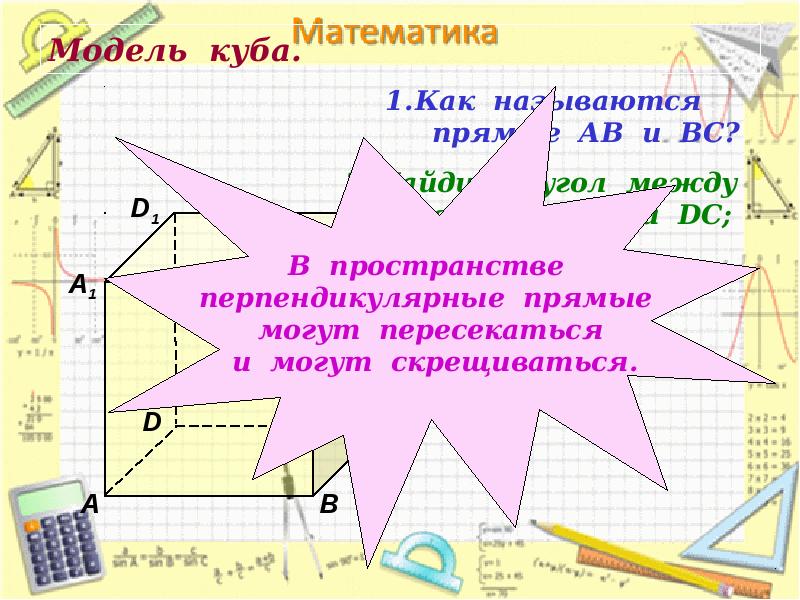
Модель куба.

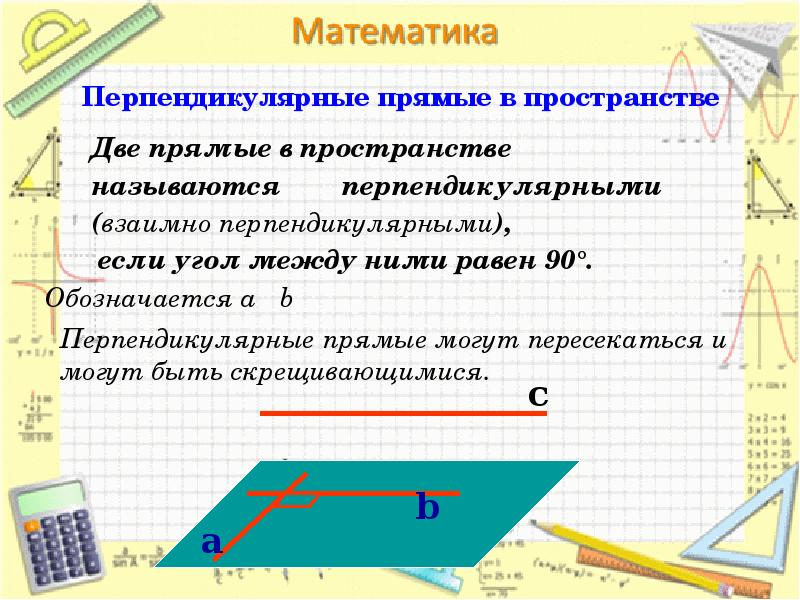
Перпендикулярные прямые в пространстве Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°. Обозначается a ┴ b Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

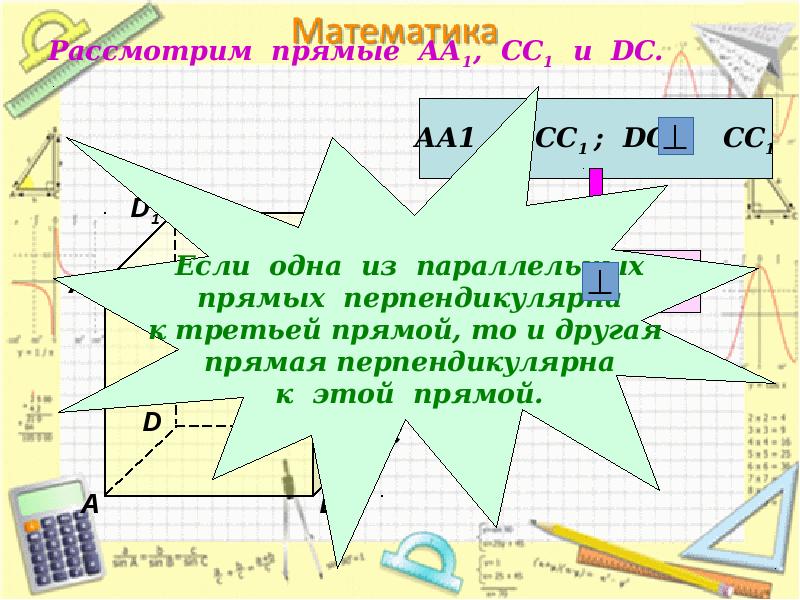
Рассмотрим прямые АА1, СС1 и DC.

Свойства : 1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна другой прямой. (a ⊥ α b и a II b => b ⊥ α) 2. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны. (a ⊥ α и b ⊥ α => a II b) 3. Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости. (α II β и a ⊥ α => a ⊥ β)

Свойства : 4. Если две различные плоскости перпендикулярны одной и той же прямой, то эти плоскости параллельны. (a ⊥ α и a ⊥ β => a II β) 5. Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости, и притом только одну. 6. Через любую точку прямой можно провести плоскость, перпендикулярную ей и притом только одну.

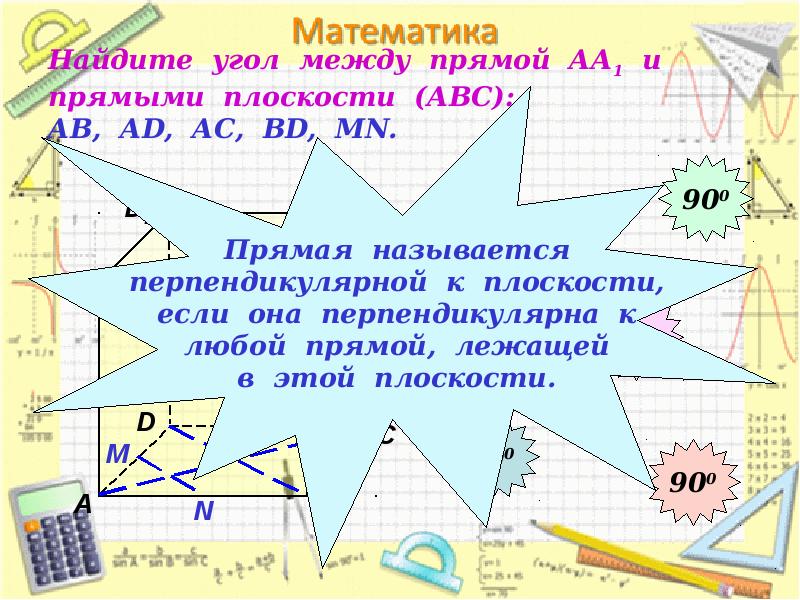
Найдите угол между прямой АА1 и прямыми плоскости (АВС): АВ, АD, АС, ВD, МN.

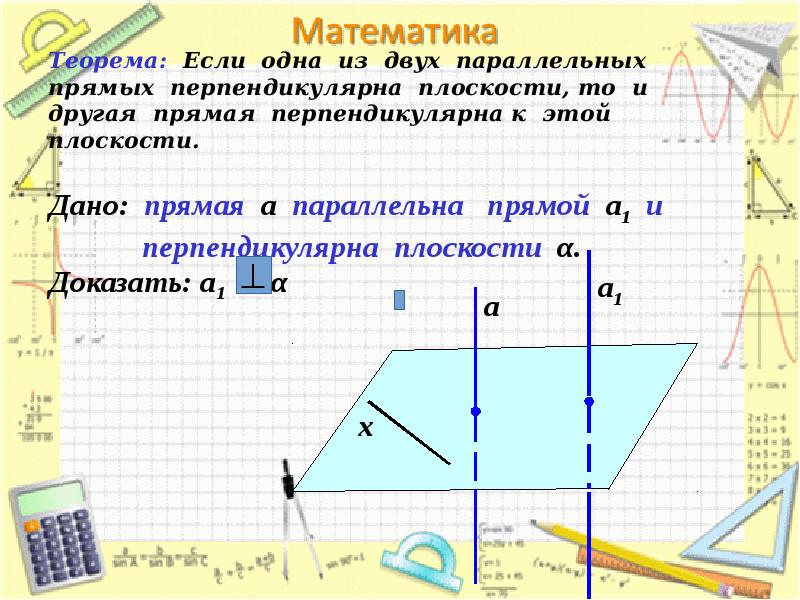
Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости. Дано: прямая а параллельна прямой а1 и перпендикулярна плоскости α. Доказать: а1 α

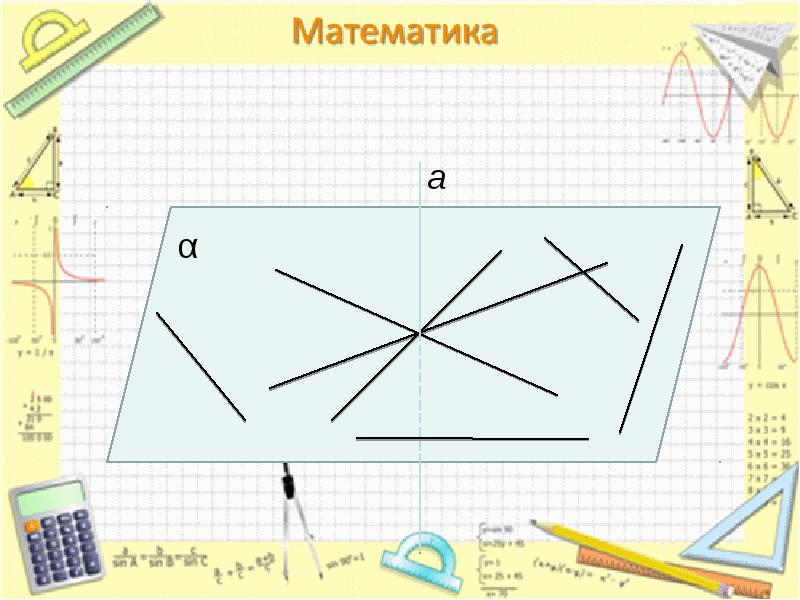
Проведем прямую х в плоскости . Так как а, то ах. По лемме о перпендикулярности двух параллельных прямых к третьей а х. Т.о., прямая а1 перпендикулярна к любой прямой, лежащей в плоскости , т.е. а .

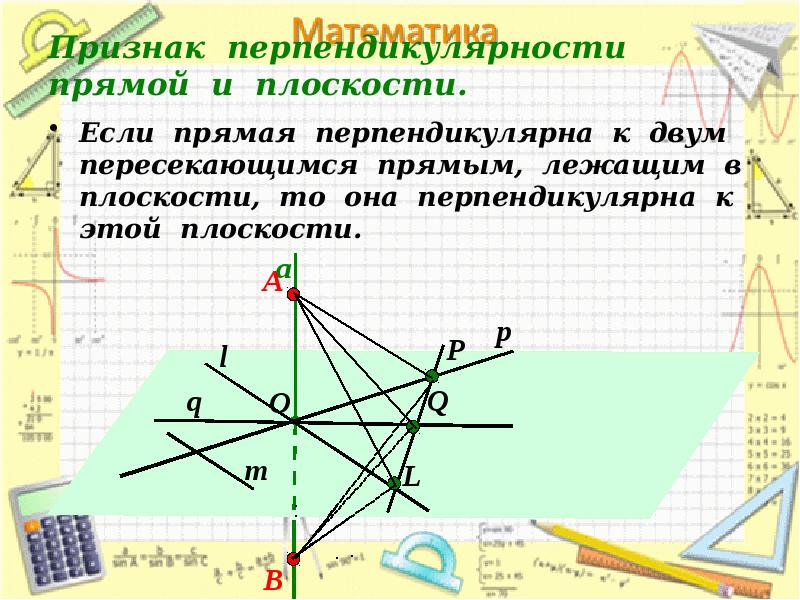
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

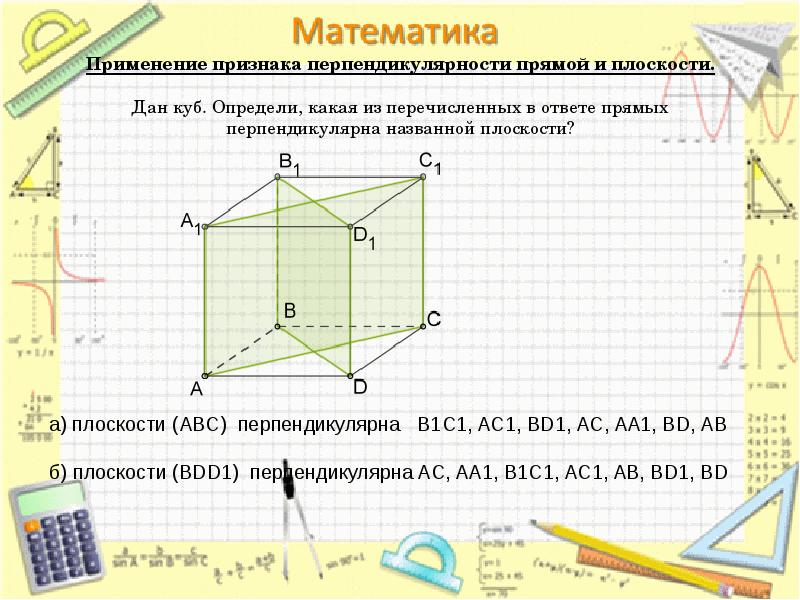
Применение признака перпендикулярности прямой и плоскости.   Дан куб. Определи, какая из перечисленных в ответе прямых перпендикулярна названной плоскости?

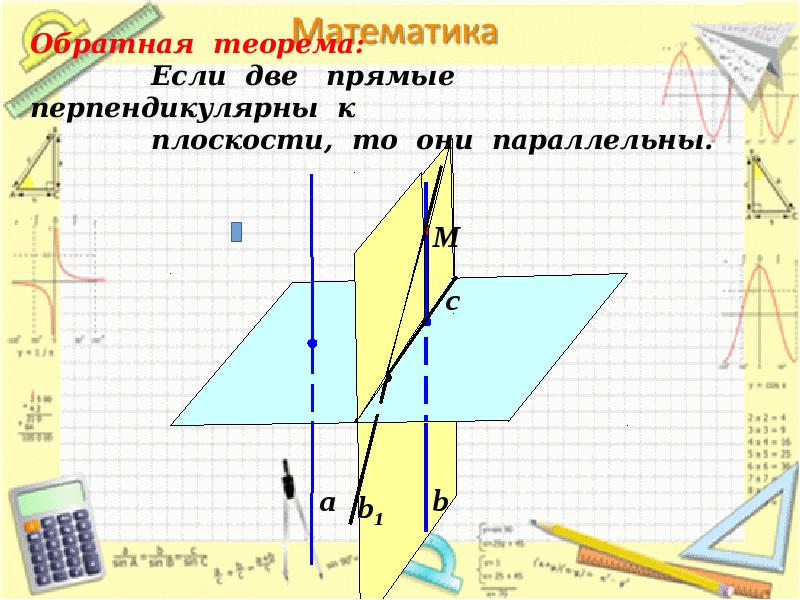
Две прямые, перпендикулярные одной плоскости.  

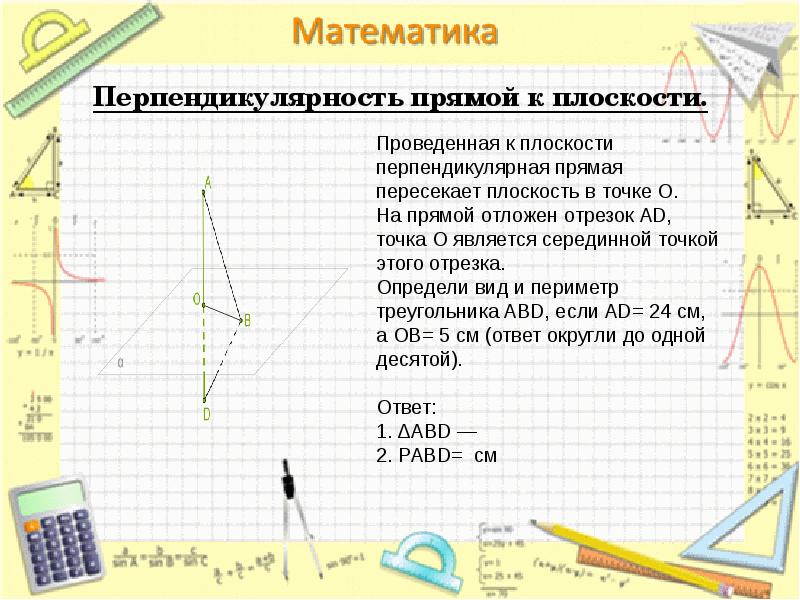
Перпендикулярность прямой к плоскости.

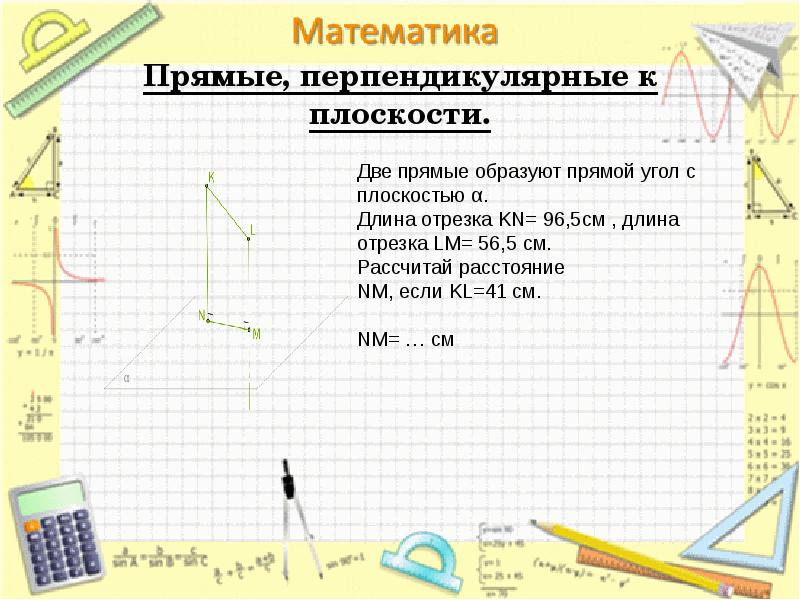
Прямые, перпендикулярные к плоскости.

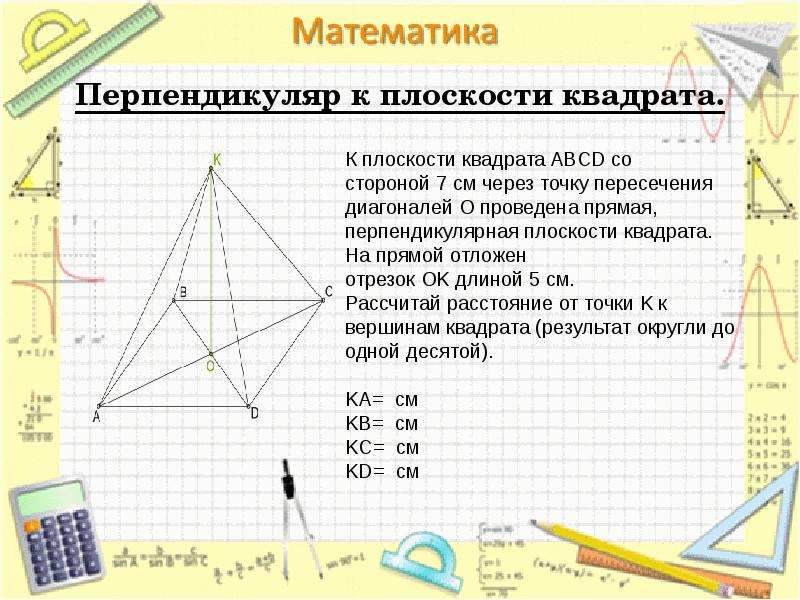
Перпендикуляр к плоскости квадрата.

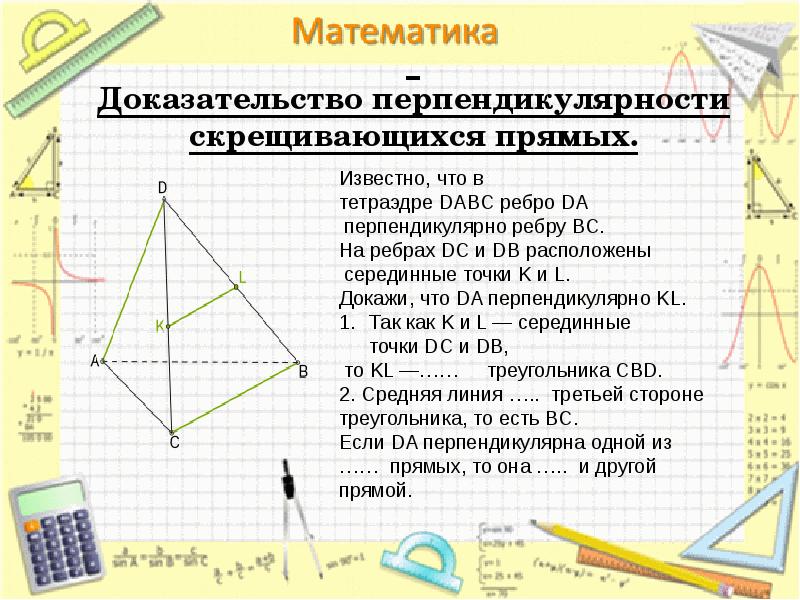
Доказательство перпендикулярности скрещивающихся прямых.

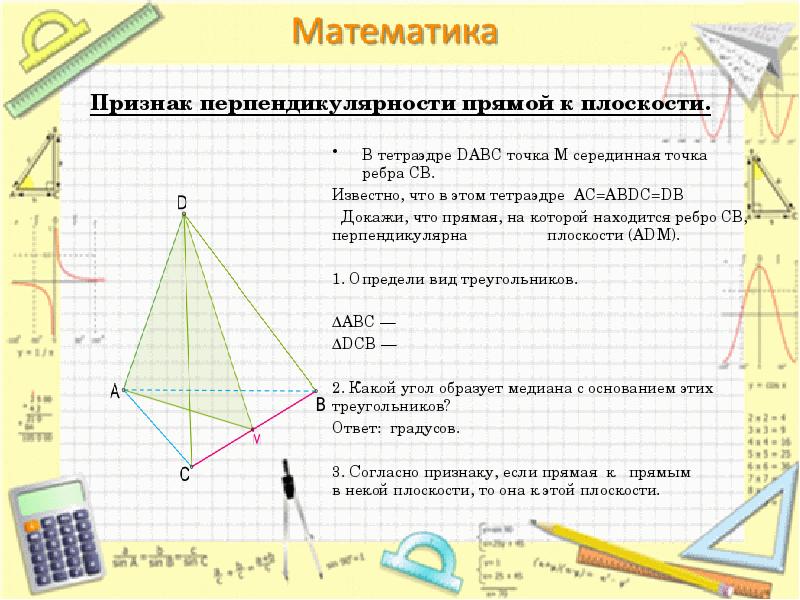
Признак перпендикулярности прямой к плоскости. В тетраэдре DABC точка M серединная точка ребра CB. Известно, что в этом тетраэдре AC=ABDC=DB Докажи, что прямая, на которой находится ребро CB, перпендикулярна плоскости (ADM).   1. Определи вид треугольников.   ΔABC —  ΔDCB —    2. Какой угол образует медиана с основанием этих треугольников? Ответ:  градусов.   3. Согласно признаку, если прямая  к   прямым в некой плоскости, то она к этой плоскости.

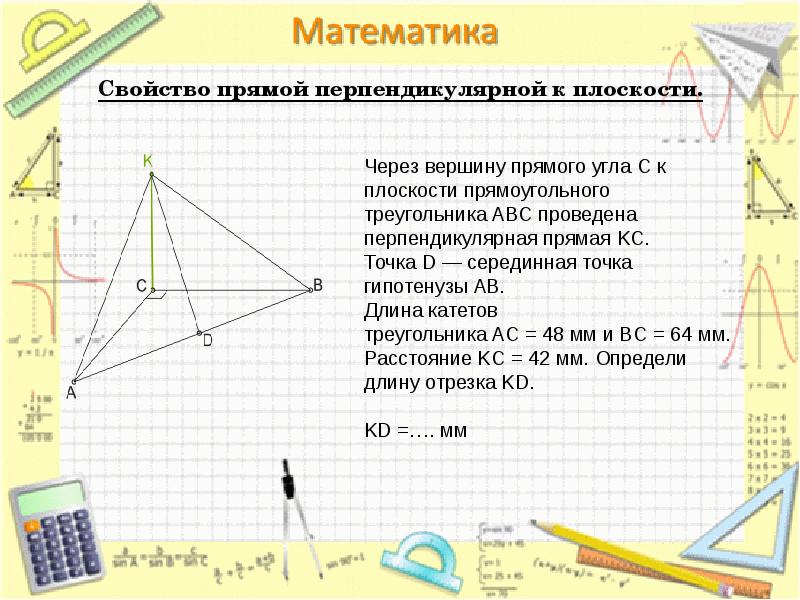
Свойство прямой перпендикулярной к плоскости.

(сложное) Доказательство от противного. Прямая d перпендикулярна плоскости α и прямой m, которая не лежит в плоскости α. Докажи, что прямая m параллельна плоскости α. 1. Согласно данной информации, если прямая не лежит в плоскости, она может или быть  …плоскости, или  … плоскость. 2. Допустим, что прямая m не ….., а  …..плоскость α. 3. Если прямая d по данной информации перпендикулярна плоскости α, то она …… каждой прямой в этой плоскости, в том числе и прямой, которая проведена через точки, в которых плоскость пересекает прямые d и m. 4. Мы имеем ситуацию, когда через одну точку к прямой d проведены две …… прямые.  5. Это противоречие, из чего следует, что прямая m…..  плоскости α, что и требовалось доказать.

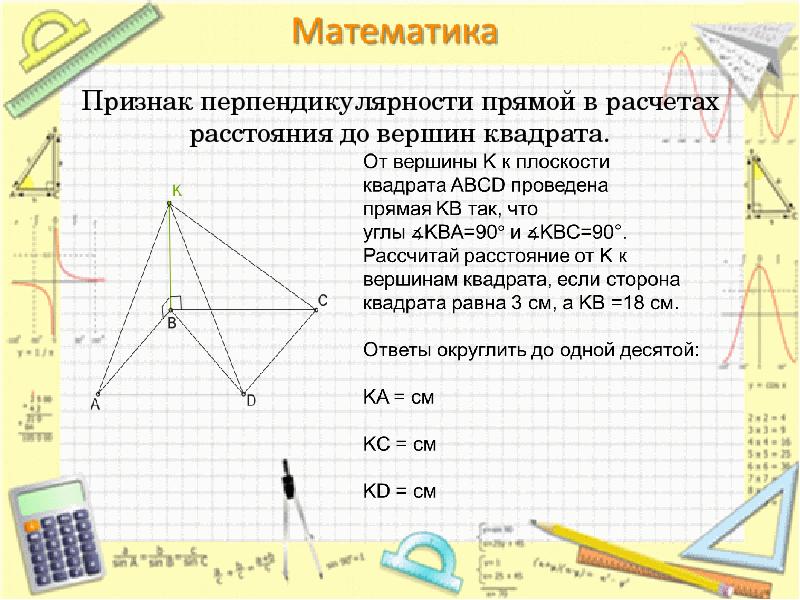
Признак перпендикулярности прямой в расчетах расстояния до вершин квадрата.

Домашнее задание П.15,16 Вопросы1,2 (стр.57) №116,118