ТЕОРИЯ ВЕРОЯТНОСТЕЙ презентация
Содержание
- 2. Любая точная наука изучает не сами явления, протекающие в природе, в
- 3. Задачи, исход которых нельзя предсказать с полной уверенностью, требуют изучения не
- 4. Статистические закономерности исследуются методами специальных математических дисциплин — теории вероятностей и
- 5. Элементы комбинаторики Упорядоченным называется множество, в котором указан порядок следования элементов.
- 6. Размещения из n элементов по k элементов Пусть некоторое множество А
- 7. Для числа размещений справедлива формула: Для числа размещений справедлива формула:
- 8. Перестановки из n элементов Размещение из n элементов по n называется
- 9. Сочетания из n элементов по k элементов Пусть задано множество, состоящее
- 10. Для числа сочетаний справедлива формула
- 11. Пример Для проведения экзамена создается комиссия из двух преподавателей. Сколько различных
- 12. Пример На втором курсе изучают 10 различных предметов. Сколькими способами можно
- 13. События и вероятность Эксперимент, испытание, опыт, процесс — это возникновение или
- 14. Среди событий отличают достоверное и невозможное события. Среди событий отличают
- 15. Примеры событий: выпадение орла при бросании монеты, выигрыш по облигации, увеличение
- 16. Любое событие А из пространства Любое событие А из пространства можно
- 17. Событие называется случайным, если оно может произойти, а может не произойти
- 18. События A, B, C, … называются попарно-несовместными, если любые два из
- 19. Несколько событий в данном опыте называются равновозможными, если ни одно из
- 20. Действия над событиями Суммой событий A и B называется событие C=A+B,
- 21. Разностью событий A и B называется событие C=A-B происходящее тогда
- 22. Понятие вероятности Под вероятностью события понимается некоторая числовая характеристика возможности наступления
- 23. Статистическое определение вероятности Пусть при проведении n испытаний некоторое событие
- 24. Классическое определение вероятности Классической схемой, или схемой случаев, называется испытание, при
- 25. Классической вероятностью события А называется отношение числа т элементарных событий, благо-приятствующих
- 26. Свойства вероятностей 1. Вероятность невозможного события равна нулю, т.е. 2.
- 27. Пример В коробке имеются 10 шаров, которые различаются только цветом. Среди
- 28. Пример В коробке 5 синих, 4 красных и 3 зеленых карандаша.
- 29. Геометрическое определение вероятности Геометрическое определение вероятности применяется в случае, когда
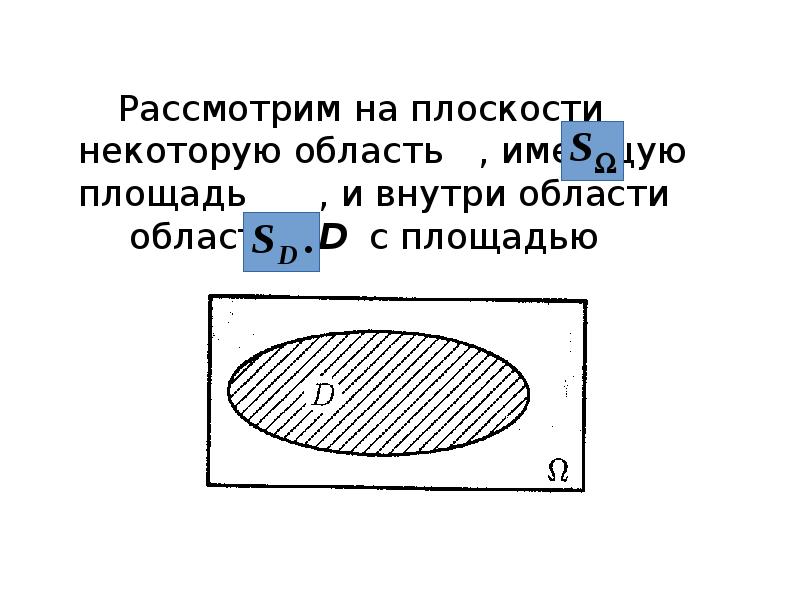
- 30. Рассмотрим на плоскости некоторую область , имеющую площадь , и внутри
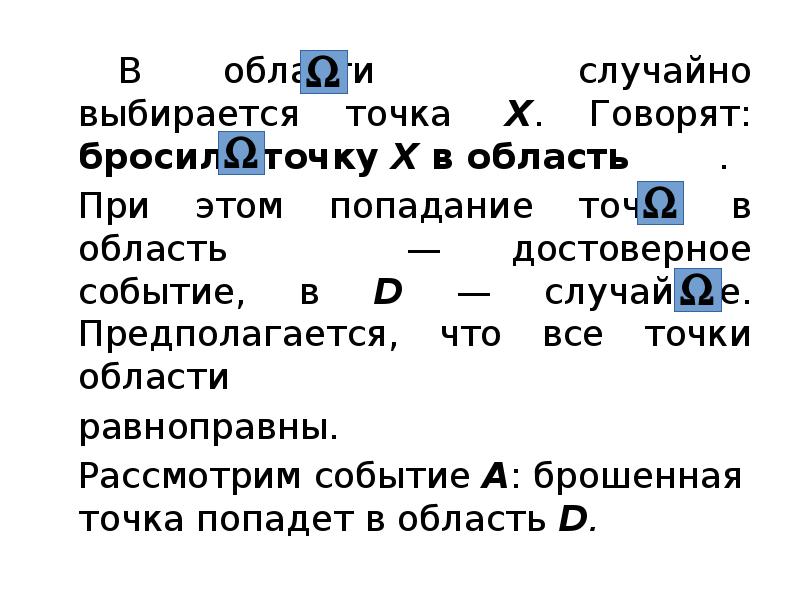
- 31. В области случайно выбирается точка X. Говорят: бросили точку X
- 32. Геометрической вероятностью события A называется отношение площади области D к площади
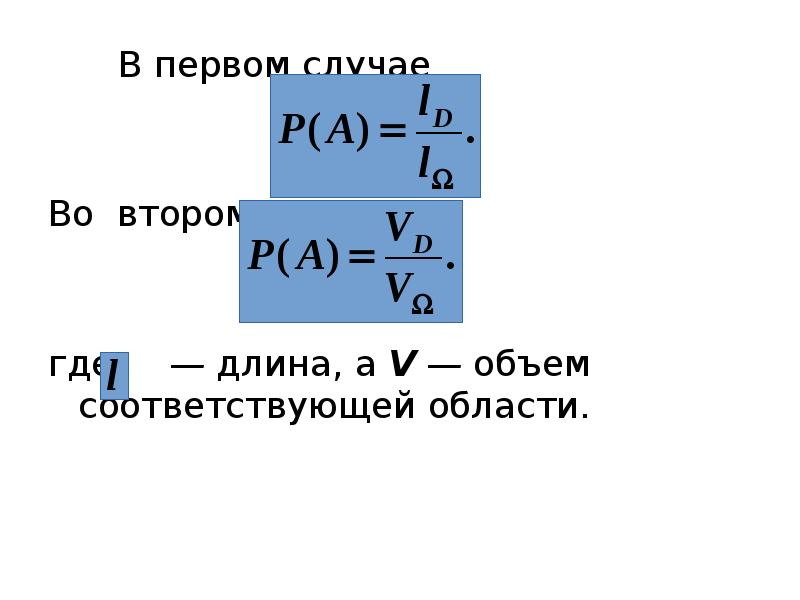
- 33. В первом случае В первом случае Во втором: где —
- 34. Геометрическая вероятность обладает всеми свойствами, присущими классическому (и другим) определению: Геометрическая
- 35. Пример После бури на участке между 40-м и 70-м километром телефонной
- 36. Скачать презентацию
































Слайды и текст этой презентации
Похожие презентации





























