Матрицы презентация
Содержание
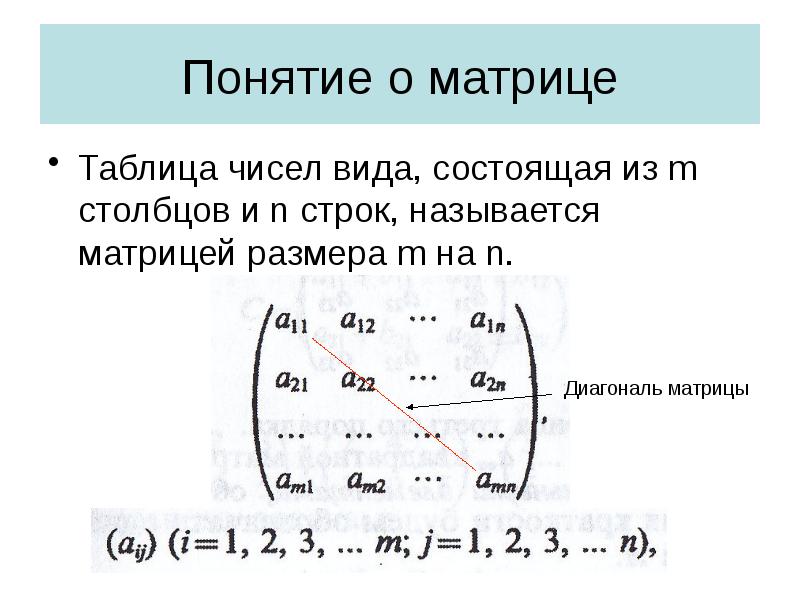
- 2. Понятие о матрице Таблица чисел вида, состоящая из m столбцов и
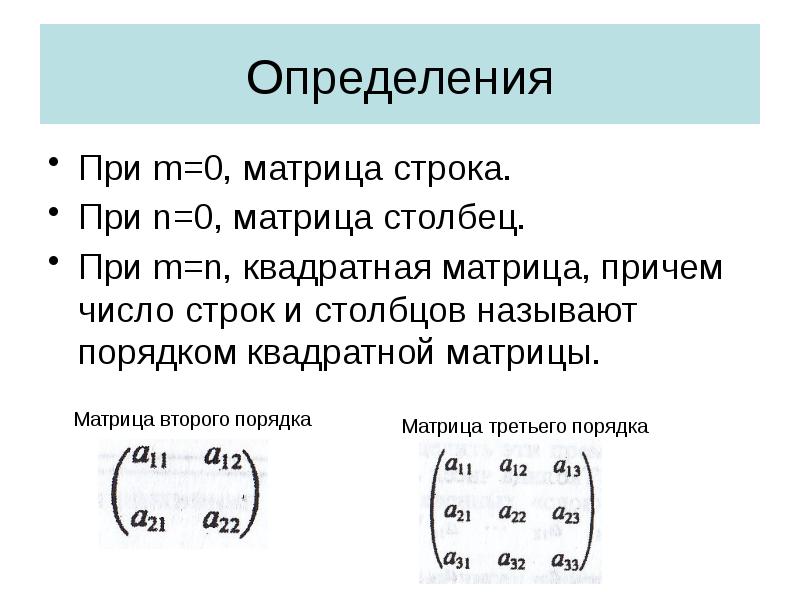
- 3. Определения При m=0, матрица строка. При n=0, матрица столбец. При m=n,
- 4. Равенство матриц Две матрицы А и В называют равными А=В, если
- 5. Сложение матриц Матрицы одинакового размера можно сложить. Суммой двух матриц А
- 6. Сложение матриц Сложение матриц подчиняется переместительному и сочетательному закону.
- 7. Вычитание матриц Разностью двух матриц А и В одинакового размера называется
- 8. Умножение матрицы на число Произведением матрицы А на число L называется
- 9. Умножение матриц Элемент матрицы произведения, находящийся на пересечении i-строки и k-столбца,
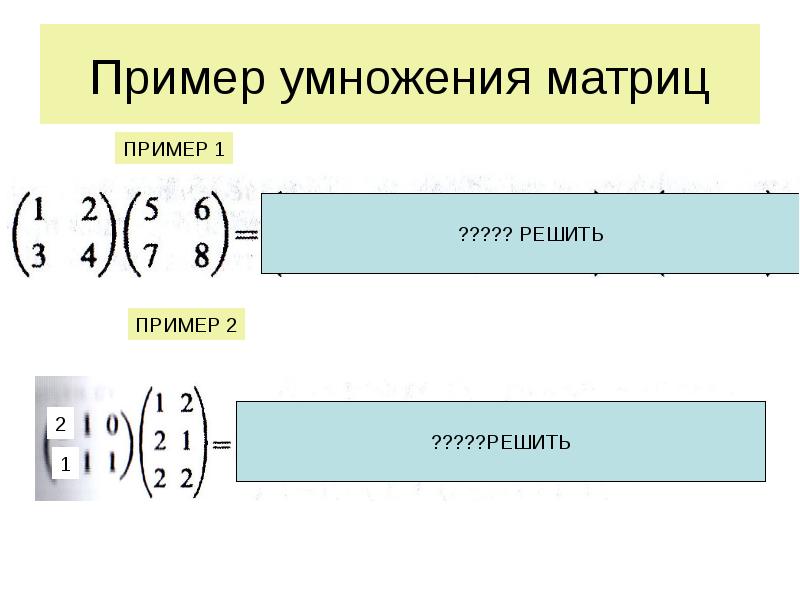
- 10. Пример умножения матриц
- 11. Пример умножения матриц
- 12. Пример 3
- 13. ПРИМЕР 3
- 14. ПРИМЕР 3
- 15. Особенность произведения матриц Известно, что произведение двух отличных от нуля чисел
- 16. Особенность произведения матриц
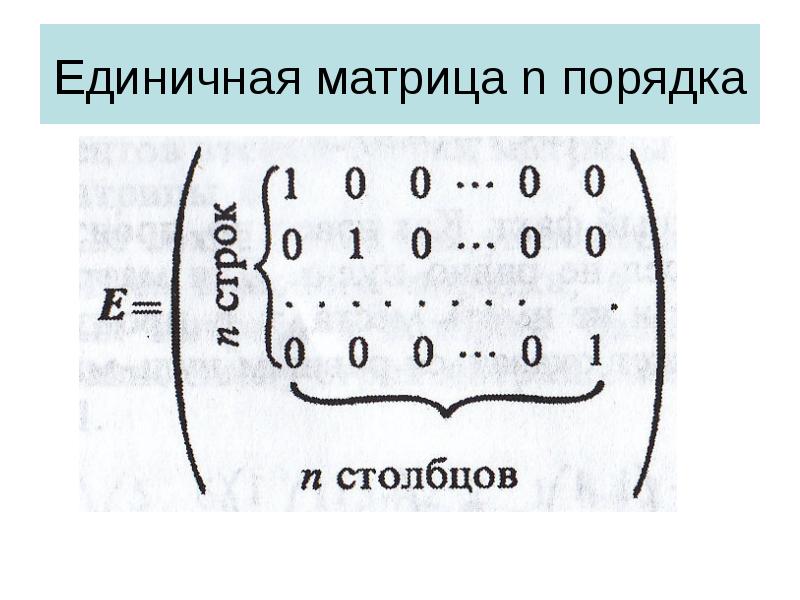
- 17. Свойство единичной матрицы Матрица вида Е – называется единичной матрицей. При
- 18. Единичная матрица n порядка
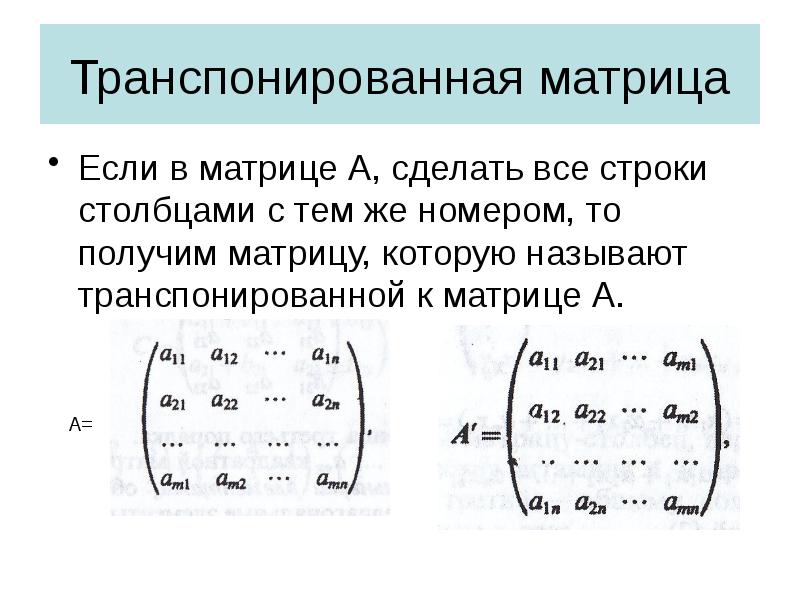
- 19. Транспонированная матрица Если в матрице А, сделать все строки столбцами с
- 20. Диагональная матрица Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных —
- 21. Определитель второго порядка Определителем второго порядка, соответствующим матрице А, называется число,
- 22. Пример вычисления определителя
- 23. Свойства определителя Величина определителя не меняется, если его строки заменить соответствующими
- 24. Определители третьего порядка Определителем третьего порядка, соответствующим матрице А, называется число
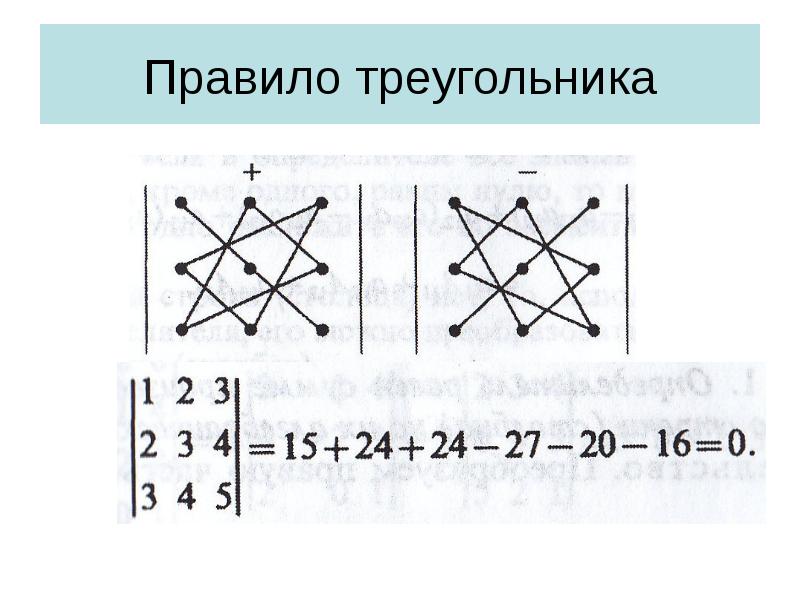
- 25. Правило треугольника
- 26. Свойства определителей третьего порядка Все свойства определителя второго порядка остаются справедливыми
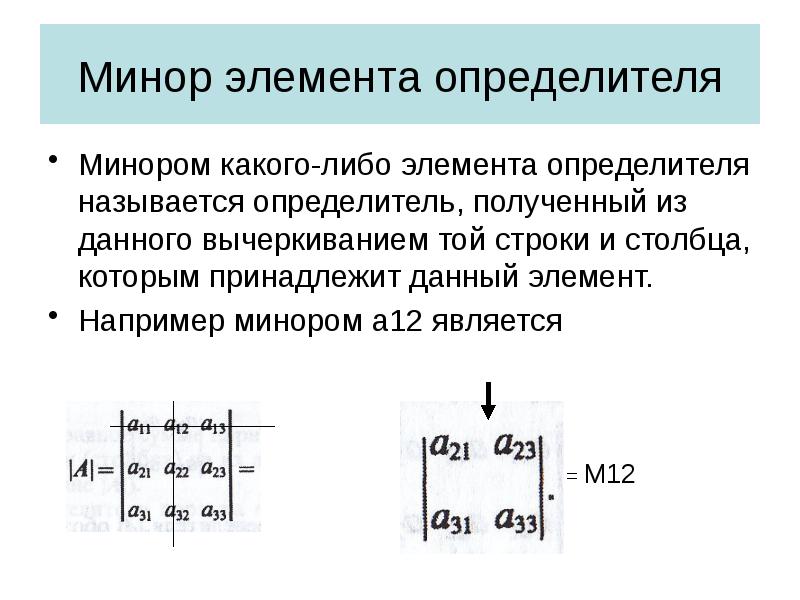
- 27. Минор элемента определителя Минором какого-либо элемента определителя называется определитель, полученный из
- 28. Алгебраическое дополнение элемента определителя Называется его минор взятый со знаком минус
- 29. Теорема Определитель равен сумме произведений элементов какой либо строки или столбца
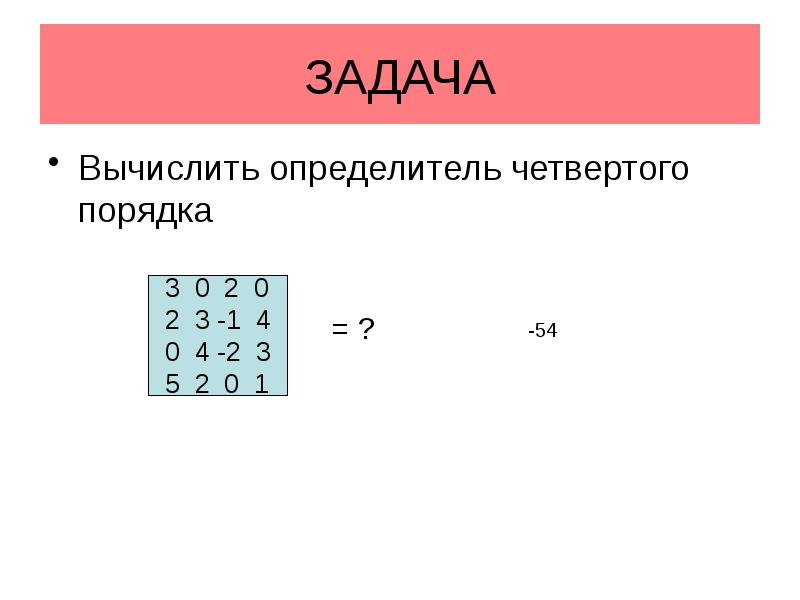
- 30. ЗАДАЧА Вычислить определитель четвертого порядка
- 31. Теорема Если А и В – квадратные матрицы одного порядка с
- 32. Обратная матрица Только для квадратных матриц, имеющих не нулевой определитель. Если
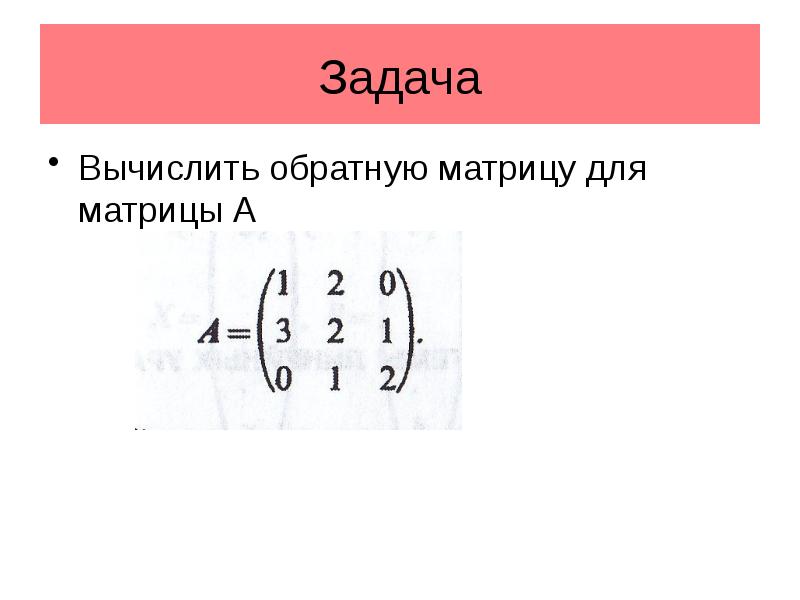
- 33. Задача Вычислить обратную матрицу для матрицы А
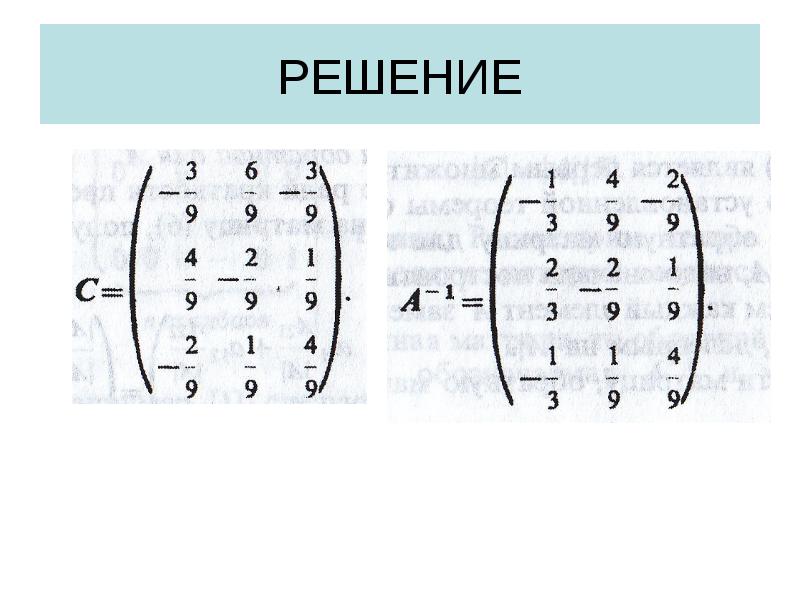
- 34. Решение
- 35. РЕШЕНИЕ
- 36. Скачать презентацию

























Слайды и текст этой презентации
Похожие презентации





























