Complex numbers презентация

Complex numbers Hanin Kirill, Gubenok Roman, Nesterov Michael – AM-28 Teacher Anna Valentinovna

Key words: Definition, equality, ordering, conjugate, addition and subtraction, multiplication, divison, modulus and argument, Pythagoras' theorem, Euler.

Definition A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is a solution of the equation x2 = −1. Because no real number  satisfies this equation, i is called an imaginary number. For the complex number a + bi, a is called the real part, and b is called the imaginary part. A complex number can be visually represented as a pair of numbers (a, b)  forming a vector on a diagram called an Argand diagram, representing the complex plane. "Re" is the real axis, "Im" is the imaginary axis, and i satisfies i2 = −1.

For example, the equation has no real solution, since the square of a real number cannot be negative. Complex numbers provide a solution to this problem. The idea is to extend the real numbers with an indeterminate i (sometimes called the imaginary unit) that is taken to satisfy the relation i2 = −1, so that solutions to equations like the preceding one can be found. In this case the solutions are −1 + 3*i and −1 – 3*i, as can be verified using the fact that i2 = −1:

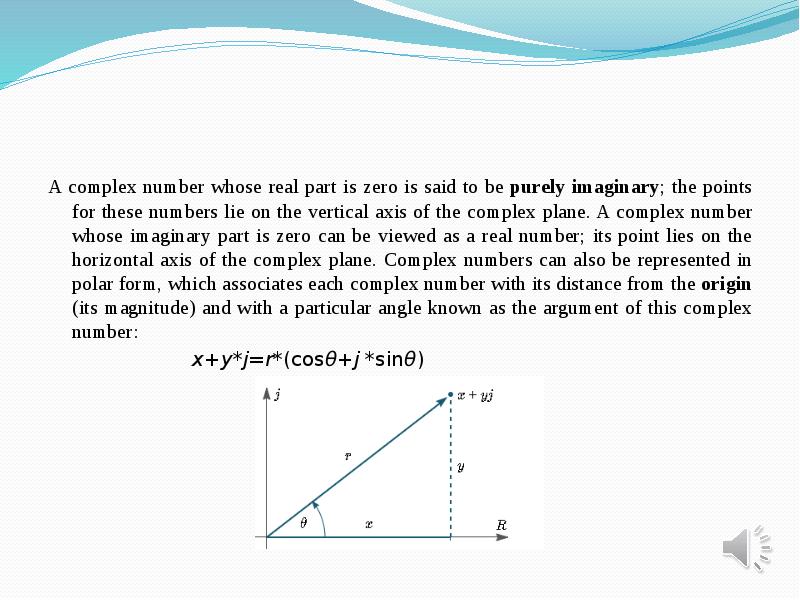
A complex number whose real part is zero is said to be purely imaginary; the points for these numbers lie on the vertical axis of the complex plane. A complex number whose imaginary part is zero can be viewed as a real number; its point lies on the horizontal axis of the complex plane. Complex numbers can also be represented in polar form, which associates each complex number with its distance from the origin (its magnitude) and with a particular angle known as the argument of this complex number: x+y*j=r*(cosθ+j *sinθ)

Some relations and operations Equality. Two complex numbers are equal if and only if both their real and imaginary parts are equal. That is, complex numbers z1  and z2 are equal if and only if Re(z1) = Re(z2) and Im(z1) = Im(z2 )Nonzero complex numbers written in polar form are equal if and only if they have the same magnitude and their arguments differ by an integer multiple of 2π.

Ordering. Since complex numbers are naturally thought of as existing on a two-dimensional plane, there is no natural linear ordering on the set of complex numbers. In fact, there is no linear ordering on the complex numbers that is compatible with addition and multiplication – the complex numbers cannot have the structure of an ordered field. This is because any square in an ordered field is at least 0, but i2 = −1. For example: but:

Conjugate. The complex conjugate of the complex number  z = x + y*i is given by x – y*i. It is denoted by either   or z*. This unary operation on complex numbers cannot be expressed by applying only their basic operations addition, subtraction, multiplication and division.   Geometrically,   is the reflection of z about the real axis. Conjugating twice gives the original complex number, which makes this operation an involution.

Addition and subtraction. Two complex numbers a and b are most easily added by separately adding their real and imaginary parts of the summands. That is to say: Similarly, subtraction can be performed as

Multiplication. Since the real part, the imaginary part, and the indeterminate i in a complex number are all considered as numbers in themselves, two complex numbers, given as z = x + y*I and w = u + v*i are multiplied under the rules of the distributive property the commutative properties and the defining property i2 = -1 in the following way:

Divison. Using the conjugation, the reciprocal of a nonzero complex number z = x + y*i can always be broken down to since nonzero implies that x2 + y2 is greater than zero. This can be used to express a division of an arbitrary complex number w = u + v*i by a non-zero complex number z as

Modulus and argument An alternative option for coordinates in the complex plane is the polar coordinate system that uses the distance of the point z from the origin (O), and the angle subtended between the positive real axis and the line segment Oz in a counterclockwise sense. This leads to the polar form of complex numbers. The absolute value (or modulus or magnitude) of a complex number z = x + y*i is If z is a real number (that is, if y = 0), then r = |x|. That is, the absolute value of a real number equals its absolute value as a complex number.

Pythagoras' theorem By Pythagoras' theorem, the absolute value of complex number is the distance to the origin of the point representing the complex number in the complex plane. In mathematics, the Pythagorean theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c.

The argument of z (in many applications referred to as the "phase" φ) is the angle of the radius Oz with the positive real axis, and is written as arg(z). As with the modulus, the argument can be found from the rectangular form x + y*i by applying the inverse tangent to the quotient of imaginary-by-real parts. By using a half-angle identity a single branch of the arctan suffices to cover the range of the arg-function, (−π, π], and avoids a more subtle case-by-case analysis

Normally, as given above, the principal value in the interval (−π, π] is chosen. Values in the range [0, 2π) are obtained by adding 2π if the value is negative. The value of φ is expressed in radians. It can increase by any integer multiple of 2π and still give the same angle, viewed as subtended by the rays of the positive real axis and from the origin through z. Hence, the arg function is sometimes considered as multivalued. The polar angle for the complex number 0 is indeterminate, but arbitrary choice of the polar angle 0 is common. The value of φ equals the result of atan2:

Together, r and φ give another way of representing complex numbers, the polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular coordinates from the polar form is done by the formula called trigonometric form Using Euler's formula this can be written as

Thanks for watching